7. Окрестности. Свойства окрестностей.
ε-окрестностью
точки
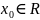называется интервал вида (
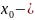ε,
ε ) =
(
,
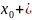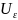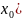ε>0
Окрестностью
точки
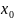называется
любое множество, содержащее некоторую
ε-окрестность этой точки.
ε-окрестностью
точки
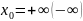называется интервал вида (ε,
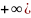
[ (ε,
+
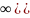
Свойства окрестностей.
1) Любая окрестность точки содержит эту точку
2) пересечение двух окрестностей точки снова является окрестностью этой точки.
Доказательство:
Рассмотрим
любу точку
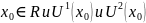
По определению
окрестности существует
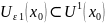и
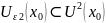
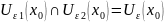– содержащая точку
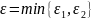
3) Свойство
отделимости. Есл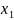и
и
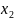– произвольные действительные числа
и различны => существует окрестность
U(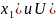
)
такие, что пересечение этих двух
окрестностей – не окрестность какой-либо
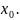U(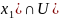
)
=
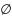
Доказательство:
и - два различных конечных числа. Пусть < => существует a такое, что:
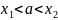
Возьмем
множество U(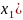
с правым концом a и U(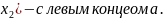
Их пересечение будет пусто множество.
8. Предельная точка множества. Основное определение предела функции.
Рассмотрим
множество
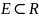
Точка a
называется предельной для множества
У, если в любой ее окрестности содержится
хотя бы одна точка из E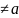
Теорема.
Если
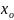– предельная для Е точка, то в любой ее
окрестности содержится бесконечное
количество точек из Е.
Доказательство: пусть – предельная для Е точка. Рассмотрим некоторую окрестность U( )
Предположим, что в U( ) содержится конечное число точек из E – x1 , x2 , x3 … xk
По свойству
3 окрестностей, существует u1(x0)
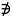x1,
u2(x0)
x2,
u3(x0)
x3,
… uk(x0)
xk.
Получается, что пересечение этих окрестностей – снова окрестность xo, не содержащее ни одну их точек x1.. xk. То есть, xo не является предельной для множества К.
Получаем противоречие – теорема доказана. Множество предельных для Е точек будем обозначать Е1
Определение предела 1
Пусть есть
функция F: x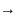
Y,
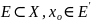
P
называется пределом функции f(x)
при x
на множестве Е, если для любой окрестности
p существует окрестность
точки
,
что как только х попадает в эту окрестность
(проколотую ) -
,
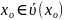как значение функции попадает в
окрестность точки p.
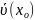– проколотая окрестность = U(
)\
{
}
9. Предел функции. Общие свойства предела (св.1 – св.3). Основное определение предела (определение 0 )
Число p R называется пределом функции f(x) при x , если значение функции становится как угодно близким к p лишь только x ( из области определения ) становится как угодно близким к
Определение предела 1
Пусть есть функция F: x Y,
P называется пределом функции f(x) при x на множестве Е, если для любой окрестности p существует окрестность точки , что как только х попадает в эту окрестность (проколотую ) - , как значение функции попадает в окрестность точки p.
– проколотая окрестность = U( )\ { }
Определение 2.
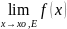= p
Число
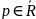называется
пределом функции f(x)
при
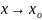на
множестве Е, если
:
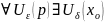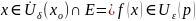
Пользуясь
определением 2 можно дать определение
предела через неравенства для конкретных
.
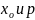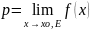, если
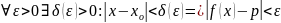
Например
для p =
,
:
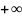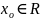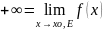, если
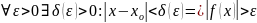
Свойства предела :
1)
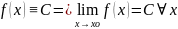
2) Если существует предел функции, то он единственный. Доказательство:
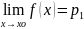(1) и
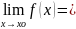
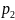(2)
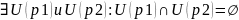
(1) =>
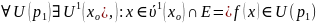
(2) =>
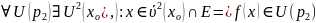
Тогда для
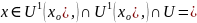
f(x)
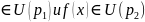=> не может быть, так как эти две
окрестности не пересекаются.
3) Пусть
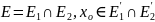
Тогда
существование предела
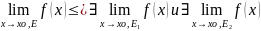и равенству этих трех пределов.