
- •А.А. Халафян
- •Лекция 1. Теории вероятностей. История возникновения. Классическое определение вероятности
- •Классическое определение вероятности
- •Лекция 2. Теоремы сложения и умножения вероятностей. Статистическое, геометрическое определение вероятности
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •Последовательность испытаний. Формула Бернулли
- •Лекция 3. Аксиоматическое построение теории вероятностей. Аксиоматика колмогорова
- •Лекция 4. Случайная величина. Функция распределения
- •Основные свойства функции распределения
- •X1 x2 … xn …, причём xn→-∞, n→∞.
- •Лекция 6. Интегральная теорема муавра–лапласа, теорема бернулли
- •Лекция 7. Непрерывные случайные величины
- •Свойства непрерывной случайной величины
- •Законы распределения непрерывных случайных величин Равномерное распределение
- •Экспоненциальное распределение
- •Нормальное распределение
- •Лекция 8. Понятие многомерной случайной величины
- •Аналогично закон распределения y имеет вид
- •Лекция 9. Функция распределения многомерной случайной величины
- •Плотность вероятностей двумерной случайной величины
- •Лекция 10. Свойства плотности вероятностей двумерной случайной величины
- •Лекция 11. Функции от случайных величин
- •Лекция 12. Теорема о плотности суммы двух случайных величин
- •Лекция 13. Распределения стьюдента, фишера .Числовые характеристики случайных величин
- •Числовые характеристики случайных величин
- •Свойства математического ожидания случайной величины
- •Лекция 14. Числовые характеристики случайных величин (продолжение)
- •Другие характеристики центра группирования случайной величины
- •Характеристики вариации случайной величины
- •Свойства дисперсии
- •Свойства среднеквадратического отклонения
- •Лекция 15. Вычисление дисперсии основных распределений
- •Лекция 16. Числовые характеристики меры связи случайных величин
- •Лекция 17. Предельные теоремы теории вероятностей. Неравенство чебышева. Закон больших чисел
- •Неравенство Чебышева
- •Закон больших чисел
- •Закон больших чисел для одинаково распределенных случайных величин
- •Закон больших чисел в форме Бернулли
- •Лекция 18. Центральная предельная теорема
- •Лекция 19. Математическая статистика. Предмет математической статистики. Вариационные ряды
- •Лекция 20. Средние величины. Показатели вариации
- •Свойства среднего арифметического
- •Показатели вариации (изменчивости) вариационного ряда
- •Свойства дисперсии
- •Статистическая выборка
- •Лекция 21. Оценка параметров генеральной совокупности
- •Лекция 22. Точечные и интервальные оценки параметров распределения Метод наибольшего правдоподобия
- •Метод моментов
- •Интервальная оценка
- •Лекция 23. Проверка статистических гипотез
- •Лекция 24. Проверка гипотезы о равенстве средних
- •Проверка гипотезы о равенстве дисперсий
- •Проверка гипотезы о законе распределения
- •Лекция 25. Элементы регрессионного и корреляционного анализов
- •Линеаризующие преобразования
- •Линейный множественный регрессионный анализ
- •Множественный корреляционный анализ
- •Библиографические ссылки
Лекция 6. Интегральная теорема муавра–лапласа, теорема бернулли
Для вычисления при больших n вероятности того, что число успехов в n испытаниях Бернулли находится между m1 и m2 , используется интегральная теорема Муавра–Лапласа.
Интегральная теорема Муавра – Лапласа. Если вероятность успеха в каждом испытании р, p(0;1) постоянна, то при n для любых a, b
 .
.
На
основании интегральной теоремы
Муавра–Лапласа для вычисления вероятности
события
![]() при больших n
и npq
9
используют приближенную формулу
при больших n
и npq
9
используют приближенную формулу
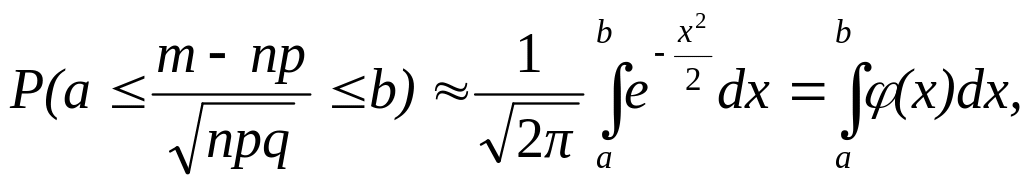
где
![]()
![]() .
.
Значения
![]() можно
найти, воспользовавшись таблицами
функции Лапласа
можно
найти, воспользовавшись таблицами
функции Лапласа
 ,
покажем это:
,
покажем это:
=
![]() ,
,
т.е. при больших n,
 Ф(b)
– Ф(а).
(1)
Ф(b)
– Ф(а).
(1)
Значения функции Лапласа приведены в таблицах для х 0. Для того, чтобы вычислить значения функции для отрицательных х, надо воспользоваться следующей теоремой.
Теорема. Ф(x) + Ф(-x) = 1.
Д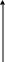 оказательство:
(x)
– чётная, так как (x)
= (-x).
Тогда
оказательство:
(x)
– чётная, так как (x)
= (-x).
Тогда
![]() (рис.1).
(рис.1).




-х х
Рис. 1
Следовательно, по интегральной теореме Муавра–Лапласа
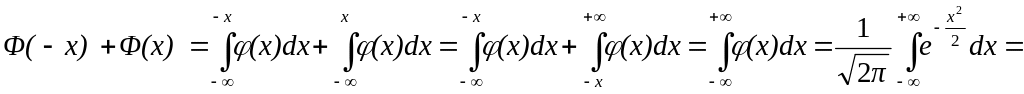
![]() .
.
В
некоторых источниках Ф(х)
определяется как
![]() .
.
В этом случае Ф(–x) = –Ф(x).
Событие
m1
m
m2
эквивалентно событию
![]() .
.
Поэтому, учитывая (1) для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено в пределах от m1 до m2 , можно использовать формулу
 ,
(2)
,
(2)
где
![]() ,
,
![]() .
.
Формула (2) хорошо работает, если n < 50. При больших значениях n лучше взять
![]() и
и
![]() .
.
Обозначим
через
вероятность того, что относительная
частота наступления успеха в n
испытаниях Бернулли отклонится от
вероятности успеха p
не более чем на
0, т.е.
![]() .
Покажем, что при достаточно больших n
с помощью интегральной теоремы
Муавра–Лапласа можно определить
вероятность .
.
Покажем, что при достаточно больших n
с помощью интегральной теоремы
Муавра–Лапласа можно определить
вероятность .

Следовательно, получим
![]() (3)
(3)
Формула содержит четыре параметра: n, p, , . Если известны любые 3, то можно определить четвертый параметр.
Если известны , , то n можно найти по формуле
![]() (4)
(4)
где
![]() –
это квадрат числа х,
такого, что Ф(х)
=
–
это квадрат числа х,
такого, что Ф(х)
=
![]() .
.
Теорема Бернулли. Пусть m – число успехов в n испытаниях по схеме Бернулли, вероятность успеха в каждом испытании равна p, тогда
>0,
![]() .
.
Доказательство.
![]()
![]()

Задача 1. Вероятность того, что случайно выбранный прибор нуждается в дополнительной настройке, равна 0,05. Если при выборочной проверке партии приборов обнаруживается, что не менее 6 % отобранных приборов нуждаются в регулировке, то вся партия возвращается для доработки. Определить вероятность того, что партия будет возвращена, если для контроля из партии выбрано 500 приборов.
Решение.
Партия
будет возвращена, если число отобранных
приборов, нуждающихся в настройке, будет
больше 6%, т.е. m1
= 500
6/100 = 30. Далее: p
= 0,05: q
= 0,95; np
= 25;
![]() 4,87.
За успех считаем, если прибор требует
дополнительной настройки.
4,87.
За успех считаем, если прибор требует
дополнительной настройки.
Применим интегральную теорему Муавра–Лапласа.

Задача 2. Определить, сколько надо отобрать изделий, чтобы с вероятностью 0,95 можно было утверждать, что относительная частота бракованных изделий будет отличаться от вероятности их появления не более чем на 0,01.
Решение. Для решения задачи выберем в качестве математической модели схему Бернулли и воспользуемся формулой (4). Надо найти такое n, чтобы выполнялось равенство (4), если = 0,01, = 0,95, вероятность р неизвестна.
Ф(х) = (1 + 0,95) / 2 = 0,975. По таблице приложения найдем, что х = 1,96. Тогда по формуле (4) найдем n = ¼ 1,962/0,012 = 9600.
