Лекция 3. Аксиоматическое построение теории вероятностей. Аксиоматика колмогорова

Классическое определение вероятности является весьма ограниченным. Ограниченность проявляется хотя бы в том, что события рассматриваются равновозможные, дискретные, число которых конечно. Рассмотрим, например, стрельбу по мишени. Если нас интересует только сам факт попадания по мишени, то элементарными исходами служат ω₁=1 и ω₂ = 0. Если нас интересует попадание в различные области мишени, то элементарными событиями могут быть ω₁₀ = 10, ω₉ = 9,… ω₀ = 0. В обоих случаях вероятности элементарных событий не одинаковы. Если нас интересует, в какую конкретно точку мишени попал стрелок, то произвольный элементарный исход ω = {X, Y} – представляет координаты точки попадания, а множество элементарных событий – это множество точек плоскости. Число точек плоскости не конечно и даже несчетно. Поэтому нужно так определить вероятность, чтобы это определение было одинаково пригодным для объектов различной природы.

При классическом определении вероятности в качестве события рассматривалось любое подмножество конечного множества элементарных событий  и вероятность события определялась как сумма вероятностей входящих в него элементарных событий. Если же  непрерывно, то имеет место континуум элементарных исходов. Попытка считать событием любое подмножество непрерывного множества  сопряжена с большими трудностями.

Поэтому в общем случае приходится иметь дело не со всеми подмножествами , а лишь с определенным классом, замкнутым относительно операций объединения и пересечения.

Определение 1. Класс подмножеств из , замкнутый относительно операций объединения, дополнения и пересечения, а также содержащий множества , , называется полем.

Будем обозначать поле буквой S. Минимальное поле состоит из полного и пустого множества S₀ = {, }. Другим примером поля событий служит класс из четырех событий S₁ = {, , А , }. Доказать самостоятельно.

Определение 2. Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами:

аксиома 1. Для любого события А  S, Р(А)  0;

аксиома 2. Вероятность достоверного события равна единице, P(Ω)=1;

аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий, т.е.

если АS, BS, А∩B = , то P(АB) = P(А+B) = P(А) +P(B).

Во многих случаях выполнение аксиомы 3 требуется в расширенном варианте, а именно, аксиома 3 постулирует сложение вероятностей для конечного числа несовместных событий, в то время как в расширенном варианте речь идет о счетном числе несовместных событий –

аксиома 3'. Если А_i  S, А_i ∩ А_j = ,  i ≠ j , то .

Определение 3. Набор объектов {Ω,S,P} называется вероятностным пространством, где Ω – множество всех элементарных событий, S – поле, P – вероятность, определенная на поле S.

В лекции 2 формула условной вероятности (4) была выведена на основе классического определения вероятности, для общего случая эта формула является определением условной вероятности.

Определение 4. Условная вероятность наступления события А при условии В равна

P(a/b) = Р(АВ)/Р(В) = Р(АВ)/Р(В).

Определение 5. Событие А не зависит от события В, если

Р(А/В) = Р(А).

Теорема 1. Независимость событий взаимна, т.е. если событие А не зависит от В, то и событие В не зависит от А.

Доказательство.

Р(В/А) = Р(ВА)/Р(А) = Р(АВ)/Р(А) = P(a/b)Р(В)/Р(А) = Р(А)Р(В)/Р(А) = Р(В).

Из определения 4 вытекают формулы умножения вероятностей для зависимых и независимых событий.

Следствие 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

P(A₁A₂… A_n) = P(A₁)P_A1(A₂)P_A1A2(A₃)… P_{A1A2… An-1}(A_n).

Определение 6. События A_1, A_2, …, A_n независимы в совокупности, если независимы любые два из них и независимы любое из этих событий и любые комбинации (произведения) остальных событий.

Следствие 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

P(A₁A₂… A_n) = P(A₁)P(A₂)… P(A_n).

Доказательство.

P(A₁A₂… A_n) = P(A₁·A₂… A_n) = P(A₁)P(A₂… A_n).=…= P(A₁)P(A₂)… P(A_n).

Определение 7. Событие А₁,А₂,… А_n образуют полную группу событий, если они попарно несовместны (А_i∩А_j = Ø, для любого i ≠ j) и в совокупности образуют Ω, т.е. .

Теорема 2. Если события А_1,A₂,… А_n образуют полную группу событий, Р(А_i)  0 (так как не будет определено P(B/A_i)), то вероятность некоторого события B  S определяется, как сумма произведений безусловных вероятностей наступления события А_i на условные вероятности наступления события B, т.е.

. (1)

Доказательство. Так как события А_i попарно несовместны, то их пересечение с событием B также попарно несовместны, т.е. B∩А_i и B∩А_j – несовместны при i  j. Используя свойство дистрибутивности ((А_i)В = (А_iВ)), событие B можно представить как . Воспользуемся аксиомой сложения 3 и формулой умножения вероятностей, получим

.

Формула (1) называется формула полной вероятности.

Из формулы полной вероятности легко получить формулу Байеса, при дополнительном предположении, что P(B)>0

,

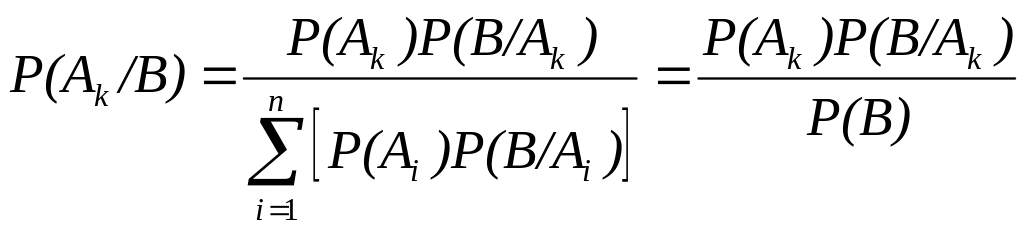где k = 1, 2, …, n.

Доказательство. P(А_k/B) = P(А_k ∩ B)/P(B)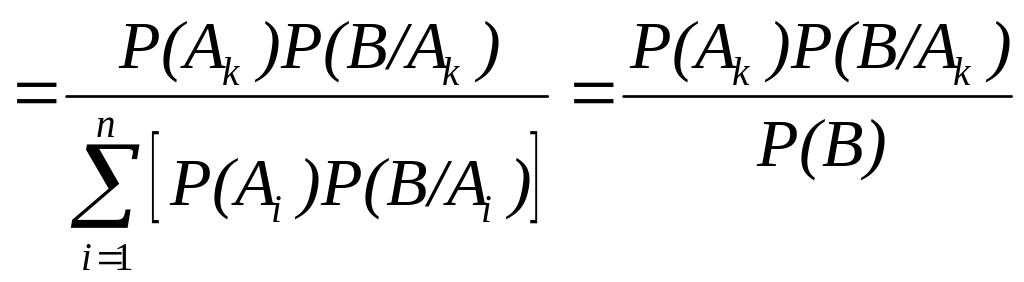

Вероятности событий P(А_i ), i =1, 2, …, n называются априорными вероятностями, т.е. вероятностями событий до выполнения опыта, а условные вероятности этих событий P(А_k/B), называются апостериорными вероятностями, т.е. уточненными в результате опыта, исходом которого послужило появление события В.

Задача. В торговую фирму поступили сотовые телефоны последних моделей от трех производителей Alcatel, Siemens, Motorola в соотношении 1 : 4 : 5. Практика показала, что телефоны, поступившие от 1-го, 2-го, 3-го производителя, не потребуют ремонта в течение гарантийного срока соответственно в 98 %, 88 % и 92 % случаев. Найти вероятность того, что поступивший в продажу телефон не потребует ремонта в течение гарантийного срока, проданный телефон потребовал ремонта в течение гарантийного срока, от какого производителя вероятнее всего поступил телефон.