Множественный корреляционный анализ

Во множественной ситуации вычисляют два типа коэффициентов корреляции:

– r_yxj – коэффициенты, показывающие тесноту связи j-го фактора x_j и функции отклика у;

– – коэффициенты, определяющие тесноту связи между фактором x_j и фактором x_m.

Введем обозначения

Тогда коэффициенты корреляции можно вычислить по формулам 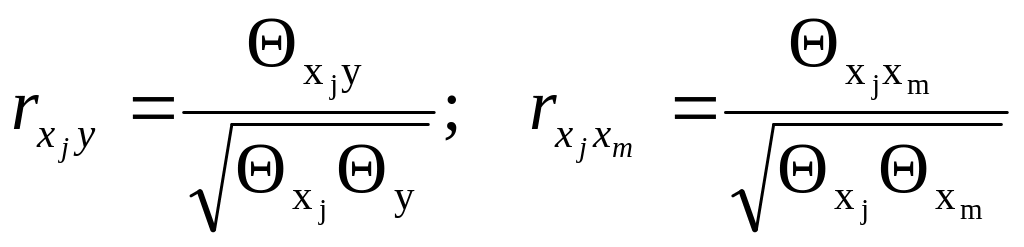(16)

. (16)

Если один из коэффициентов окажется равным единице, то это означает, что факторы x_j и x_m функционально связаны между собой, и тогда целесообразно один из них исключить из рассмотрения, причем оставляют тот фактор, у которого коэффициент r_yxj больше.

После вычисления всех парных коэффициентов корреляции и исключения из рассмотрения того или иного фактора, можно построить матрицу коэффициентов корреляции вида

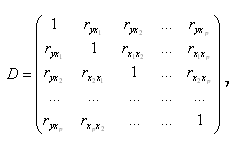
Используя данную матрицу, можно вычислить частные коэффициенты корреляции, которые показывают степень влияния одного из факторов х_i на функцию отклика, когда остальные факторы закреплены на постоянном уровне. Частные коэффициенты корреляции вычисляется по следующей формуле:

,

где D_1j – определитель матрицы, образованный из матрицы D вычеркиванием 1-й строки и j-го столбца. Определители D₁₁ и D_jj вычисляются аналогично.

Для изучения тесноты связи между функцией отклика у и несколькими факторами х₁, х₂ ,…, х_к используют коэффициент множественной корреляции R

.

После вычисления значений приведенных ранее коэффициентов корреляции необходимо проверить их статистическую значимость при помощи критериев Фишера и Стьюдента.

Библиографические ссылки

1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и мате-

матическая статистика. М.: Высшая Школа, 1991.

2. Елисеева И.И., Князевский В.С., Ниворожкина Л.И., Морозова З.А. Теория статистики с основами теории вероятностей. М.: Юнити, 2001.

3. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.: Мир, 1990.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2001

5. Смирнов Н.В. Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука,1969.

6. Статистические методы построения эмпирических формул. М.: Высшая Школа, 1988.

ОГЛАВЛЕНИЕ

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ 3

ЛЕКЦИЯ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. СТАТИСТИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ 8

ЛЕКЦИЯ 3. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АКСИОМАТИКА КОЛМОГОРОВА 13

ЛЕКЦИЯ 4. СЛУЧАЙНАЯ ВЕЛИЧИНА. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ 16

ЛЕКЦИЯ 5. РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 21

ЛЕКЦИЯ 6. ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА–ЛАПЛАСА, ТЕОРЕМА БЕРНУЛЛИ 25

ЛЕКЦИЯ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 28

ЛЕКЦИЯ 8. ПОНЯТИЕ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 34

ЛЕКЦИЯ 9. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 38

ЛЕКЦИЯ 10. СВОЙСТВА ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 42

ЛЕКЦИЯ 11. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН 46

ЛЕКЦИЯ 12. ТЕОРЕМА О ПЛОТНОСТИ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН 50

ЛЕКЦИЯ 13. РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА, ФИШЕРА .ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН 55

ЛЕКЦИЯ 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН (продолжение) 59

ЛЕКЦИЯ 15. ВЫЧИСЛЕНИЕ ДИСПЕРСИИ ОСНОВНЫХ РАСПРЕДЕЛЕНИЙ 64

ЛЕКЦИЯ 16. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МЕРЫ СВЯЗИ СЛУЧАЙНЫХ ВЕЛИЧИН 68

ЛЕКЦИЯ 17. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. НЕРАВЕНСТВО ЧЕБЫШЕВА. ЗАКОН БОЛЬШИХ ЧИСЕЛ 73

ЛЕКЦИЯ 18. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 76

ЛЕКЦИЯ 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ВАРИАЦИОННЫЕ РЯДЫ 80

ЛЕКЦИЯ 20. СРЕДНИЕ ВЕЛИЧИНЫ. ПОКАЗАТЕЛИ ВАРИАЦИИ 84

ЛЕКЦИЯ 21. ОЦЕНКА ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ 88

ЛЕКЦИЯ 22. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ 91

ЛЕКЦИЯ 23. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 95

ЛЕКЦИЯ 24. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ 99

ЛЕКЦИЯ 25. ЭЛЕМЕНТЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ 102

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ 109

111