
- •А.А. Халафян
- •Лекция 1. Теории вероятностей. История возникновения. Классическое определение вероятности
- •Классическое определение вероятности
- •Лекция 2. Теоремы сложения и умножения вероятностей. Статистическое, геометрическое определение вероятности
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •Последовательность испытаний. Формула Бернулли
- •Лекция 3. Аксиоматическое построение теории вероятностей. Аксиоматика колмогорова
- •Лекция 4. Случайная величина. Функция распределения
- •Основные свойства функции распределения
- •X1 x2 … xn …, причём xn→-∞, n→∞.
- •Лекция 6. Интегральная теорема муавра–лапласа, теорема бернулли
- •Лекция 7. Непрерывные случайные величины
- •Свойства непрерывной случайной величины
- •Законы распределения непрерывных случайных величин Равномерное распределение
- •Экспоненциальное распределение
- •Нормальное распределение
- •Лекция 8. Понятие многомерной случайной величины
- •Аналогично закон распределения y имеет вид
- •Лекция 9. Функция распределения многомерной случайной величины
- •Плотность вероятностей двумерной случайной величины
- •Лекция 10. Свойства плотности вероятностей двумерной случайной величины
- •Лекция 11. Функции от случайных величин
- •Лекция 12. Теорема о плотности суммы двух случайных величин
- •Лекция 13. Распределения стьюдента, фишера .Числовые характеристики случайных величин
- •Числовые характеристики случайных величин
- •Свойства математического ожидания случайной величины
- •Лекция 14. Числовые характеристики случайных величин (продолжение)
- •Другие характеристики центра группирования случайной величины
- •Характеристики вариации случайной величины
- •Свойства дисперсии
- •Свойства среднеквадратического отклонения
- •Лекция 15. Вычисление дисперсии основных распределений
- •Лекция 16. Числовые характеристики меры связи случайных величин
- •Лекция 17. Предельные теоремы теории вероятностей. Неравенство чебышева. Закон больших чисел
- •Неравенство Чебышева
- •Закон больших чисел
- •Закон больших чисел для одинаково распределенных случайных величин
- •Закон больших чисел в форме Бернулли
- •Лекция 18. Центральная предельная теорема
- •Лекция 19. Математическая статистика. Предмет математической статистики. Вариационные ряды
- •Лекция 20. Средние величины. Показатели вариации
- •Свойства среднего арифметического
- •Показатели вариации (изменчивости) вариационного ряда
- •Свойства дисперсии
- •Статистическая выборка
- •Лекция 21. Оценка параметров генеральной совокупности
- •Лекция 22. Точечные и интервальные оценки параметров распределения Метод наибольшего правдоподобия
- •Метод моментов
- •Интервальная оценка
- •Лекция 23. Проверка статистических гипотез
- •Лекция 24. Проверка гипотезы о равенстве средних
- •Проверка гипотезы о равенстве дисперсий
- •Проверка гипотезы о законе распределения
- •Лекция 25. Элементы регрессионного и корреляционного анализов
- •Линеаризующие преобразования
- •Линейный множественный регрессионный анализ
- •Множественный корреляционный анализ
- •Библиографические ссылки
Лекция 25. Элементы регрессионного и корреляционного анализов
К наиболее простым зависимостям тапа Y = f(X) (такие зависимости в литературе еще называют парными) относится подавляющее большинство формул, используемых в естественнонаучных и технических дисциплинах. Такие формулы, как правило, строятся по результатам экспериментов, применяя метод наименьших квадратов. Однако только сейчас с использованием вычислительной техники стало возможным строить парные зависимости оптимальной (в смысле адекватности) формы.
Пусть имеется n пар наблюдений значений зависимой переменной yi – функции отклика, полученных при фиксированных значениях независимой переменной xi – фактора.
xi |
x1 |
x2 |
… |
xn |
yi |
y1 |
y2 |
… |
yn |
Пары (xi, yi) на плоскости можно представить в виде точек с координатами (xi ,yi) (рис.1).
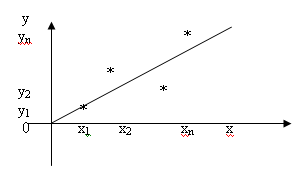
Рис.1
Задача
регрессионного анализа состоит в том,
чтобы, зная положение точек на плоскости,
так провести линию регрессии, чтобы
сумма квадратов отклонений
![]() вдоль оси 0Y
этих точек от проведенной линии была
минимальной. Для проведения регрессионного
анализа к выдвигаемой гипотезе (к форме
уравнения регрессии) выдвигается
требование, чтобы это уравнение было
линейным по параметрам или допускало
линеаризацию. Рассмотрим
сначала процедуру построения линейной
зависимости между фактором и откликом.
вдоль оси 0Y
этих точек от проведенной линии была
минимальной. Для проведения регрессионного
анализа к выдвигаемой гипотезе (к форме
уравнения регрессии) выдвигается
требование, чтобы это уравнение было
линейным по параметрам или допускало
линеаризацию. Рассмотрим
сначала процедуру построения линейной
зависимости между фактором и откликом.
Уравнение
прямой линии на плоскости имеет вид
![]() ,
где
,
где
![]() и
и
![]() – неизвестные постоянные. Тогда задачу
метода наименьших квадратов можно
сформулировать следующим образом –
минимизировать функционал U
по параметрам
и
– неизвестные постоянные. Тогда задачу
метода наименьших квадратов можно
сформулировать следующим образом –
минимизировать функционал U
по параметрам
и
![]() .
(1)
.
(1)
Решение задачи сводится к вычислению значений параметров и , доставляющих функционалу (1) минимальное значение. Необходимое условие экстремума запишем в виде системы (2)
![]() .
(2)
.
(2)
После нахождения производных получим так называемую систему нормальных уравнений (3)
![]() .
(3)
.
(3)
Для нахождения решения системы можно воспользоваться соотношениями (4)
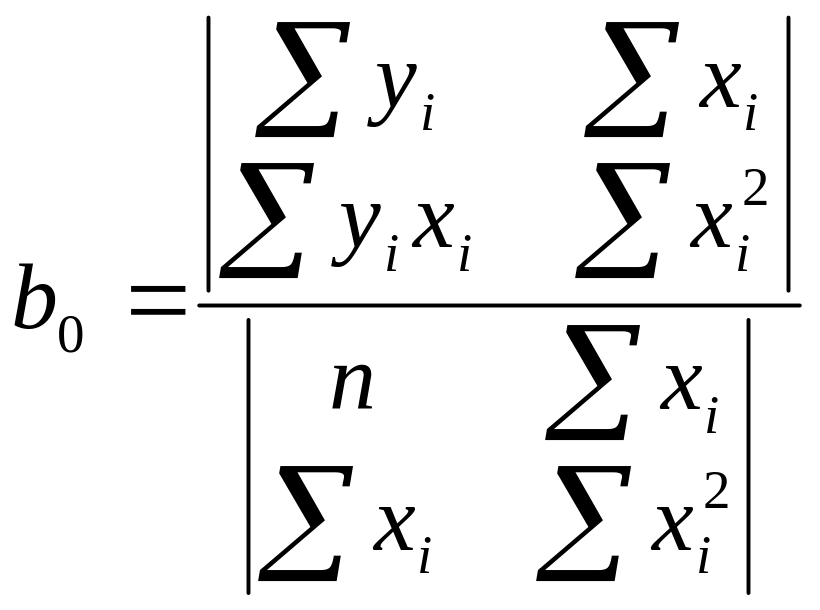 и
и
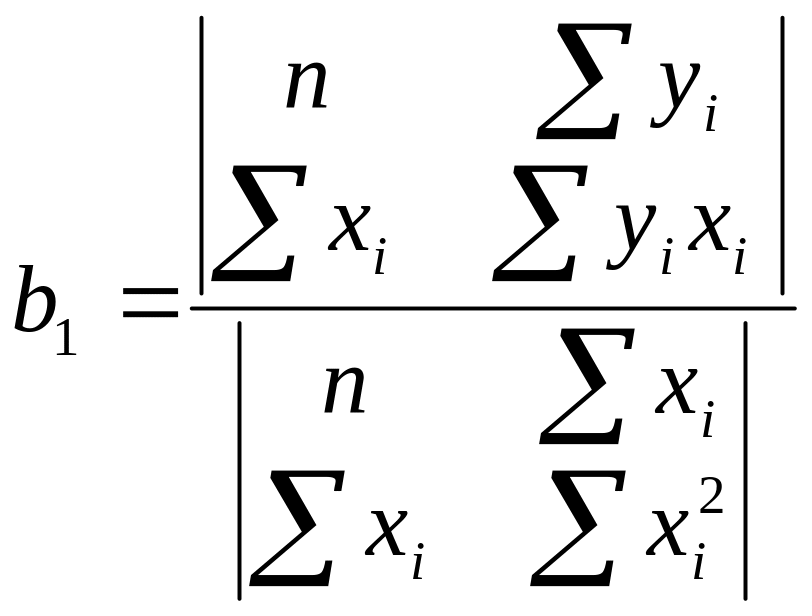 .
(4)
.
(4)
В
общем случае между X
и Y
может быть два вида связи – функциональная
и стохастическая. Первая имеет место,
если точки наблюдения эксперимента
расположены точно на линии регрессии.
При наличии погрешностей измерения –
связь стохастическая. Для функциональной
связи понятие корреляции r
не имеет смысла (коэффициент корреляции
равен 1 при линейной зависимости). Для
стохастической связи вычисление
корреляции между X
и Y
и его оценка – важная статистическая
процедура, которая позволяет судить о
тесноте связи между X
и Y.
Коэффициент корреляции r
может изменяться от –1 до +1. Чем ближе
r
к единице, тем связь между откликом и
фактором теснее. Если X
и Y
имеют нормальное распределение, то
равенство r
нулю означает независимость X
и Y.
X
и Y
имеют две линии регрессии. Одна определяет
зависимость Y
от X,
а вторая – зависимость X
от Y.
Прямые регрессии пересекаются в «центре
тяжести» (![]() )
и образуют «ножницы». Чем уже «ножницы»,
тем ближе стохастическая связь к
функциональной. Это означает, что
уравнение регрессии
)
и образуют «ножницы». Чем уже «ножницы»,
тем ближе стохастическая связь к
функциональной. Это означает, что
уравнение регрессии
![]() не является
алгебраическим, из которого можно
выразить X
через Y.
не является
алгебраическим, из которого можно
выразить X
через Y.
Коэффициент парной корреляции можно определить по формуле (5)
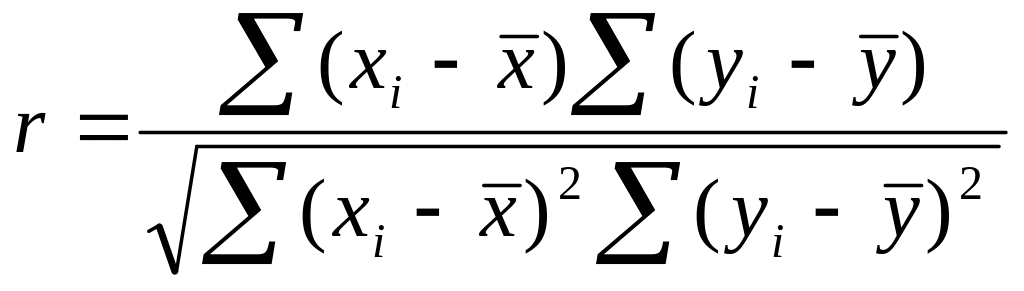 ,
(5)
,
(5)
где и – выборочные средние.
После определения коэффициентов уравнения регрессии и коэффициента корреляции необходимо оценить их статистическую значимость.
Статистическую значимость уравнения регрессии определяют с использованием критерия Фишера. Вычисляют статистику F-критерия по следующему соотношению (6):
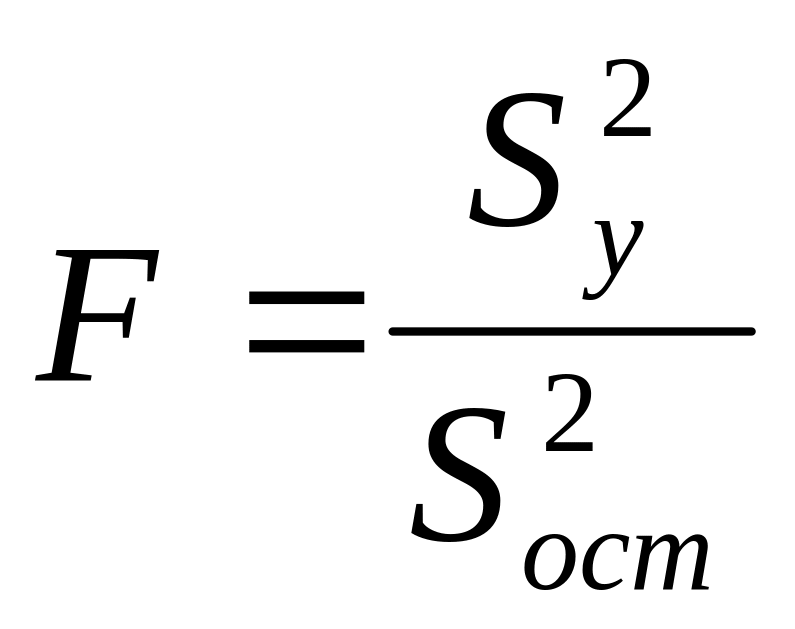 ,
(6)
,
(6)
где
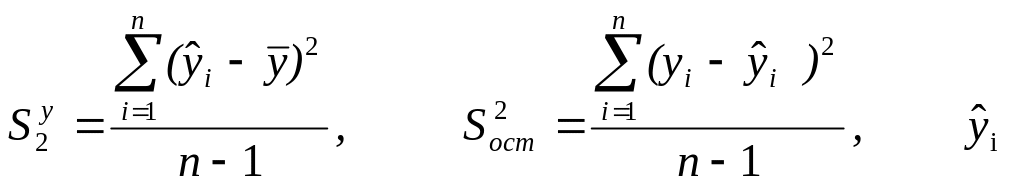
![]() .
.
Далее по таблице приложения находят табличное значение F-критерия при уровне значимости и степенями свободы n – 1, n – 2.
Если F < F(, n – 1, n – 2), то это означает, что уравнение регрессии статистически незначимо и неадекватно описывает результаты эксперимента; в противном случае уравнение регрессии статистически значимо. F-критерий показывает во сколько раз уравнение регрессии предсказывает результаты экспериментов лучше, чем среднее .
Для оценки статистической значимости r используется критерий Стьюдента:
![]() (7)
(7)
Вычисленное
по формуле (7)
![]() сравнивают с табличным – t(n
– 2, ),
если
> t(n
– 2,
),
то нуль гипотезу H0:
r
= 0 отклоняют, т.е. найденное r
статистически значимо отличается от
нуля.
сравнивают с табличным – t(n
– 2, ),
если
> t(n
– 2,
),
то нуль гипотезу H0:
r
= 0 отклоняют, т.е. найденное r
статистически значимо отличается от
нуля.
Статистическую значимость коэффициентов регрессии и также определяют при помощи критерия Стьюдента.
Адекватность модели можно оценить также при помощи коэффициента детерминации:
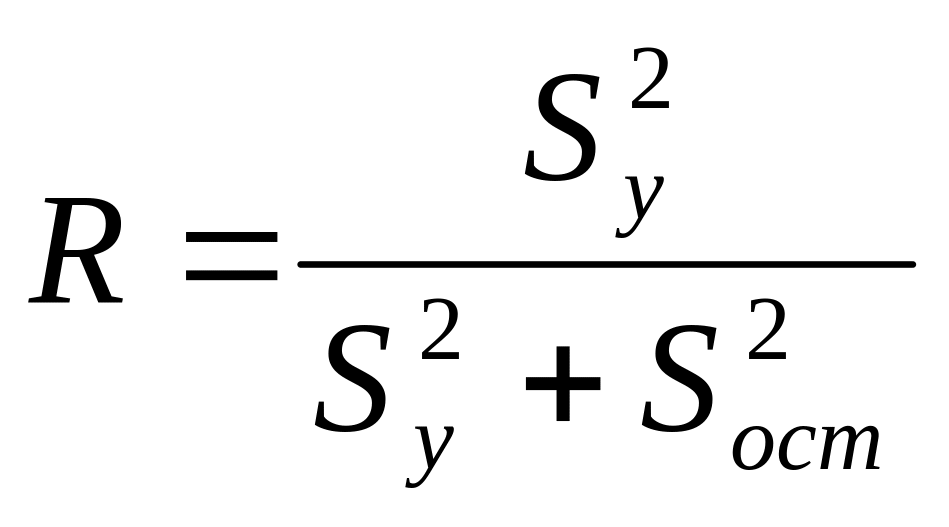 .
(8)
.
(8)
Чем ближе значение R к единице, тем адекватнее уравнение регрессии описывает исследуемый процесс.
