1.4. Ортогональное проецирование.

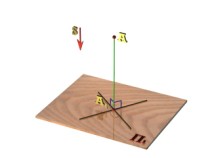
Если направление проецирования перпендикулярно плоскости проекций, параллельное проецирование называется ортогональным (прямоугольным) s  П₁ (AA₁)  П₁. В этом случае проекция А₁, точки А называется ортогональной, или прямоугольной (рис. 1.9). В противном случае проецирование называется косоугольным.

Р ис. 1.9

Ортогональное проецирование, являясь частным случаем параллельного, значительно упрощает построение проекций геометрических фигур и является основным при выполнении комплексных чертежей технических форм (рис. 1.10). Рассмотренные в предыдущих параграфах однопроекционные чертежи геометрических фигур являются необратимыми. 

Pис. 1.10  Рис 1.11

По ним нельзя мысленно воссоздать пространственную форму и размеры изображенного объекта. Существуют различные способы устранения этого недостатка однопроекционных чертежей в зависимости от принятого вида проецирования. Например, при центральном проецировании точку можно проецировать из двух различных центров (рис. 1.12), при параллельном - при помощи двух различных направлений, при ортогональном - на две пересекающиеся плоскости. Нетрудно заметить, что в каждом из этих случаев получаются две проекции А₁, и А'₁, точки А, однозначно определяющие ее положение в пространстве. Следовательно, обратимый чертеж геометрической фигуры должен содержать не менее двух проекций каждой ее точки.

Р ис. 1.12

При построении ортогональных проекций точки на две пересекающиеся плоскости проекций П₁ и П₂ (рис. 1.12) угол между ними принимается равным 90^o. В технике применяются следующие виды обратимых чертежей: 1) комплексные, 2) аксонометрические, 3) перспективные, 4) чертежи с числовыми отметками. В пособии рассматривается первый вид чертежей.

2) Свойства проецирования Основные инвариантные свойства параллельного проецирования.  При параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин), причём степень нарушения зависит как от аппарата проецирования, так и от положения проецируемой геометрической фигуры в пространстве по отношению к плоскости проекции.  Но наряду с этим, между оригиналом и его проекцией существует определённая связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Эти свойства называются инвариантными (проективными) для данного способа проецирования.  В процессе параллельного проецирования (получения проекций геометрической фигуры по её оригиналу) или реконструкции чертежа (воспроизведения оригинала по заданным его проекциям) любую теорему можно составить и доказать, базируясь на инвариантных свойствах параллельного проецирования, которые в начертательной геометрии играют такую же роль, как аксиомы в геометрии.  Для построения обратимого чертежа необходимо иметь две взаимосвязанные проекции оригинала.  Поэтому только прямоугольное (ортогональное) проецирование, по крайней мере, на две взаимно перпендикулярных плоскости проекций является основным методом построения технического чертежа (метод Монжа).  Ортогональное (прямоугольное) проецирование обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием:  1. простоту геометрических построений для определения ортогональных проекций точек  2. возможность при определённых условиях сохранять на проекциях форму и размеры оригинала.  3) Чертеж Монжа

МЕТОД МОНЖА

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала  19 веков, 1789-1818 гг. одним из основателей  знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.

Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometrie descriptive".

Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.

В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П₁   располагают горизонтально, а вторую П₂ - вертикально. П₁ - горизонтальная плоскость проекций, П₂- фронтальная. Плоскости бесконечны и непрозрачны.

Плоскости проекций делят  пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

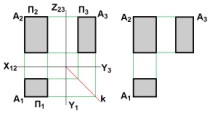
		Линия пересечения плоскостей проекций называется осью координат  и обозначается x12. Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.6).Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называетсяэпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом. Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы). Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций.
Рисунок 6. Пространственная модель двух плоскостей проекций