Вопрос № 6 Гравитационное взаимодействие. Гравитационная и инертная масса. Напряжённость гравитационного поля.

Гравитационное взаимодействие является самым слабым. Однако при наличии больших масс (планеты, звезды и т.д.) оно оказывается весьма существенным.

Сравнивая нормальное ускорение Луны и ускорение свободного падения тел на Земле, Ньютон определил, что чем больше тела, тем сильнее они притягиваются. Но что именно в них «больше»? Назовем эту физическую величину гравитационной массой (m_g), то есть массой, которая определяет гравитацию (тяготение). Закон всемирного тяготения имеет вид где m_gl, m_g2 — гравитационные массы частиц.

Сила тяготения, которая действует на тело со стороны Земли - сила тяжести

, где вектор направлен к центру Земли, M_g — гравитационная масса Земли R – радиус Земли.

Согласно второму закону Ньютона, где — ускорение, которое получает инертная масса т_in под действием силы

Г алилей обнаружил, что для всех тел

Сравнивая это выражение с ,получаем g/a = m_in/m_g. Этой пропорции удовлетворяет, условие: m_in = m_g= m , если

Было проведено много очень точных опытов, которые подтвердили справедливость этого равенства. Его природа пока неясна, так как неизвестна природа гравитационной силы. В дальнейшем мы уже не станем разделять «гравитационную» и «инертную» массы, а будем пользоваться одним понятием «масса».

Английский физик Г. Кавендиш измерял силу притяжения между известными массами, и вычислил гравитационную постоянную: g = 6,67 10-¹¹ м³/(кг с²).

Гравитационные и электромагнитные силы являются фундаментальными — их нельзя свести к другим, более простым, силам. Упругие силы и силы трения не являются фундаментальными, а являются проявление электромагнитного взаимодействия.

Р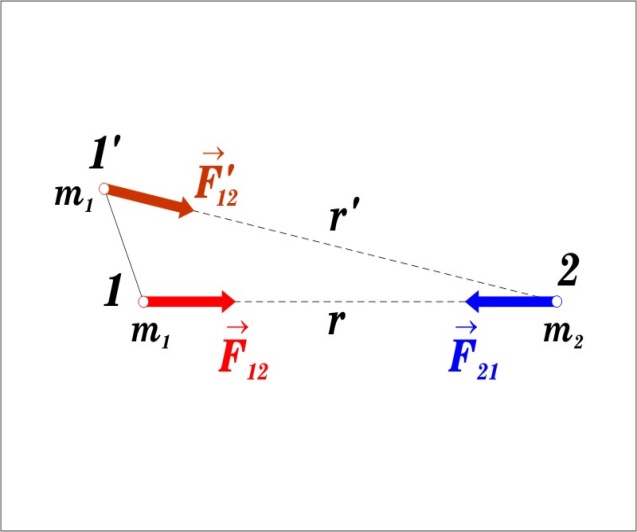 ассмотрим систему из двух электрически нейтральных частиц m₁ и m₂, удаленных друг от друга на расстояние r. (g – гравитационная постоянная).

Взаимодействие частиц осуществляется через гравитационное поле. Первая частица создает в окружающем ее пространстве поле. Поле проявляет себя в том, что на помещенную в какую-либо точку этого поля частицу m₂ действует сила притяжения к первой частице.

Вопрос № 7 Движение относительно неинерциальных систем отсчёта, двигающихся поступательно. Силы инерции.

Законы Ньютона выполняются только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело движется с одинаковым ускорением . Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, поэтому ускорение тела в неинерциальной системе отсчета не будет равно . Ускорение системы

Для поступательно движущейся неинерциальной системы одинаково для всех точек пространства и равно ускорению неинерциальной системы отсчета. Для вращающейся неинерциальной системы в разных точках пространства будет различным.

Пусть результирующая всех сил, обусловленных действием на данное тело со стороны других тел, равна F. Ускорение тела относительно некоторой неинерциальной системы можно в соответствии с представить в виде . Отсюда следует, что даже при F=0 тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением , т. е. так, как если бы на него действовала сила, равная (первый закон Ньютона не выполняется).

П ри описании движения в неинерциальных системах отсчета можно пользоваться уравнениями Ньютона, если вместе с силами, которые обусловлены воздействием тел друг на друга, учитывать силы инерции, которые равны произведению массы тела на взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной системам отсчета:

Уравнение второго закона Ньютона в неинерциальной системе отсчета:

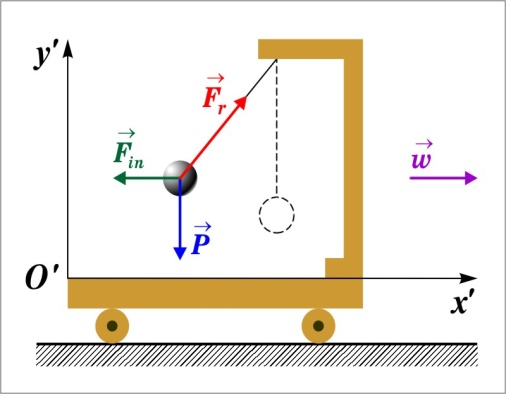
Пока тележка покоится или движется без ускорения, нить расположена вертикально и сила тяжести = . Если тележка движется поступательно с ускорением , нить отклонится от вертикали на такой угол, чтобы результирующая сил и сообщала шарику ускорение, равное . Относительно системы отсчета, связанной с тележкой, шарик покоится, несмотря на то, что результирующая сил и не равна нулю. Это можно формально объяснить тем, на шарик действует еще и сила инерции . Использование сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения.

Силы инерции можно назвать фиктивными силами. Они обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления, а не воздействием на тело со стороны других тел.