46. Магнитный поток.Единица измерения в си.Теорема Остроградского-Гаусса для магнитного поля.

Магнитный поток - Скалярная величина числена = произведению индукции Магнитного поля на величину единичной площадки вектора В.

Фm=Bn*Scos(n;B)

Если вектор В непостоянен во все точках площадках (неоднр. поля) выбираем токую площадку в пределах которой В одинаково тогда

Фm=1Вебер=1Вб=1Тл/м2

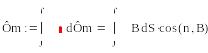
1Максвелн=1Мкс=1*10^8 Вб

Закон пост тока

Т-ма Остр – Гаусса поток вектора магн. индукции через произвольную замкнутую поверхность =0 это есть следствие отсутствия в природе магнитных зарядов

48. Работа по перемещению проводника с I в магнитном поле.

Перемещение элемента dl с током I -du образует с силой dF острый угол. A элемент dl2 с током I 2 -du2 образует с силой dF тупой угол, поэтому работа по перемещение элемента dl берётся со знаком +, а работа dl2 берётся со знаком -.

Работа по перемещению замкнутого контура в магн. поле численно = произвед. силы тока на изменение магнитного потока

49.Работа при перемещении в магнитном поле замкнутого контура с I.

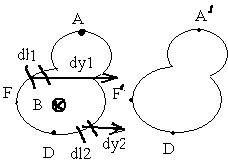
Найдем работу, совершаемую над замкнутым контуром с током при его перемещении в магнитном поле. Вначале предположим, что контур, перемещаясь, остается все время в одной плоскости (рис. 93; вектор В направлен за чертеж). Силы, приложенные к участку контура 1–2, образуют с направлением перемещения острые углы. Следовательно, совершаемая ими работа А₁положительна. Согласно формуле (49.1 dA = idФ) эта работа пропорциональна силе тока в

Рис. 1

контуре i и пересеченному участком 1–2 потоку магнитной индукции. Участок 1–2 пересекает при своем движении поток Ф₀ через заштрихованную поверхность и поток Ф_к, пронизывающий контур в его конечном положении.

Таким образом.

A₁ = i(Ф₀ + Ф_к)

Силы, действующиена участок контура 2–1, образуют с направлением перемещения тупые углы. Поэтому совершаемая ими работа А₂ отрицательна.

Абсолютная величина ее пропорциональна потоку, пересекаемому участком 2–1, который слагается из Ф₀ и Ф_н – потока, пронизывающего контур в начальном положении. Следовательно,

A₂ = i(Ф₀ + Ф_н).

Работа, совершаемая над всем контуром, равна

А=А₁ + А₂ = i(Ф₀ + Ф_к) – i(Ф₀ + Ф_н) = i(Ф_к – Ф_н)

Разность магнитного потока через контур в конце перемещения Ф_к и потока в начале Ф_н дает приращение потока через контур ΔФ. Таким образом,

А = i ΔФ                                                                  (2)

При выводе формулы (2) мы сделали определенные предположения о характере движения контура. Можно показать, что эта формула остается справедливой при любом движении контура в произвольном магнитном поле. В частности, при повороте контура в однородном поле из положения, в котором векторы р_m и В направлены в противоположные стороны, в положение, при котором эти векторы совпадают по направлению, силы поля совершают над контуром работу

A=2iSB

(Ф_н = – BS, вектор В и положительная нормаль имеют противоположные направления, вследствие чего Ф_н отрицателен; Ф_к = BS). Учитывая, что iS = р_m – магнитному моменту контура, получаем

А = 2 p_mВ.

Тот же результат получается с помощью выражения (W = – p_m⋅В) для энергии контура в магнитном поле:

А = W_н – W_к = p_mВ – (–p_mВ) = 2 p_mВ.