16. Порівняння внутрішніх зусиль в тришарнірній арці і еквівалентній балці.

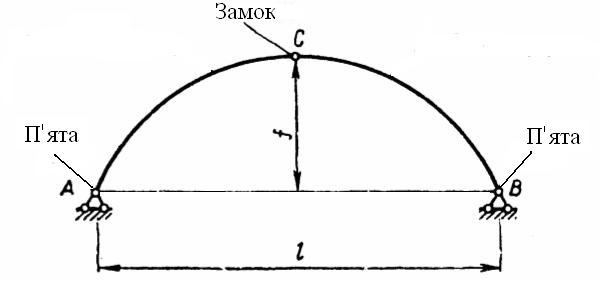Тришарнірна арка – система, яка складається з двох криволінійних стержнів, які поєднуються між собою і основою – шарніром.

В перерізах арки виникає 3 види зусиль M, Q, N.

Зусилля обчислюються як і в рамі Мк= Σ Qк= Σ Nк= Σ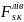

Мк= Σ Qк= Σ Nк= Σ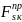

Якщо момент розтягає нижнє волокно – момент додатній.

Якщо поперечна сила оберт. за год. стрілкою – попер. сила додатня.

Якщо повздовжня сила діє від перерізу (розтягуючи) – повздовжня сила додатня.

Для побудови епюр арку розбивають на окремі ділянки, крім того кожна ділянка розбивається ще на окремі ділянки і в кожній точці обчислюємо M, Q, N.

Розрахунок тришарнірної арки на вертикальне переміщення ведеться аналогічно розрахунку деякої балки, з тими ж навантаженнями. Балка називається еквівалентною. Балка без шарніра С.

Згинаючі моменти в арці менші, ніж у балці. Різниця в згинаючих моментах визначається наявністю моменту, створеного розпором.

Поздовжні сили в арці при дії вертикального навантаження завжди стискаючі.

Для побудови епюр арка розбив. на окремі ділянки через характерні точки, кожна ділянка розбив. на пів ділянки на границі кожної ділянки визнач геометричні характеристики У, sinφ, cosφ, потім будуються епюри для еквівалентної балки , .

По формулам визначаються зусилля для арки, отримані зусилля відкладаються від горизонтальної проекції і з’єднуються або прямими або плавними лініями.

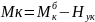; ; N

17 Класифікація плоских рам

Рамою назив. Систему , що складається з прямолінійних стержнів, які поєднуються між собою у вузлах. При розрахунку рам доцільно розподілити їх за якимось ознаками. Для цього зручно скористатись ознаками кінематичного аналізу. Всю сукупність плоских рам можна розділити на прості і складені. До простих можна віднести рами, для яких структурний аналіз здійснюється за один етап, тобто такі, що утворюються з двох або трьох дисківза допомогою звичайних способів з”эднання дисків. Прості в свою чергу діляться на : консольні, балкові,аркові.

До консольних рам можна віднести такі, що є приєднанням двох дисків, одним із яких є диск „земля”, за допомогою припайки.

Балкові рами утворюються з двох дисків за способом Шухова або за способои Полонсо.

Рами. Що утворені за способом шарнірного трикутника можуть відноситись до аркового типу.

До складених рам можна віднести ті, для яких структурний етап кінематичного аналізу здійснюється більше ніж за один етап. Частину складеної рами, що відповідає одному етапу, умовно назив. „поверхом”. Отже кожен поверх може розглядатись як проста рама і тому складену раму можна розглядати як сукупність кількох простиз рам.

18 .Внутрішні зусилля у плоских рамах

Унаслідок діЇ зовнішніх навантажень у перерізах плоских рам виникають згинальні i поздовжні деформацій, а також деформацій зсуву. Цим деформаціям відповідають внутрішні зусилля: згинальні моменти, поздовжні i поперечні сили. Розрахунок рам полягає в обчислені зусиль i в побудові графіків Їхнього розподілу в стержнях. графіки називають епюрами внутрішніх зусиль. Визначення внутрішніх зусиль у стержневих системах було розглянуто в п.п.2.7.2. Нагадаемо ще раз правила Їx обчислення стосовно до рам. Згинальний момент у nepepiзi стержня рами обчислюється як сума моментів ycix сил, що прикладеш до рами по один бiK від перерізу, відносно центра тяжіння перерізу. У рамах знаки згинальних моментів не визначеш. При побудові епюри на стержнях рам ординати прийнято відкладати від розтягнених волокон. Поперечна сила в nepepi3i к-к стержня рами обчислюється як сума проекщй ycix сил, розташованих по один бік від перерізу, на нормаль п до oci стержня в цьому nepepi3i Поперечна сила вважаеться додатною, якщо вона намагаеться повернути відповідну частину стержня стосовно перерізу за годинниковою стршкою. Поздовжня сила в nepepi3i к-к стержня рами обчислюеться як сума проекщй Bcix сил, розташованих по один бік від перерізу, на напрям t oci стержня в цьому nepepi3і Тут також беруть до уваги Bci сили, які діють на одну з частин рами. Поздовжня сила вважаеться додатною, якщо вона розтягуе nepepi3. При обчисленні згинального моменту М^ в даному приклад1 доданки вважаються додатними, якщо моменти вщповщних силових діі викликають розтягування в нижніх волокнах. коли опорні реакціі задовольняють умови рівноваги, внутрішні зусилля, обчислені iз розгляду лівоі чи право! частин рами, матимуть Ti сам1 величини i знаки.

• Якщо на ділянці стержня відсутне будь-яке зовнішне навантаження, то епюра згинальних момеппв змінюеться за лінійним законом, а поперечні i поздовжні сили е постшними. Тому для побудови епюри М достатньо обчислити згинальш моменти в двох перерізах ділянки, а для побудови епюр QiN— величини поперечних i поздовжшх сил в будь-якому одному nepepi3i.

• Я кщо на ділянці стержня розташоване зовнішне розподшене навантаження, то згинальш моменти змінюються за нел1шйним законом (у випадку, якщо навантаження розподілене рівномірно - за законом квадратно! параболи), i тому для побудови епюри М необхщно обчислити згинальні моменти принаймш в трьох перер1зах д1лянки. Епюри Q i N при діі рівномірно розподіленого навантаження змшюються за лішйним законом, i тому необх1дно обчислювати відповідні величини в двох перер1зах. Якщо ж навантаження розподшене нерівномірно, то величини Q i М змінюються за нелінійним законом i для побудови іхніх епюр необхідно обчислювати відповідні величини не менш ніж у трьох перерізах ділянки.