
- •Будівельна механіка як наука
- •2. Класифікація розрахункових схем
- •3. Кінематичний аналіз. Кількісний і якісний етап.
- •4.Кількісний етап кінематичного аналізу
- •5. Якісний аналіз. Способи утворення геометрично незмінюваних систем.
- •7. Аналіз геометричної структури споруди
- •6. Миттєво змінювані системи. Навести приклади.
- •10. Спосіб вирізання вузлів при розрахунку плоских ферм
- •11. Метод наскрізних перерізів для розрахунку плоских ферм
- •12. Окремі випадки рівноваги вузлів ферми
- •13. Розрахунок трьох шарнiрних арок на вертикальне навантаження.
- •14.Розрахунок тришарнірної арки з горизонтальною затяжкою на вертикальне навантаження
- •15. Розрахунок тришарніх арок на навантаження загального вигляду
- •16. Порівняння внутрішніх зусиль в тришарнірній арці і еквівалентній балці.
- •17 Класифікація плоских рам
- •18 .Внутрішні зусилля у плоских рамах
- •19. Перевірка епюр внутрішніх зусиль
- •20. Перевірки розрахунку плоских рам
- •21 . Дійсна і можлива робота зовнішніх зусиль
- •22. Узагальнені сили і узагальнені переміщення. Універсальні позначення переміщень.
- •Продовженя дал
- •23. Формула Максвелла-Мора. Техніка обчислення переміщень.
- •24. Застосування формули Максвелла-Мора для різних розрахункових схем.
- •25. Правило Верещагіна
- •26.Формула Сімпсона–Корноухова
- •27. Обчислення переміщень, зумовлених зміщеннями опор
- •28.Переміщення від дії температури
- •29.Теорема про взаємність робіт (теорема Бетті)
- •30. Теорема про взаємність переміщень
- •31. Теорема про взаємність реакцій
- •32. Теорема про взаємність переміщень і реакцій.
- •33.Матриця податливості і матриця жорсткості
- •34) Oснови розрахунку на рухоме намантаження
- •35.Лінії впливу в статично визначуваних багатопрогонових балках
- •36. Лінії впливу при вузловій передачі навантаження
- •37. Лінії впливу у фермах
- •39. Навантаження нерухомими силовими діями
- •40. Навантаження рухомими силами
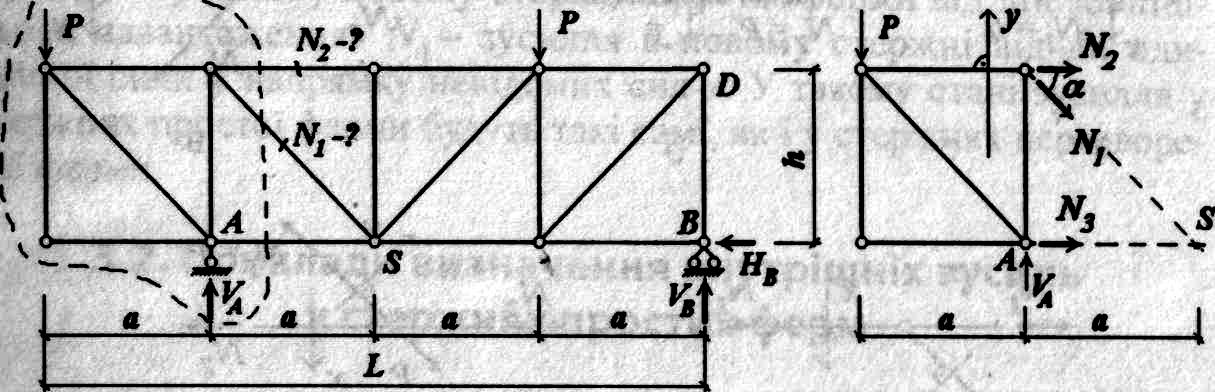
11. Метод наскрізних перерізів для розрахунку плоских ферм
У методі наскрізних перерізів для виділеного фрагмента складаються рівняння моментів відносно моментних точок (точок Ріттера) або рівняння проекцій на координатні осі.
 а
б
а
б
12. Окремі випадки рівноваги вузлів ферми
1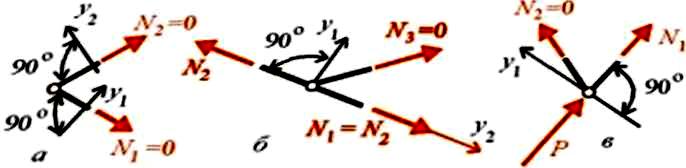 .
У незавантаженому вузлі, в якому
збігаються два стержні,
що не розташовані на одній прямій
(рис. 8.6,а), зусилля в обох стержнях
дорівнюють нулю.
.
У незавантаженому вузлі, в якому
збігаються два стержні,
що не розташовані на одній прямій
(рис. 8.6,а), зусилля в обох стержнях
дорівнюють нулю.
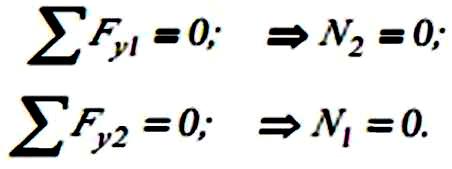 асправді,
рівняння рівноваги у вигляді суми
проекцій на вісі, перпендикулярні до
кожного з двох
стержнів, вміщують лише зусилля в іншому
стержні. Тому маємо
асправді,
рівняння рівноваги у вигляді суми
проекцій на вісі, перпендикулярні до
кожного з двох
стержнів, вміщують лише зусилля в іншому
стержні. Тому маємо
С![]() тержні,
в яких зусилля дорівнюють нулю називаються
нульовими.
тержні,
в яких зусилля дорівнюють нулю називаються
нульовими.
2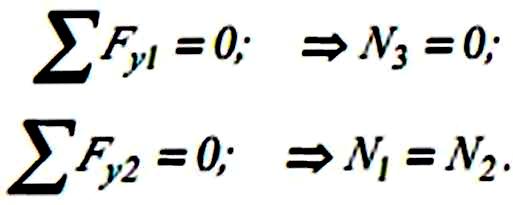 .
У не завантаженому вузлі, в якому
збігаються три стержні, два з яких
розташовані на одній прямій
(рис. 8.6,6), зусилля
В ЦИХ ДВОХ
стержнях дорівнюють одне одному,
а зусилля у третьому стержні
дорівнює нулю, означений стержень є
нульовим. Це випливає із
розв'язання двох рівнянь рівноваги:
.
У не завантаженому вузлі, в якому
збігаються три стержні, два з яких
розташовані на одній прямій
(рис. 8.6,6), зусилля
В ЦИХ ДВОХ
стержнях дорівнюють одне одному,
а зусилля у третьому стержні
дорівнює нулю, означений стержень є
нульовим. Це випливає із
розв'язання двох рівнянь рівноваги:
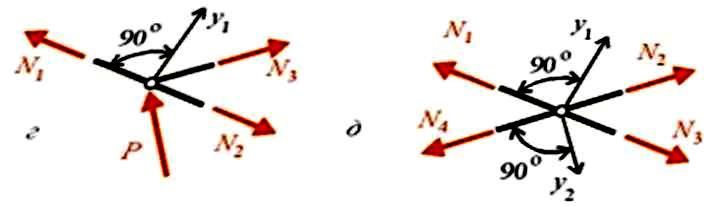
3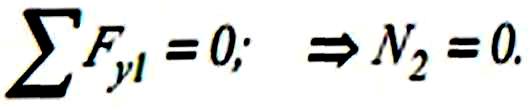 .Якщо
на вузол,в якому збігаються два сержні,
діє зосереджена сила,спрямована вздовж
одного із стержнів (рис 8.6,в), зусилля в
другому стержні дорівнює нулю. Отже,
цей стержень є нульовим. Справді,складаючи
рівняння рівноваги у вигляді суми
проекцій на вісь, перепендик. до сили,
маємо:
.Якщо
на вузол,в якому збігаються два сержні,
діє зосереджена сила,спрямована вздовж
одного із стержнів (рис 8.6,в), зусилля в
другому стержні дорівнює нулю. Отже,
цей стержень є нульовим. Справді,складаючи
рівняння рівноваги у вигляді суми
проекцій на вісь, перепендик. до сили,
маємо:
4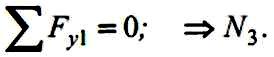 .
У завантаженому вузлі, в якому збігаються
три стержні, два з яких розташовані на
одній прямій (рис.8.6,г), зусилля в третьому
стержні можна визначити з рівняння
рівноваги у вигляді суми проекцій на
вісь, перпендикулярну до цих двох
стержнів:
.
У завантаженому вузлі, в якому збігаються
три стержні, два з яких розташовані на
одній прямій (рис.8.6,г), зусилля в третьому
стержні можна визначити з рівняння
рівноваги у вигляді суми проекцій на
вісь, перпендикулярну до цих двох
стержнів:
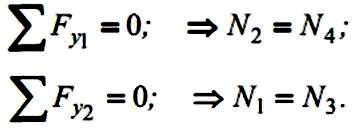
13. Розрахунок трьох шарнiрних арок на вертикальне навантаження.
Плоска
геометрично незмiнювана
стержнева система утворена поэднанням
двох криволiнiйних
дискiв
i
диску земля за допомогою трьох шарнiрiв
що не лежать на однiй
прямiй
називаэться
тришарнiрною
аркою
. Опорнi
шарнiри
називаються пятами
а шарнiр
мiж
дисками арками замком.
Вiдстань
мiж
пятами арки –
прогон,
а вертикальний габаритний розмiр-
стрiла
пiдйому
арки.
Вiсь
арки описуэться функц. y
= ƒ(X), яка задаэться рiвнянням.
Для розрахунку арки потрiбно
знати координати точок осi
Хi
та Yi
а й кути нахилу дотичноii
до осi
арки щодо координатноii
осi
Х. Найбiльш
вживаними функцiями
осi
арки э: Парабола: y
=  x(l-x),
tan
x(l-x),
tan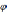
 =
=

 Синусоiiда:
y
=ƒsin
Синусоiiда:
y
=ƒsin
 ;
Коло:
y
=
;
Коло:
y
=  Особливiстю
арочних розрахункових схем э те що при
дii
вертикального навантаження в пятах
крiм
вертикальних виникають й горизониальнi
складовi
реакцii-
розпiр.
Для сприйняття розпору влаштовують
затяжку.
При
вертикальному навантаженi
на арку без затяжки внутрiшнi
зусилля в ii
перерiзах
можна визначити за формулами:
Особливiстю
арочних розрахункових схем э те що при
дii
вертикального навантаження в пятах
крiм
вертикальних виникають й горизониальнi
складовi
реакцii-
розпiр.
Для сприйняття розпору влаштовують
затяжку.
При
вертикальному навантаженi
на арку без затяжки внутрiшнi
зусилля в ii
перерiзах
можна визначити за формулами:
 =
= -
-

 ;
;

 =
= -
-

 ;
;

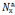 =
- (
=
- ( ;
;

 ;
;
 -
функц.внутрiшнiх
зусиль у поперечних перерiзах
арки вiд
координати Х;
-
функц.внутрiшнiх
зусиль у поперечних перерiзах
арки вiд
координати Х;

 -функц.
внутр. зусиль у поперечних перерiзах
еквiвалентноii
балки.
-функц.
внутр. зусиль у поперечних перерiзах
еквiвалентноii
балки.
 ;
;
 функцii
що описують геометрiю
осi
арки; Н – розпiр
арки.Для арки iз
простою горизонтальною затяжкою на
висотi
a
:
функцii
що описують геометрiю
осi
арки; Н – розпiр
арки.Для арки iз
простою горизонтальною затяжкою на
висотi
a
: 
 =
;
=
;
=
;
=
;

 =
=
 ;
над
затяжкою:
=
-Н(
;
над
затяжкою:
=
-Н(
 ;
=
-
;
=
- (
;
Розпiр
арки визначаэться : з затяжкою- Н=
;
=
-
;
=
- (
;
Розпiр
арки визначаэться : з затяжкою- Н= без затяжки Н=
без затяжки Н=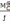 ;
; 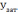
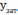 – визн. Так само як «у» для синусоiди
, параболи…
– визн. Так само як «у» для синусоiди
, параболи…

