25. Правило Верещагіна

За правилом Верещагіна для обчислення інтеграла \MjMpdx достатньо помножити площу

епюри I на ординату епюри, що береться під центром тяжіння епюри (рис.3.8):

Я кщо ордината y_t i площа А розташовані по один і той самий бік стержня, добуток береться зі знаком "плюс". Насправді, розглянемо обчислення інтеграла

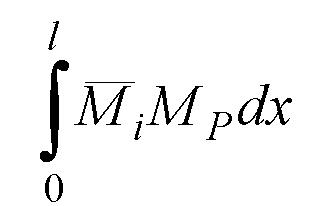на прикладі перемножения двох

епюр (рис.3.9), одна з яких мае довільний характер, а друга -обмежена прямою. Добуток є елементарною площею, яка береться на епюрі

О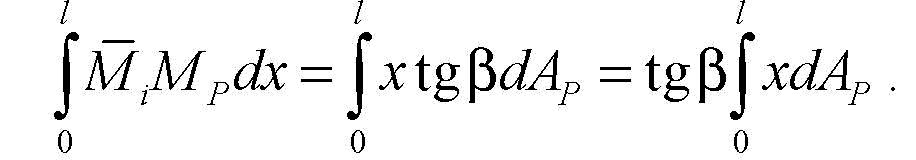 рдинату на прямолінійній епюрі можна представити у вигляді М_і = xtg(3 . Зрештою інтеграл набуває вигляду:

Інтеграл у правій частині співвідношення - це статичний момент Sp площі епюри стосовно осі у\, яка проходить через точку перетину епюри з прямою, що збігається з віссю стержня. Як відомо, статичний момент площі дорівнює добутку площі на координату центра її тяжіння . На цій під ставі маємо

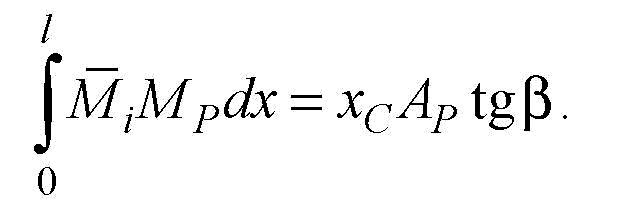
Необхідно звернути увагу:

• принаймні одна з епюр , які перемножуються, має бути прямолінійною;

• ордината у_і повинна бути взята на прямолінійній епюрі.

I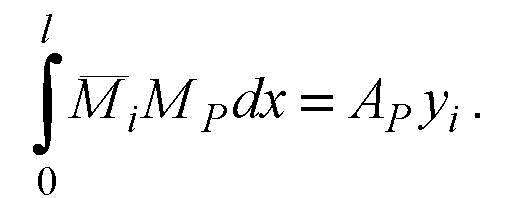 нарешті, помітивши, що остаточно одержуємо:

26.Формула Сімпсона–Корноухова

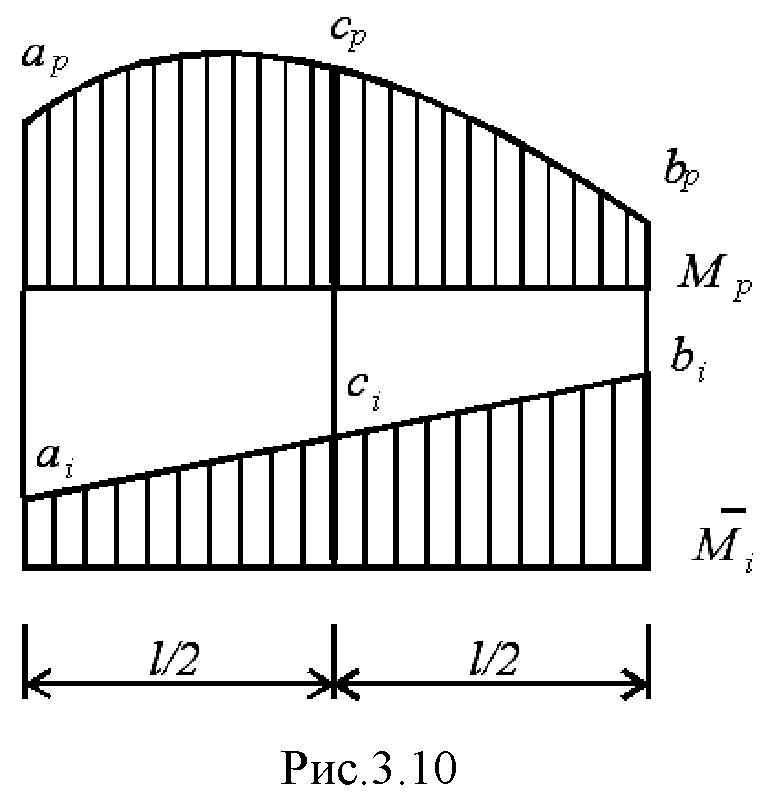– це окремий випадок відомої з математичного аналізу формули Сімпсона (формули парабол) для обчислення визначених інтегралів, коли інтервал інтегрування розкладається на дві ділянки (рис.3.10):

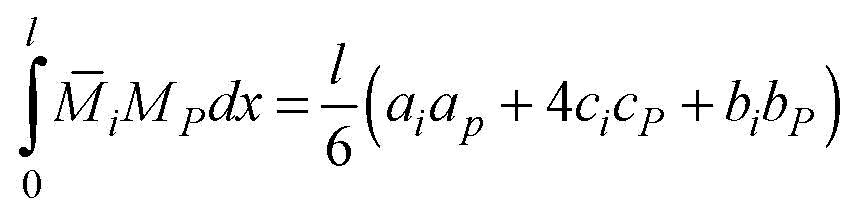
При використанні формули Сімпсона–Корноухова необхідно, щоб обидві перемножувані епюри не мали зламів, розривів та точок перегину. В противному разі інтервал інтегрування треба розкласти на окремі підінтервали.

Приклад 3.1. Обчислити кут повороту в перерізі k рами (рис.3.11,а).

П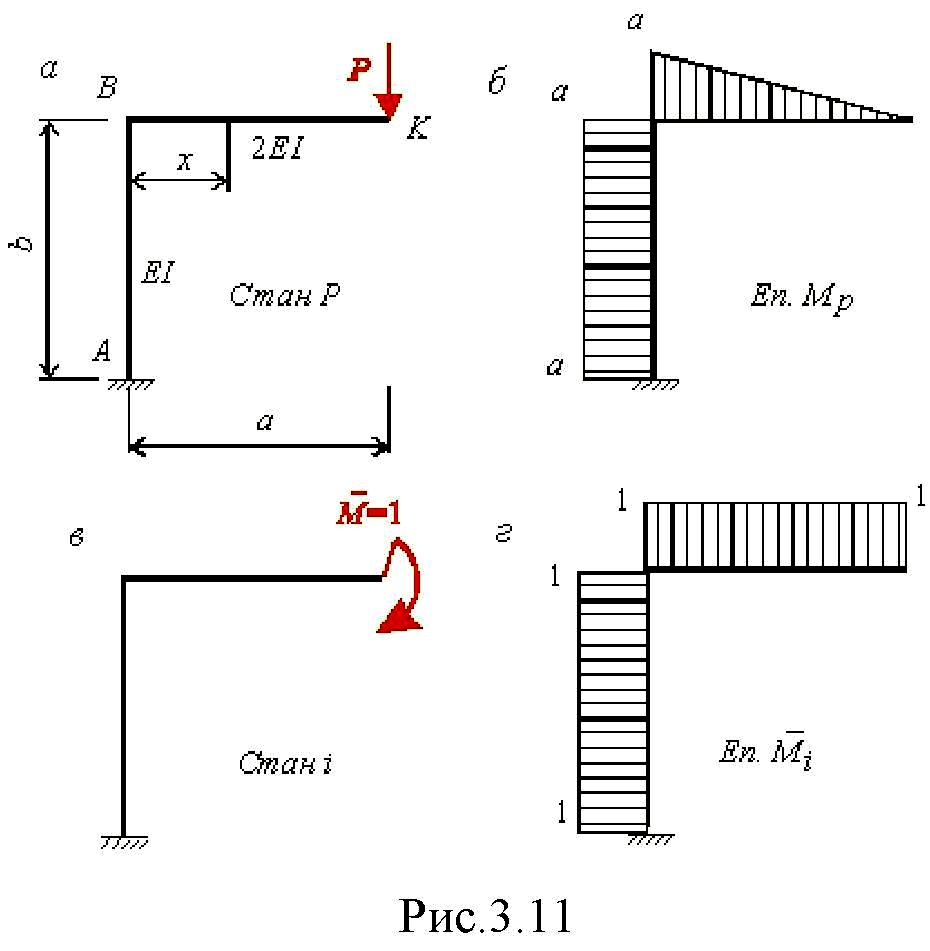 роцес розв’язання містить чотири етапи:

1. Визначення зусилля від зовнішнього навантаження. На ригелі: M _p = P( a - x ), на стійці

M_p = Pa. Епюру M_p побудовано на рис.3.11,б.

2. Створення допоміжного стану. Допоміжний стан (стан i) зображено на рис.3.11,в.

3. Визначення зусиль в допоміжному стану: на ригелі M_i =1, на стояку M_i =1. Епюру M_i

побудовано на рис.3.11,г.

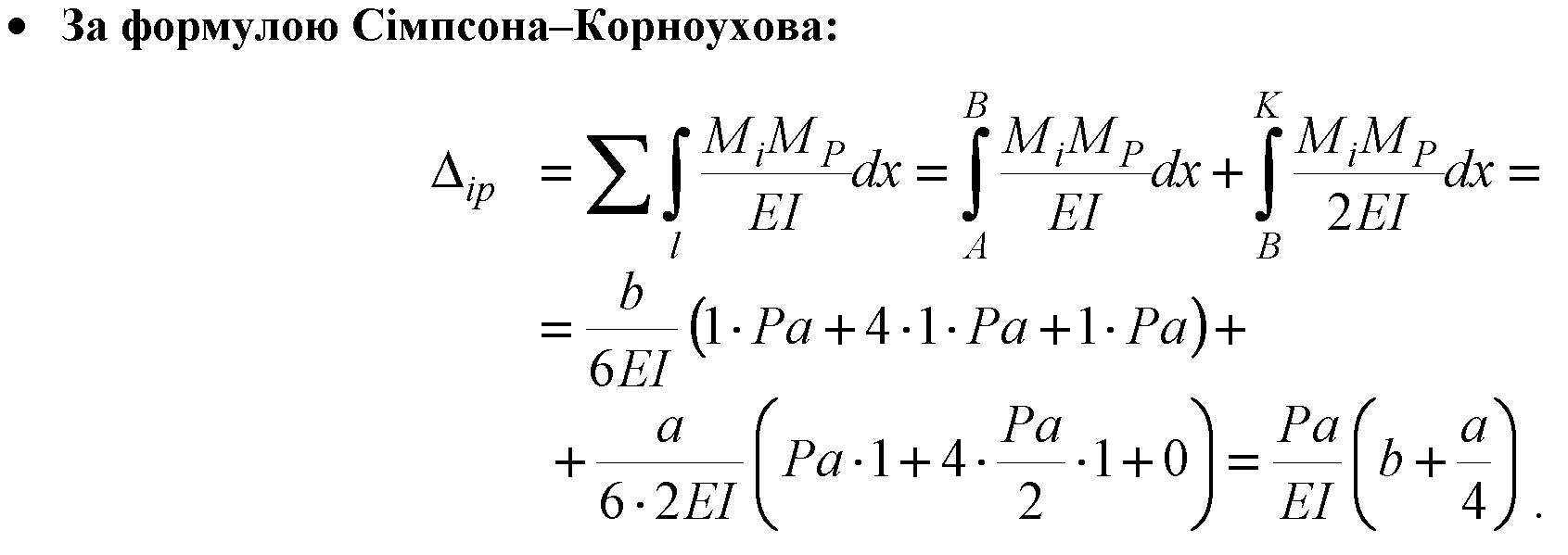4. Обчислення переміщення за формулою Мора.

27. Обчислення переміщень, зумовлених зміщеннями опор

Якщо опори споруди зміщуються, то споруда змінює своє розташування, а її точки одержують переміщення. При цьому неважко впевнитись у тому, що в статично визначува­них системах опорні реакції, внутрішні зусилля і деформації елементів дорівнюють нулю.

Для обчислення якогось переміщення, зумовленого зміщенням опор споруди, скорис­таємось принципом можливих переміщень. Розглянемо два можливі стани споруди.

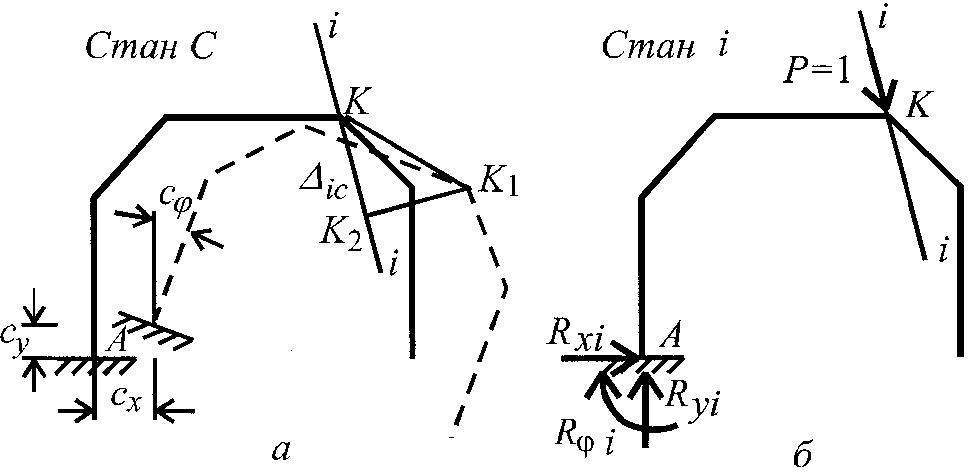
Перший стан С зумовлено поступальними переміщеннями затиснення Cx і Cy в напрямі координатних осей і поворотом на кут Cф. Як уже згадувалось, деформа­ції елементів у цьому стані не виникають. У допоміжному стані і на раму в напрямі і-і діє одинична зосереджена сила, яка спричинює опорні реакції Rxi, Ryi і Rфi . Розглянемо роботу сил стану і на переміщеннях стану С. Згідно з принципом можливих переміщень.

А_іс+и_іс=0. (3.36)