Абсолютные показатели вариации включают:

• размах вариации

• среднее линейное отклонение

• дисперсию

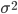
• среднее квадратическое отклонение

Размах вариации (r)

Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Среднее линейное и квадратическое отклонение

Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

19. Ряды динамики. Классификация.

Ряды динамики – статистические данные , отображающие развитие во времени изучаемого явления . Их также называют динамическими рядами , временными рядами .

В каждом ряду динамики имеется два основных элемента :

1) показатель времени t ;

2) соответствующие им уровни развития изучаемого явления y;

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы , кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления . Они могут выражаться абсолютными , относительными или средними величинами .

Ряды динамики различаются по следующим признакам :

1) По времени . В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам . В соответствии с этим ряды динамики подразделяются на моментные и интервальные .

2) По форме представления уровней . Могут быть построены также ряды динамики , уровни которых представляют собой относительные и средние величины . Они также могут быть либо моментными либо интервальными .

В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла , так как относительные и средние величины являются производными и исчисляются через деление других величин .

3) По расстоянию между датами или интервалам времени выделяют полные или неполные ряды динамики .

Полные ряды динамики имеют место тогда , когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами . Это равноотстоящие ряды динамики . Неполные – когда принцип равных интервалов не соблюдается .

4) По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики . Если ведется анализ во времени одного показателя , имеем изолированный ряд динамики . Комплексный ряд динамики получается в том случае , когда в хронологической последовательности дается система показателей , связанных между собой единством процесса или явления .

20. Правила построения динамических рядов.

Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности чи-словых значений статистического показателя, характеризующих изменение общественных явлений во времени.

В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у.

Уровни ряда -- это показатели, числовые значения которых составляют динамический ряд. Время -- это моменты или перио-ды, к которым относятся уровни.

Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно дли-тельной динамике. На основную закономерность динамики на-кладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уров-ней, именуемой трендом, является одной из главных задач ана-лиза рядов динамики.

По времени, отраженному в динамических рядах, они разде-ляются на моментные и интервальные.

Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные да-ты (моменты времени).

Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц).

Уровни в динамическом ряду, могут быть представлены абсолютными, средними или относительными величинами.

По расстоянию между уровнями ряды динамики подразде-ляются на ряды с равностоящими и неравностоящими уровнями по времени

При построении динамических рядов необходимо соблюдать определенные правила: основным условием для получения пра-вильных выводов при анализе рядов динамики и прогнозирова-нии его уровней является сопоставимость уровней динамиче-ского ряда между собой.

Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам изме-рения, времени регистрации, ценам, методологии расчета и др.

Сопоставимость по территории предполагает одни и те же границы территории.

Сопоставимость по кругу охватываемых объектов означа-ет сравнение совокупностей с равным числом элементов.

При этом нужно иметь в виду, что сопоставляемые показате-ли динамического ряда должны быть однородны по экономиче-скому содержанию и границам объекта, который они характеризуют (однородность может быть обеспечена одинаковой полно-той охвата разных частей явления).

Сопоставимость по времени регистрации для интервальных рядов обеспечивается равенством периодов времени, за которые приводятся данные.

Сопоставимость по ценам. При проведении к сопостави-мому виду продукции, измеренной в стоимостных (ценностных) показателях, трудность заключается в том, что, во-первых, с те-чением времени происходит непрерывное изменение цен, а во-вторых, существует несколько видов цен.

Сопоставимость по методологии расчета. При определе-нии уровней динамического ряда необходимо использовать еди-ную методологию их расчета.

21. Показатели анализа рядов динамики.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относят:

1)      абсолютный прирост;

2)      темпы роста;

3)      темпы прироста;

4)      абсолютное значение одного процента прироста.

В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.