1.8. Періодичний нестаціонарний процес теплопровідності

Для процесів такого типу замість початкових умов повинна ставитися умова періодичності

, (4.59)

де – період процесу. Для характеристики періодичних процесів використовують також частоту і кругову частоту.

Розглянемо задачу теплопровідності напівобмеженого масиву, температура поверхні якого змінюється по періодичному закону (рис. 4.13). В даному випадку зручніше користуватися надлишковою температурою , оскільки така заміна призводить до нульової граничної умови на нескінченності.

Математичний опис включає диференціальне рівняння теплопровідності в одновимірній постановці

(4.60)

і крайові умови

. (4.61)

Для побудови розв’язка скористаємося достатньо очевидними фізичними міркуваннями:

1. Температура для кожного фіксованого періодично змінюватиметься в часі.

2. Вглиб масиву розповсюджуються теплові хвилі, тому розв’язки повинні містити множник, що описує поведінку прогресуючої хвилі виду . Тут – хвильове число, що характеризує кількість хвиль завдовжки , що укладається на відрізку завдовжки .

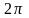3. Оскільки ми припустили, що 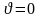в глибині масиву, температурні коливання повинні затухати по мірі віддалення від поверхні. Можна припустити, що затухання описується експоненціальним законом вигляду , де m носить назву декремента затухання.

Таким чином, передбачуваний розв’язок приймає наступний вигляд:

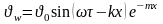(4.62)

Н

Рис. 4.13. Зміна температури поверхні при періодичному процесі нестаціонарної теплопровідності.

еважко переконатися, що рівняння (4.62) задовольняє як граничним умовам, так і умовам періодичності. Якщо ж воно при певних значеннях К і m задовольняє диференціальне рівняння теплопровідності (4.60), то в цьому випадку воно є розв’язком поставленої задачі. Продиференціюємо (4.62) окремо за часом і двічі по координаті:

,

.

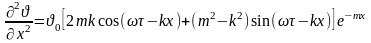Для того, щоб виконувалося рівняння (1.60), необхідне дотримання двох умов:

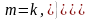. (4.63)

З останньої рівності виходить, що 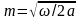і остаточний розв’язок задачі приймає наступний вигляд:

. (4.64)

Графічна інтерпретація розв’язку представлена на рис 4.13.

Аналіз розв’язку. Довжина теплової хвилі складає

. (4.65)

На глибині амплітуда коливань температури зменшується в , тобто в 535 разів. Таким чином, значення є глибиною проникнення температурних флуктуацій. Як випливає з (4.65), вона сильно залежить від періоду протікання процесу і матеріалу масиву. Так, для ґрунтового покриву Землі добові коливання температури проникають на глибину м, а річні – до 20 м.

Встановимо тепер, як поводиться тепловий потік на поверхні тіла:

,

, (4.66)

або

. (4.66а)

Рис. 4.14. Залежності температури і теплового потоку від відстані від поверхні і часу при синусоїдальному законі зміни температури поверхні.

Виявляється, що тепловий потік на поверхні зсунутий по фазі відносно зміни температури. Так само можна показати, що і для всієї решти точок тіла тепловий потік випереджає по фазі коливання температури на (рис. 4.14). В середньому за період потік тепла .

Амплітуда коливань теплового потоку

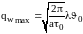. (4.67)