
- •Система двух линейных уравнений с двумя неизвестными. Совместные и несовместные системы.
- •Вывод формулы Крамера решения системы второго порядка.
- •4.Исследование системы 2-ого порядка с помощью определителей. Геометрическая интерпретация.
- •5. Минор, дополнительный к выделенному элементу матрицы. Алгебраическое дополнение к выделенному элементу матрицы.
- •6. Вычисление определителя 3-го порядка разложением по элементам строки или столбца.
- •7. Решение системы линейных уравнений 3-го порядка. Условие
- •Решение системы линейных алгебраических уравнений методом Крамера
- •10. Однородные системы. Условие существования нейтральных решений и их нахождение.
6. Вычисление определителя 3-го порядка разложением по элементам строки или столбца.
Определитель 3-го порядка, вычисляется 2 способами:
А) Правило треугольника
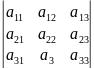 =
=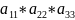 +
+
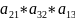 +
+
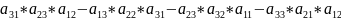
Перемножаемые элементы не должны стоять в одной строке и столбце
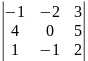 =
-1*0*2+4*(-1)*3+1*5*(-2)-3*0*1-5*(-1)*(-1)-2*(-2)*4=-12-10-5+16=-11
=
-1*0*2+4*(-1)*3+1*5*(-2)-3*0*1-5*(-1)*(-1)-2*(-2)*4=-12-10-5+16=-11
Б) Теорема Лапласа (разложение определителя по строке и столбцу)
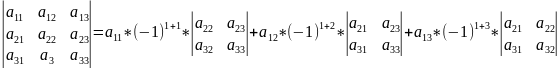
=
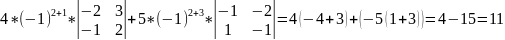
Применяется для решения 3-х линейных уравнений с 3-мя неизвестными по формуле Крамера (метод определителей)
7. Решение системы линейных уравнений 3-го порядка. Условие
|
|
Решение системы линейных алгебраических уравнений методом Крамера
Систему уравнений можно представить в матричной форме: Ax = B, где А - основная матрица (квадратная матрица), В - матрица свободных членов.
Теперь необходимо найти 4 определителя: определитель основной матрицы (определитель системы) и 3 определителя дополнительных матриц. Перед нахождением определителей советуем ознакомиться с теорией определителей матриц, а для нахождения определителей советуем использовать нашу программу - нахождение определителя матрицы.
Перепишем систему линейных алгебраических уравнений в матричную форму. Слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
-

2
1
2
3
-1
2
4
-1
5
1
1
-3
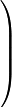
Найдем определитель основной матрицы:
Δ = |
|
= |
- 2 · 1 · 5 + 1 · 2 · 4 - 2 · 3 · 1 + 2 · 1 · 4 + 2 · 1 · 2 - 5 · 1 · 3 = -11 |
|
Определитель основной матрицы не равен нуля, значит система невырожденная.
Найдем определители 3 дополнительных матриц:
Дополнительная матрица получается из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов.
Δ 1 = |
|
= |
- 1 · 1 · 5 - 1 · 2 · 3 - 2 · 1 · 1 - 2 · 1 · 3 + 2 · 1 · 1 - 5 · 1 · 1 = -22 |
|
Δ 2 = |
|
= |
2 · 1 · 5 + 1 · 2 · 4 - 2 · 3 · 3 - 2 · 1 · 4 + 2 · 3 · 2 - 5 · 1 · 3 = -11 |
|
Δ 3 = |
|
= |
2 · 1 · 3 + 1 · 1 · 4 - 1 · 3 · 1 + 1 · 1 · 4 + 1 · 1 · 2 + 3 · 1 · 3 = 22 |
|
Найдем решения системы алгебраических уравнений:
х1 =Δ1/Δ=2 х2 =Δ2/Δ=1 х3 = Δ3/Δ = -2
