Этапы формирования у школьников познавательных средств, связанных с понятием "теорема".

Пропедевтический этап, который осуществляется в V-VI классах. Он описан довольно широко в методической литературе, в частности, Г. И. Саранцевым [37]. Цель этой пропедевтики состоит в том, чтобы с помощью специально подобранных упражнений, заданий учитель формировал у школьников

• потребность в обосновании утверждений;

• начала дедуктивного мышления;

• понимание структуры наиболее часто употребляемых умозаключений (силлогизмов, правил выводах)

• умения, связанные с методами обоснования или опровержения рас­суждений (наиболее благоприятной в этом отношении нам представляется тема, связанная с делимостью чисел).

Второй этап связан непосредственно с введением терминов "теорема, "доказательство теоремы". Явно эти понятия вводятся обычно в курсе геометрии VII класса, чаще всего это делается авторами попутно, как бы между строк, без должных разъяснений. Например, в учебни­ке [10] понятие "теорема" вводится в теме "Первый признак равенства треугольников", и сразу же идет довольно сложное для понимания школьниками его доказательство.

Таблица 6

Диагностируемые учебные цели при изучении теорем

Категория учебных целей	Критерии достижения целей
	Цель считается достигнутой, если ученик:
1.Знание	формулирует теорему; -вставляет пропущенные слова в формулировке; -воспроизводит доказательство ; -вставляет пропуски в доказательство;
2.Понимание	-создает модель (графическую, символическую) к теореме, выделяет в соответствии с ней условие и заключение; -проводит доказательство при новой конфигурации и в новых обозначениях; -описывает основную идею (прием, способ, метод) доказательства; -указывает теоремы, которые доказывались этим же приемом; -составляет план доказательства; -выделяет базис доказательства; -указывает, для решения каких задач можно использовать данную теорему; -описывает способы рассуждения на этапах открытия закономерности, поиска доказательства
Применение (в стандартных	-применяет теорему в новых стандартных ситуациях; -составляет дидактические задачи на применение теоремы; -применяет метод, прием доказательства в решении задач и в доказательстве других теорем

Традиционная трудность в усвоении этого материала школьниками объясняется прежде всего тем, что новым в изучаемом содержании является как информационный компонент (первый признак равенства треугольников и его непростое доказательство), так и новые методологические знания, связанные с понятием теоремы, сущностью доказательства, построением правил вывода. В этой связи представляется целесообразным познакомить школьников с понятием теоремы и ее доказательством заранее, на простом примере (свойство смежных или вертикальных углов), посвятив этому отдельный урок.

Учитывая, что доказательство первого признака равенства треугольников само по себе довольно сложно и то, что школьники пока еще не владеют, познавательными средствами, его изучение целесообразно проводить или традиционным объяснительно-иллюстративным мето­дом, или методом проблемного изложения, не вовлекая пока учащихся в самостоятельный поиск. Важно, чтобы учащиеся прослушали образцы рассуждений учителя, в частности образец проведения доказательства. При этом целесообразно правильно строить силлогизмы: большая посылка, малая посылка → вывод, но не наоборот. В учебниках по методике часто рекомендуется записывать доказательство в два столбца:

I П

Утверждение Обоснование

Такая запись будет уместна, когда школьники осознают суть доказа­тельства на последующих этапах обучения.

Практика показывает, что требует целенаправленной работы на пер­вых порах и обучение приему, "применение теорем". Действительно, изучив тему "Равенство треугольников", значительная часть школьников в контрольной работе, решая задачу на доказательство равенства тре­угольников, пишет: "Наложим треугольник на треугольник...", т. е. использует прием доказательства теоремы, но не саму теорему. Поэтому нужна система упражнений, обучающая приему "применение теоремы".

Приведем один из возможных вариантов такой системы на примене­ние первого признака равенства треугольников. На доске изображена серия рисунков:

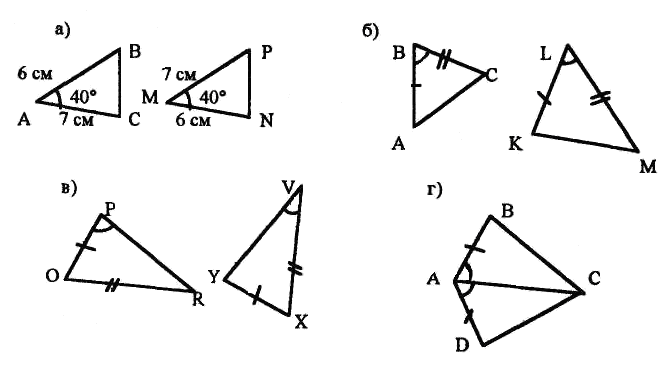
Задания учителя:

• Как доказать, что треугольники ABC и MNP на рис. ба равны? Возможны два варианта ответов: наложение и применение теоремы. Учитель разъясняет преимущество и смысл второго способа.

• Равны ли треугольники, изображенные на рис. 6а; на рис. 6в?

• Как изменить данные на рис. 6в, чтобы возможно было применить теорему о первом признаке равенства треугольников?

Для слабых учеников, возможно, следует заготовить специальные карточки, в которых отражен соответствующий алгоритм применения теоремы.

Третий этап овладения школьниками методологическими знания ми, связанными с такой дидактической единицей, как теорема, продол жается в течение всего периода занятий математикой и является, как уже было сказано, долговременным. Технология работы с теоремой может быть представлена схемой (табл. 7). В работе Г. И. Саранцева, на которую мы неоднократно ссылаемся, показана роль упражнений в реализации каждого этапа. Мы же остановимся более детально на этапах "восприятие", "осознание, осмысление" и опишем, как можно организовать деятельность школьников с тем, чтобы они усваивали не только информационный компонент, но и овладевали познавательными средствами. Как отмечалось в первой главе, это возможно лишь в том случае, если учитель организует учебно-познавательную деятельность школьника адекватно тому, как шел процесс познания в математике. Следовательно, при изучении теорем школьники должны включаться в деятель­ность по "открытию" закономерности, отражаемой в изучаемой теореме, выдвижению гипотез, в поиск доказательства их истинности или опровержения, а также осознавать способы, методы и приемы, с помощью которых реализуется эта деятельность.

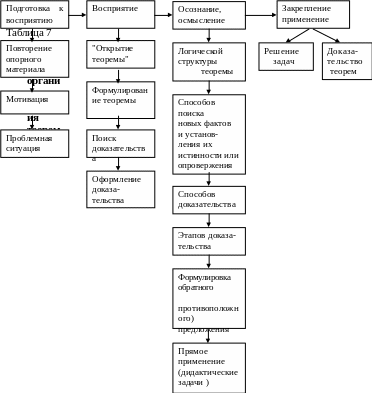
К числу эвристических методов науки прежде всего относятся на­блюдение и сравнение, эксперимент и обобщение, неполная индукция, аналогия, интуиция. Все эти методы позволяют выдвинуть гипотезы, которые требуют установления их истинности или ложности. В то же время к открытию математических фактов приводят и дедуктивные рассуждения(п. 1. 2).Проиллюстрируем сказанное на примерах.

Неполная индукция- это умозаключение, которое делается на основе рассмотрения некоторых частных случаев, причем число этих случаев не охватывает всего, их множества. Естественно, что полученное таким образом умозаключение может быть только гипотезой. В курсе математики деятельность учащихся по выдвижению гипотез на основе неполной индукции организуется через моделирование, измерение, вычисление, построение и анализ хорошо выполненных рисунков. Так, теорему Виета учащиеся могут "открыть" путем правильно направленных учителем вычислений; измерением целесообразно воспользоваться в теме "Признаки равенства треугольников", чтобы помочь учащимся сформулировать соответствующую гипотезу; моделированием можно установить, что сумма углов треугольника равна 180°, то, что биссектрисы углов треугольника пересекаются в одной точке, ребята могут увидеть на чертеже.

Для развития гибкости и критичности мышления важно уже на этом этапе варьировать ситуации, проводить их сравнение. Например, после того как учащиеся на основе построения, измерения или моделирования (перегибания) "откроют" свойство высоты равнобедренного треугольника, проведенной из его вершины, целесообразно сразу же построить высоту к боковой стороне и показать, что она найденным для первой высоты свойством не обладает. И лишь после этого формулировать соответствующую теорему в форме гипотезы.

Аналогия — в переводе с греческого означает "соответствие", "сходство". Умозаключение по аналогии переносит знание, полученное из рассмотрения одних объектов, на другие объекты, менее изученные, но сходные с первыми по некоторым свойствам. Аналогия на протяжении многих тысячелетий являлась основным методом научного исследования. Аналогия при изучении теорем может помочь школьникам как "открыть" теорему, так и найти способ доказательства, а возможно, и то и другое.

Пример.

Приведем фрагмент урока, посвященного изучению площади трапе­ции. Учитель начинает с повторения опорного материала.

• Что такое площадь многоугольника (какими свойствами она обла­дает)?

• Площадь какого многоугольника мы можем находить, исходя из этого?

• Площадь какого многоугольника мы нашли на основании общих свойств площади?

• Какой прием мы использовали для вывода площади прямоугольника? (достраивание до фигуры, площадь которой известна, — до квадрата — и разбиение ее на квадраты и прямоугольники).

Аналогичные вопросы задаются при повторении площади паралле­лограмма и треугольника. В процессе такой беседы на доске появляется постепенно следующая запись (рис. 7):

площадь многоугольника — положительное число свойства: 1...,2..., З....

ПЛОЩАДЬ

S

S = a² S = ab S = ah S(a,b,h)-?

Рис. 7

Подводится итог:

1. Площадь каждой изученной фигуры выражается через сторону и высоту к ней.

2 Для вывода, всех формул применяется один и тот же прием (указан выше)

Какой четырехугольник изучали на прошлых уроках еще?

На рисунке появляется последняя фигура — трапеция.

• Проводя аналогию с тем, что нам уже известно, как вы думаете, через какие элементы можно выразить площадь трапеции? (После обсуждения останавливаются на гипотезе, что, наверное, через основания а, b и высоту h).

• 

  •Попытайтесь найти эту закономерность, используя прием "достраивания" и "разбиения". У кого какие варианты, как можно про­водить дополнительные построения, чтобы к нахождению площади трапеции можно было подойти через площади известных многоугольников? Учащиеся начали предлагать свои варианты (рис. 8).

Всего было предложено семь рисунков. После появления на доске первых трех, класс замер в ожидании новых предложений, и каждый следующий случай сопровождался одобрительным гулом и улыбками.

Далее учитель каждому ряду дал задание: найти площадь трапеции, зная a,b и h по рисункам а), г), д) соответственно. В результате в классе доказали теорему тремя способами. Желающим было предложено дома найти свои способы доказательства.

Включение школьников в поисковую деятельность на основе неполной индукции и аналогии позволяет формировать у них не только логическое мышление, но и интуитивное, которое является необходимым компонентом творческого мышления независимо от их будущей профессиональной деятельности.

Дедуктивные умозаключения. К открытию новых закономерностей, доказательств могут привести и дедуктивные умозаключения. В этом случае доказательство идет впереди формулировки теоремы.

Пример. Опишем еще один урок, который был проведен нами при изучении теоремы о свойстве отрезков пересекающихся хорд окружности.

Цель урока состояла в том, чтобы показать учащимся, как они должны рассуждать, чтобы прийти к самостоятельному получению новых фактов.

Учитель начинает урок со следующего вступления.

Мы с вами доказываем уже сформулированные теоремы, кем-то открытые. Но как люди приходят к открытию новых фактов? На сегодняшнем уроке мы попытаемся получить новые теоремы сами, используя различные приемы рассуждений.

Постройте окружность ω(О, R) точку М внутри полученного круга проведите через точку М две пересекающиеся хорды АВ и СD (рис. 9).

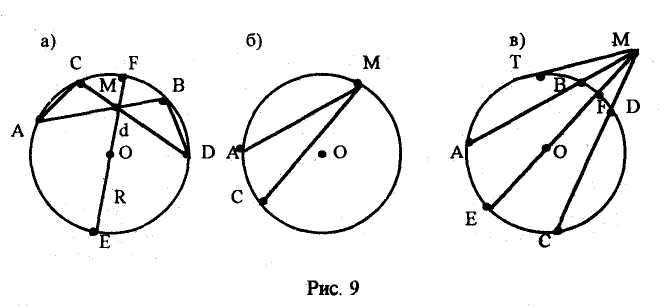
Получили отрезки хорд MA, MB, MC, МД. Дополнив рисунок, сформулируйте по нему задачи, кто какие может.

Соедините А и С, В и D. Докажите, что CAB = CDB, АСМ= DBM.

Какое еще требование можно поставить к этому же условию?

Докажите, что Δ MAC ~ Δ MDB.

Какие следствия можно вывести из этого факта?

Примените свойства пропорций:

MA·MB=MC·MD

Сформулируйте полученную теорему (формулируется теорема так, как она приведена в учебнике).

Но у настоящего исследователя на этом изучение рассматриваемой ситуации не заканчивается. Так как хорды АВ и CD, проходящие через точку М, произвольны, то произведение МА • MB постоянно. Какой должен возникнуть у вас теперь вопрос?

Чему равно это произведение?

Чтобы ответить мы должны в рассматриваемой геометрической ситуации выделить постоянные величины, фигуры.

Выясняется, что здесь постоянными являются точки Q, М, а следовательно, и расстояние d между ними, радиус R окружности. Проведя хорду EF (диаметр) и применяя для нее доказанную теорему, получаем, что MA•MB=ME•MF=R²-d².

Предлагается переформулировать доказанную теорему.

Однако изучение вопроса пока еще полностью не закончено. Мы брали окружность (О, R) и точку М внутри ее круга. Как еще могут располагаться окружность и точка?

М принадлежит окружности (рис. 9 б); лежит вне круга (О, R)(рис 9 в).

Рассмотрим последний случай. Проведем хорды АВ и CD такие, чтобы МА и МС были секущими к окружности.

Спрогнозируйте зависимость между отрезками МА и MB, MC и MD. Учащиеся, используя аналогию, выдвигают гипотезу, что МА • MB = МС• MD, и доказывают этот факт. На вопрос учителя, чему же равно в этом случае каждое из произведений, были ответы, основанные на аналогии (МА • MB = R2 - d2, где d = ОМ), которые вызвали сразу же возражения части учащихся, заметивших, что в этом случае R2 - d2 < О и такого не может быть. После рассуждений получили, что МА • MB = d²-R²

Можно ли утверждать, что этот случай мы исследовали полностью?

Какие прямые, проходящие через точку М и связанные с окружностью, мы во втором случае можем провести, а в первом нет? (Касательные МТ и МТ₁).

Предлагается выяснить, связаны ли длины отрезков касательных с полученными величинами.В результате всех рассуждений приходят к формулировке теоремы: произведение секущей на ее внешнюю часть равно квадрату касательной.

В третьем случае МА • MB = MA•MM = 0. Учитель обращает внимание учащихся на то как меняется произведение МА • MB в зависимости от изменения положения точки М и данной окружности.

Подводится итог: К "открытию" новых фактов в математике можно прийти чисто дедуктивно. Логическим путем, прогнозируя результат на основе аналогии, рассматривая частные или все возможные случаи ка­кого-либо явления. Этими же приемами вы пользуетесь и для самостоя­тельного поиска решения задач.

Проведенный урок способствовал умственному развитию учащихся во всех его аспектах: получили новые факты-теоремы, учитель раскрывал методологию математики (законы и приемы познания математических закономерностей), развивал интеллектуальные качества ума (гибкость, критичность мышления и др.). Учащиеся весь урок работали с интересом. Заметим здесь, что это может быть лишь в том случае, если учащиеся приучены к постановке учителем проблемных вопросов и активно и с интересом включаются в поиск ответов на них.

К получению новых теорем школьники могут придти самостоятельно, формулируя предложения, обратные доказанным теоремам, и выясняя, являются они истинными или ложными.

В этой связи заметим, что изучение взаимно-обратных теорем важно вести одновременно, методом УДЕ, прибегая иногда для этого и к ре­конструкции последовательности изложения материала в учебнике.

Дедуктивный способ "открытия" теорем в. большей степени формирует дедуктивное, логическое мышление. Конечно, решая задачу, мы также делаем логические выводы из условия, но принципиальная разница в этих двух ситуациях заключается в том, что при решении задачи ученик знает требование, т. е. то, к чему должен придти, в отличие от первого случая:

Очень важным для интеллектуального развития школьников являются этапы поиска доказательства. При умело разработанной методике здесь имеются неограниченные возможности приобщения школьников к методам познания, как общим, так и частным, в и к естественной взаимосвязи: анализу и синтезу, сравнению и аналогии, индукции и дедукции.

Выше уже были примеры, когда в основе поиска доказательства лежит аналогия, неполная индукция. Однако чаше всего поиск ведется аналитическим, синтетическим или аналитико-синтетическим методами. Поскольку они достаточно подробно описаны в методической литературе, то мы на них останавливаться не будем.

При разработке технологии этапа доказательства теорем важно обучать школьников как общим логическим методам доказательств (1.2), так и частным приемам. Учителю важно учитывать новизну для учащихся метода или приема доказательства. Методика обучения школьников новому методу состоит в том, что после проведенного доказательства конкретной теорёмы учитель обращает внимание школьников на метод рассуждений, вместе с ними вскрывает особенности этого метода и проводит обобщение — выделяет сущность нового метода.

Например, в учебнике [10] теорема о выводе площади треугольника через две стороны и угол между ними доказывается с привлечением метода координат. На уроке, управляя поиском доказательства, учитель подвел детей к тому, что применяя известную формулу площади треугольника к выводу новой, нужно рассмотреть три случая: когда угол между данными сторонами тупой, прямой и острый. В каждом случае доказываемое предложение истинно. Следовательно, теорема верна для любого случая. Учитель вскрывает сущность доказательства, говорит, что метод, которым. ведется доказательство, называется полной индукцией. Разъясняется отличие полной индукции от неполной, задается вопрос: «Не приведете ли сами примеры теорем, которые доказывали методом полной индукции.» Учащиеся без труда назвали теорему о свойстве вписанного угла.

Еще один пример. Доказательство признака скрещивающихся прямых (если через одну из двух прямых проходит единственная плоскость, параллельная другой прямой, то такие прямые скрещиваются) проводится методом исчерпывающих проб. Для раскрытия его сути проводят следующие рассуждения

Как могут располагаться две прямые в пространстве? (Пересекаться, быть параллельными или же скрещиваться. Других случаев взаимного расположения двух прямых в пространстве нет. Предположим, что прямые пересекаются. Тогда нельзя через одну из них провести плоскость, параллельную второй прямой, так как последняя будет лежать в этой плоскости. Следовательно, этот случай невозможен.

Предположим, что прямые параллельны. Тогда через одну из них можно провести не одну плоскость, параллельную другой. Следовательно, этот случай также невозможен.

Поскольку возможны только три .случая взаимного расположения двух прямых на плоскости, и мы доказали, что два из них невозможны, то делаем вывод, что данные в условии теоремы прямые скрещиваются.

После проведенного доказательства проводится анализ метода доказательства, вскрывается его сущность и сообщается ученикам его название.

Заметим здесь, что рассмотренного признака скрещивающихся прямых нет в школьных учебниках. Однако если учитель целенаправленно осуществляет развитие школьников при обучении математике и четко осознает, что ему для этого следует делать, то при отборе материала, как теоретического, так и заданного, он будет стараться не упускать объективно заложенные в математическом содержании возможности.

Аналогично, на конкретных доказательствах, следует разъяснять сущность аналитического, синтетического методов доказательств, метода от противного, а также частных, специфических методов (метод геометрических преобразований, векторный метод в доказательстве теорем, приемы дополнительных построений, связанные с той или иной фигурой, ситуацией) и т. д.

На этапе осознания, осмысления происходит осознание (понимание) и запоминание как формулировки теоремы, так и ее доказательства. Управление этим этапом со стороны учителя осуществляется посредством специально сконструированной системы упражнений, заданий. Они должны носить как репродуктивный характер, так и развивающий. Приведем возможные типы заданий на этом этапе.

1. Сформулируйте доказанную теорему. Выделите условие, заключение.

2. Верно ли предложение: (учитель модифицирует формулировку, добавляя или опуская некоторые слова, которые а) изменяют смысл доказанной теоремы; б) не изменяют).

3. Создайте другой рисунок и обозначения к доказанной теореме (моделирование теоремы).

4. Проведите доказательство теоремы: а) с теми же обозначениями, но при новом расположении чертежа, б) при том же расположении чертежа, но в новых обозначениях.

5. Сформулируйте обратное (противоположное) утверждение.

6. Выделите основную идею (прием) доказательства.

7. Приведите примеры доказательства теорем или решенных задач, где бы использовался этот прием.

8. Составьте план доказательства теоремы (выделите основные эта­пы доказательства).

9. Выделите базис доказательства (опорные теоремы, аксиомы, опре­деления).

10. Найдите другой способ доказательства (возможны указания со стороны учителя).

11.Примените теорему к решению следующих задач (дается цикл дидактических задач на прямое применение, задачи с недостающими данными, с избыточными, где данные следует подкорректировать, прежде чем применить теорему).

12. Для решения каких задач можно использовать доказанную теорему (прогнозирование, составление эвристик)? Например: доказательство равенства углов, отрезков, параллельность прямых и т. д.

13. С помощью каких еще теорем можно решать указанные типы задач? (Перечисляются в этом случае все известные ранее способы и добавляется новый).

14. Составьте сами задачи на применение теоремы (на первых порах можно по готовому рисунку).

15. Опишите, как вы рассуждали, когда отыскивали: а) закономерность, отраженную в формулировке, б) доказательство.

Требования к системе упражнений на этапе применения теоремы от­ражены в п. 2. 3, где разговор пойдет уже об упражнениях.

Отметим, что отраженная в табл. 7 технология работы с теоремой, равно как и указанные выше виды заданий, на этапе осознания не может применяться при изучении каждой теоремы. Но она может служить основой для конструирования системы уроков с позиций развивающего обучения. В то же время ее реализация закладывает у школьников базу для самостоятельного решения как познавательных, так и развивающих задач.

В заключение опишем, как должен готовиться к уроку по изучению теорем учитель. Подготовка к уроку (или серии уроков) начинается с логико-математического и дидактического анализа ее формулировки и способа доказательства.

Логико-математический анализ предполагает выполнение учите­лем следующих учебных действий:

1 Анализ формулировки:

а) установление формы формулировки;

б) выделение условия, заключения, разъяснительной части;

в) установление того, является данное предложение простым или сложным;

г) выяснение возможности переформулировки сложной теоремы в виде двух простых теорем.

2. Выяснение логического смысла теоремы: существование, свойство, признак (критерий) понятия.

3. Формулировка обратного (противоположного) предложения и установление его истинности;

4. Диализ доказательства: выяснение идеи, методе, приема доказательства, установление их новизны для учащихся, отыскание других приемов доказательства.

5. Исследование математической ситуации, рассмотрение всех возможных случаев.

6. Установление связи теоремы с ранее изучению, ее роли в построении курса.

Дидактический анализ:

7.Выявление опорного материала и установление необходимости его повторения: методика организации повторения,

8. Установление необходимости мотивации изучаемой теоремы и подбор для нее соответствующего материала.

9. Возможность создания проблемной ситуации; набор способа (пути) создания проблемной ситуации.

10. Установление наличия у школьников базы знаний, том числе познавательных средств) для участия в разрешении проблемы с соответствующим уровнем самостоятельности.

11. Выбор гипотетико-дедуктивных методов, способов получения новых знаний: "открытие" теоремы; поиск доказательства; доказательство.

12 Установление возможности изучения обратной (противоположной) теоремы. Формулировка критерия понятия, переформулировка его определения.

13. Выбор формы записи доказательства, а ТЯВД» установление необходимости записи доказательства

14. Установление возможности обучения новому ЧМОДУ доказательства.

15. Подбор системы упражнений для этапов "осознание, осмысление, применение".

ЛЕКЦИЯ № 4. ТЕХНОЛОГИЯ ОБУЧЕНИЯ МАТЕМАТИЧЕСКИМ ПРАВИЛАМ (4 часа)

Понятие правила

Математическое правило представляет собой описание общего способа решения однотипных стандартных задач.

Приведем примеры правил из различных школьных учебников.

1 Умножение десятичных дробей выполняется по следующему пра­вилу:

а) не обращая внимания на запятые, выполнить умножение натуральных чисел;

б) в полученном результате отделить справа запятой столько десяти­чных знаков, сколько их содержится в обоих множителях вместе.

2. Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа: (а – b)² = а² - 2ab + b².

3. Косинус суммы двух аргументов равен: cos( α+ β) = cosα cosβ - sinα sinβ.

4. Для нахождения наибольшего и наименьшего значений непрерывной и дифференцируемой функции f(x) на отрезке [а, b] нужно:

а) найти значения функции на концах отрезка, т. е. числа f(а) и f(b);

б) найти ее значения в стационарных точках, т. е. в тех точках инте­рвала (а, b), где производная равна нулю;

в) из найденных значений выбрать наибольшее и наименьшее.

5. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертежный угольник к прямой а, а к нему линейку. Затем, продвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника, и проведем искомую прямую b.

6. Чтобы построить точку пересечения данной прямой с заданной плоскостью, надо сначала найти в этой плоскости такую прямую, которая бы с данной прямой лежала в некоторой плоскости, а затем найти точку пересечения этих прямых.

7. Чтобы построить биссектрису данного угла А, надо провести окружность произвольного радиуса с центром в вершине А данного угла.

Она пересечет стороны угла в точках В и С. Затем проведём две окружности одинакового радиуса ВС с центрами в точках В и С. Они пересе­кутся в двух точках. 'Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Тогда луч АЕ является биссектрисой данного угла А.

8. Корни квадратного уравнения ах² + bx+c=0 вычисляются по

формуле: , где D =b²-4ac≥0.

9. Правило сравнения двух чисел:

-Число а больше числа b, если разность а-b положительна.

-Число а меньше числа b, если разность а-b отрицательна.

-Число а равно числу b. если разность а-b равна нулю.

Проведенный анализ правил, изучаемых в курсе математики, позволяет сформулировать следующие выводы (а приведенные примеры правил иллюстрируют некоторые эти выводы):

• в школьных учебниках много правил,

• значительное число правил содержит курс алгебры в отличие от курса геометрии;

• правила излагаются в различных формах: словесной (примеры 1, 4-7, 9); символьной (примеры З, 8); словесной и символьной (пример 2);

• отдельные правила (пример 4) представляют собой четкую последовательность шагов для решения стандартных задач определенного типа (в этом случае будем говорить что правило задано в форме алгоритма);

• решение однотипных задач значительно облегчается, если правило имеет форму алгоритма (заметим, что в школьных учебниках далеко не каждое правило имеет такую форму);

• обычно каждое последующее-правило включает в Себя отдельные ранее изученные правила (например, правило нахождения наибольшего и наименьшего значений функции fix) на отрезке (пример 4) включает в себя правило нахождения стационарных точек):

• за каждым правилом легко просматривается его теоретический базис, т. е. математическая основа, которая может состоять или из одной теоремы (такие правила Л. М. Фридман, Е. Н. Турецкий [47] называют правилами-теоремами, или правилами-тождествами, или правилами-формулами (см. соответственно примеры 5, 2 и 3, 8), или из одного определения (правило-определение, см. примеры 4 и 9), или их сочета­ния (см примеры 1,6 и 7));

• •многие правила нужно самостоятельно извлекать из соответствую­щих теорем (тождеств, формул) и определений (см. пример 6),

При решении нестандартной задачи мы применяем несколько правил. Следовательно, от усвоения обучаемыми правил зависит успех решения задач.

Наблюдая за деятельностью учителей на уроках математики, мы замечаем довольно часто такую последовательность изучения правила: повторение изученных правил → сообщение учащимся нового правила в готовом виде (обычно в той форме, в какой оно представлено в школьном учебнике) → образец решения 2-3 упражнений по данному правилу → выполнение заданий из учебника (как правило, присутствует фронтальная форма организации учебной деятельности обучаемых).

При таком подходе все усилия учителя направлены в основном на усвоение информационной компоненты содержания правила. Таким образом, учитель строит свои действия и действия школьников в рамках объяснительно-репродуктивного типа обучения, в котором отводится довольно пассивная роль учащимся.

Представленная ниже технология обучения правилам соответствует общим положениям, развиваемым в психологической теории учебной деятельности, где ученик "... выступает как ее подлинный субъект, проя­вляя инициативу и самостоятельность в принятии и решении учебных задач [13, с. 185]. Схематично данная технология представлена в табл. 8.

ЭТАПЫ ИЗУЧЕНИЯ ПРАВИЛ

I. Подготовка к восприятию

Цель первого этапа: актуализация опорных знаний, умений, необхо­димых для введения и обоснования правила, а также формирование положительной мотивации его изучения.

Основным средством актуализации являются упражнения. На этом этапе более эффективна индивидуальная работа учащихся с последую­щей фронтальной проверкой. Выполнение известных учащимся заданий создает ситуацию успеха для изучения нового.

Приведем примеры

1. Для правила умножения десятичных дробей:

а) Выразите в мм: 93,2 см; 4,8 см;

б) Представьте в см² число 44736 мм²;

в)Сколько десятичных знаков в следующих числах: 447,36; 44,736; 0,5; 1; 34; 0,009?

г) Найдите площадь прямоугольника со сторонами а = 32 см и в = 25 см.

2. Для правила квадрата разности двух чисел:

а) Раскройте скобки: (2m³)², (-4a²b)², , (3n²)² ;

б) Представьте в виде квадрата двучлена, если это возможно:

y⁴, 16а², 9аb², 4m⁶ , 9n⁴;

в) Упростите: 2m²n³·m³n²; 5p⁵·0,2pr; 2·2m³·3n²;

г) Представьте в виде удвоенного произведения двух одночленов:

6ab, 10x²y, 0,5p, 12n²m³.

Заметим, что готовность к восприятию отдельных правил не всегда есть кратковременный этап, он может быть растянут на несколько уроков. В этом случае говорят, что имеет место опережающее обучение.

Таблица 8

Технология обучения правилам

Актуализация опорных знаний и умений

Мотивация (проблемная ситуация)

Постановка учебной задачи

Решение учебно -исследовательской задачи

Выделение обобщенного способа действия

Фиксация его в виде различных записей (схем, чертежей и т.д.)

Решение упражнении Содержание упражнений соответствует принципам: полноты, однотипности, контрпримеров, сравнения, непрерывного повторения, единственного различия, вариативности

Последовательность деятельности: соответствует принципам: от простого к сложному, цикличности

Изучение теоретичес-

кого мате-

риала

Решение задач

Так, правила, основанные на формулах сокращенного умножения, требуют достаточно длительной пропедевтики, связанной с переводом словесной модели в символьную и обратным переводом. Поэтому за несколько уроков до изучения формул сокращенного умножения полезно включать в устную работу такие упражнения:

1. Даны два выражения 2х и 3у. Запишите: квадрат первого, куб второго, квадрат их разности (суммы), разность (сумму) их квадратов, уд­военное их произведение, утроенное их произведение и т. д.

2. Прочитайте данные выражения:

p² -(2q)² ; (p-2q)²; (р+ 2q)² ; р2 + (2q)² ; 2· р2· 2q; 3р² · 2q и т.д.

От урока к уроку выражения усложняются.

Эффективным средством формирования положительной мотивации для изучения нового правила является создание проблемной ситуации.

В качестве проблемных ситуаций к рассматриваемым правилам могут служить следующие задачи:

1) Вычислить площадь прямоугольника со смежными сторонами

а= 93,2 см и b = 4,8 см;

3. Найти значение выражения:

Ученики понимают, что площадь прямоугольника можно найти действием умножения данных чисел 93,2 и 4,8 (вот почему перед этим было предложено аналогичное задание с натуральными числами), однако им неизвестен способ умножения десятичных дробей. Теперь целесообразно предложить учащимся сформулировать тему урока и его цели.

Аналогично возникает проблемная ситуация и во втором случае. Ученикам ясно, что данное числовое выражение имеет значение, но известные им способы приводят к громоздким вычислениям. Естественно, возникает потребность в поиске другого способа нахождения значения выражения.

II. Восприятие

Цель второго этапа: "открыть" совместно с учащимися новое правило.

В школьной практике наравне с сообщением учащимся нового правила в готовом виде наблюдается и вариант его введения путем обобщения частных случаев.

Так, изучая тему "Вынесение общего множителя за скобки", учителя предлагают выполнить группы упражнений:

1. 2m + 2n, 8 —4х ... (вынесение общего числового множителя),

2. ах- aу, cd + bc... (вынесение общего буквенного множителя),

3) 9a²b—12ab³ ... (вынесение общего числового и буквенного множителя);

4) 6рк -Зр... (после вынесения общего множителя появляется "1") и т. д.

После их решения формулируют правило. Известный психолог В. В. Давыдов так оценивает этот путь: "... имея дело с частными зада­чами, школьники овладевают столь же частными способами их реше­ния (лишь в процессе тренировки учащиеся усваивают некоторый об­щий способ их решения) Усвоение этого способа происходит путем перехода мысли от частного к общему" [13, с. 158]. В. В. Давыдов пред­лагает принципиально иной путь формирования у школьников обобщенного способа решения однотипных задач, в ходе которого у них развивается теоретическое мышление в отличие от эмпирического. Суть этого подхода заключается в следующем. Ученикам предлагается учеб­ная задача, основной целью которой является обнаружение, "открытие" обобщенного способа решения однотипных задач. Совместно с учителем они решают ее, затем анализируют условие и решение, отвлекаясь при этом от частных ее особенностей. В результате анализа, абстракции появляется искомый способ решения. Образно этот путь В. В. Давыдов называет обобщением "с места". Оба эти пути представлены в виде следующих схем:

I путь II путь

Обобщенный способ к.п.з к.п.з к.п.з

Частный Частный Частный Обобщенный способ

способ способ способ

к.п.з к.п.з к.п.з учебная зада

к.п.3 — конкретная практическая задача.

Замечаем, что важнейшим компонентом учебной деятельности является "учебная задача". В. В. Давыдов так ее трактует:

"Учебная задача требует от школьников: 1) анализа ее условий с целью обнаружения в них некоторого общего отношения, имеющего закономерную связь с различными его проявлениями, т. е. построения содержательной абстракции и содержательного обобщения; 2) выведения на основе этой абстракции и этого обобщения некоторых частных отношений и их объединения (синтеза) в целостный объект, т. е. построения его "клеточки" и мысленного конкретного объекта; 3) овладения в этом аналитико-синтетическом процессе общим способом мысленного построения изучаемого объекта" [13, с. 157-158].

Сторонники теории поэтапного усвоения умственных действий утверждают, что необходимым компонентом любого нового действия является ориентировочная основа — та система операций, на которую реально опивается человек при выполнении действия. Она должна быть правильной, полной и материализованной в виде различных записей, схем, чертежей и т. д. "Ее образование есть главная задача и главное содержание первого этапа формирования действия" [48, с. 81].

Особое внимание психолог П. Я. Гальперин обращает на ориентировочную основу, тип которой характеризуется полнотой, высоким уров­нем обобщения, а главное — учащиеся сами участвуют в ее создании,

т. е. этот тип ориентировочной основы действий и учения связан с пере­ходом учащегося к теоретическому мышлению.

Итак, этап восприятия схематично можно представить в следующем виде: постановка учебной задачи (т. е. постановка перед учащимися задачи о выделении обобщенного способа действия) - решение учебно-исследовательской задачи -> выделение обобщенного способа действуя -> фиксация его в виде различных записей, схем, чертежей и т. д. (см. табл. 8).

Проиллюстрируем этап восприятия для рассматриваемых выше двух правил.

1. Учитель предлагает найти способ умножения десятичных дробей, вычислив площадь прямоугольника, если его стороны выражены деся­тичными дробями. В частности, а = 93,2 см, b = 4,8 см.

В этом задании одна часть кажется ученикам известной — надо най­ти произведение сторон. Затруднение только в том — как перемножить десятичные дроби (93,2 х 4,8).

• А что вас смущает? (Нет правила умножения десятичных дробей; не знаем, как подписать одно число под другим — это было важно при сложении: не знаем, где поставить запятую, если перемножить их как натуральные числа).

• Можно ли свести задачу к известной и как это сделать? (Можно, если перейти к другой единице измерения, например к мм)..

•Итак, первый шаг: 93,2 см = 932 мм, 4,8 см = 48 мм. Сформулируйте его словесно (выбрав другую единицу измерения, перейти к натуральным числам).

•Второй шаг: найти произведение натуральных чисел, тогда площадь равна 932 х 48 = 44736 (мм²).

• Третий шаг: выразить результат в см² (447,36 см²).

• Сравните записи: 93,2 см х 4.8 см и 447,36 см².

• Таким образом, мы получили правило вычисления площади прямоугольника, стороны которого не являются натуральными числами. Поможет ли это нам в решении главной задачи — как умножить десятичные дроби, например 93,2 х 4,8?

Возможны различные ответы учащихся Например, считать эти числа длинами сторон прямоугольника, измеренными одной и той же единицей, затем увеличить единицу измерения в десять раз, перейти к натуральным числам и т. д.

Учитель тут же реагирует на данное предложение, записывая контрпример (9,3 х 0,48), не приводящий к нужному результату по приведенному учеником правилу.

Итак, одну особенность правила умножения десятичных дробей вы уловили: Действительно, перемножать надо числа как натуральные. Вернемся к записи: 93,2х 4,8 - 447,36; Осталась не вскрыта еще одна особенность. На что надо обратить внимание? (На число десятичных знаков в каждом из множителей и в произведении, в каком направлении следует отделять нужное число десятичных знаков в произведении).

По ходу беседы учитель ведет записи в две колонки: слева — выполненные операции, справа — их словесное описание в виде указаний- инструкций. Таким образом получаем правило умножения десятичных дробей в форме алгоритма. Эта форма особенно полезна слабоуспевающим учащимся.

1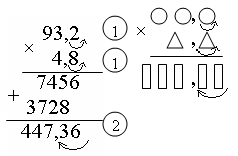 ) записать один множитель под другим, не обращая внимания на запятые;

2) выполнить умножение чисел как натуральных;

3) определить число десятичных знаков в обоих множителях;

4) отделить это число знаков в полученном произведении справа налево.

На этапе открытия обобщенного способа действия предпочтение следует отдавать групповой форме обучения, которая непосредственно влияет на развитие рефлексивных способностей учащихся.

2. После создания проблемной ситуации (найти значение выражения с. 59) учитель предъявляет учащимся такое задание:

•Представьте в виде многочлена следующее выражение:

(2m³ + 3п²)².

Задание доступно ученикам, постепенно появляется следующая запись: (2m³ + Зn²)² = (2m³ + Зn²)(2m³ + Зn²) = 4m⁶ + 6n²m³ + 6m³n² + 9n⁴

или

(2m³ + Зn²)² = 4m⁶ + 12m³n² + 9n⁴,

• • Как получить многочлен, записанный в правой части равенства, непосредственно из выражения, расположенного слева, минуя промежуточные выкладки? Попытаемся совместно найти ответ на этот вопрос.

• Прочитайте выражение в левой части равенства.

• Установите связи между одночленами:

2т³ и 4m⁶; 3п^г и 9n⁴; Зn² и 12rn³n².

В ходе анализа, абстрагирования и обобщения появляется запись (I + П)²=I²+2·I·П + П²,отражающая правило о квадрате двучлена.

Отметим различные материализованные формы правил: в виде алгоритма и в виде схемы. Возможна и другая форма: текст правила разби­вается на части, соответствующие той или иной операции, части отде­ляются одна от другой вертикальной чертой: Например, квадрат суммы двух чисел | равен квадрату первого числа | плюс удвоенное произведе­ние первого числа на второе | плюс квадрат второго числа [12, 37]. Каж­дое правило желательно фиксировать в одной или нескольких формах, которые могут быть вынесены на плакат, кодопозитив, в отдельную тетрадь—справочник учащегося.

Теперь легко просматриваются цели большинства заданий, предложенные на этапе готовности к восприятию.

Очевидно, что описанный этап восприятия потребует, особенно вначале, несколько больших затрат времени. Однако эти затраты окупаются, как показывает опыт, формированием положительных характеристик действия, а именно правильностью, большей самостоятельностью, устойчивостью, обобщенностью, а также способностью к переносу умения на новые ситуации.

III. Осознание, осмысление

Цель работы учащихся на третьем этапе: осознать, осмыслить правило при решении различных дидактических задач, а также его запомнить.

Очевидно, основным средством обучения на этом этапе служит сис­тема упражнений

Наибольшую трудность, особенно для начинающего учителя, пред­ставляет разработка системы упражнений. Действительно, на. уроках нередко наблюдаем такую картину, особенно характерную для уроков алгебры: после введения правила учитель указывает список упражнений из учебника для классной работы, например, под четными номерами, для домашней — под нечетными. Заметим, что такой подход к выбору упражнений рекомендуют авторы многих методических пособий. Как правило, учитель использует при этом фронтальную форму организации учебной деятельности.

При первом взгляде обстановка на уроке вполне нормальная, как будто каждый ученик занят выполнением упражнений. Однако более пристальные наблюдения позволяют выделить разные группы ребят. Одни переписывают, едва успевая за теми, кто работает у доски. Другие, у кого быстрая реакция и неплохо обстоит дело с техникой вычисления, после фронтального выполнения первого задания на доске механически переносят идеи его решения на серию однотипных упражнений. Дойдя до нового вида задания, они начинают испытывать затруднения, но даже не пытаются напрячь свои умственные силы, так как знают, что скоро появится его решение на доске. Затем они опять быстро выполняют серию однотипных упражнений и т. д. Третьи, у кого обычно завышена самооценка, "ускакали" вперед, совершив порой грубые ошибки. Все призывы учителя сверить свое решение с записями на доске обходят их стороной, И лишь небольшая группа ребят самостоятельно выполняет упражнения в своем темпе, сверяя свои ответы с результатами, которые постепенно появляются на доске.

Порой возникает и такая ситуация. Учитель запланировал опреде­ленное число упражнений, но оно оказалось явно завышенным. Тогда учитель, чтобы успеть выполнить намеченное, начинает торопить ребят или переносит часть упражнений (в конце урока они обычно сложнее) в домашнее задание.

Такая картина, думаем, знакома многим. В связи с этим необходимо обсудить следующие вопросы:

1. Каково должно быть содержание упражнений?

2. Какова при этом последовательность их выполнения?

3. Какие спланировать организационные формы выполнения упражнений?

Попытаемся ответить на эти вопросы, опираясь на исследования Я. И. Груденова, Г. И. Саранцева [12, 37] по проблеме построения и реализации системы упражнений в обучении математике.

При отборе содержания упражнений учителю следует руководствоваться определенными принципами, а именно: полноты, однотипности, контрпримеров, сравнения, непрерывного повторения, вариативности, единственного различия.

Дадим краткую их характеристику и проиллюстрируем на примере правила умножения десятичных дробей.

Принцип полноты. Система упражнений удовлетворяет принципу полноты, если она содержит все виды заданий на данное правило, включая и особенные случаи.

Так, в соответствии с этим принципом упражнения на правило умножения десятичных дробей должны содержать четыре вида заданий: 1) цифр в произведении достаточно для отделения десятичных знаков; 2) не хватает цифр для целой части; 3) не хватает цифр для целой и дробной части; 4) умножение десятичной дроби на натуральное число.

Вполне очевидны последствия несоблюдения принципа полноты. К сожалению, в учебниках не всегда реализован этот принцип.

Принцип однотипности. На каждый вид задания должно быть не одно упражнение. Отметим, что однотипные упражнения особенно не­обходимы для слабых учеников и в меньшей мере для сильных. После­довательное выполнение однотипных упражнений приводит к снижению активности мыслительной деятельности учащихся, так как при решении лишь первого примера они опираются на соответствующее правило.

Значит, на каждый из четырех видов (см. предыдущий пример) учи­тель должен подобрать достаточное число однотипных упражнений, ориентируясь на уровни развития учащихся класса.

Принцип контрпримеров. Контрпример — это любая задача, которая провоцирует учащихся на ошибку. Соблюдение этого принципа ведет к воспитанию положительной мотивации и вместе с тем способствует углубленному пониманию правила. Я. И. Груденов по этому поводу пишет: "В тех классах, где контрпримеры начинают использовать систематически, они воспринимаются учащимися как своеобразная игра, в которой побеждают более внимательные и сообразительные" [12, с. 157].

Заметим, что многие учебники практически не содержат заданий, провоцирующих учащихся на ошибку. Значит, учителю нужно самому подбирать или создавать такие упражнения. Приведем пример упражнения, которое соответствует обсуждаемому принципу.

Определите, в каких примерах допущены ошибки, если известно, что

72 · 37 = 2664:

1) 7,2·0,37 = 266,4;

2) 7,20 · 0,37 = 0,2664;

3) 0,072·370 = 2,664;

4) 0,720 · 370 = 26,64.

Принцип сравнения. Применение этого принципа предполагает включение некоторого ряда взаимосвязанных упражнений, когда хотят подчеркнуть их сходство или различие, в частности упражнения на пря­мые и обратные операции, действия.

Классическим примером может служить совместное решение задач следующих трех видов: 1) нахождение процентов от числа, 2) нахожде­ние числа по его проценту; 3) нахождение процентного отношения.

Вернемся к нашему правилу:

Поставьте запятую во втором множителе так, чтобы равенство было верным: 0,52•167 = 8,684.

Здесь ученикам придется выполнять обратную операцию: из числа десятичных знаков произведения вычитать число десятичных знаков первого множителя.

Принцип непрерывного повторения. Система упражнений содер­жит задачи из предшествующих разделов. Цель их включения: во-первых, осуществлять систематическое повторение изученных действий, особенно тех, при выполнении которых учащимися допускаются ошибки, во-вторых, устранять отрицательное влияние однотипности упражнений (ослабление внимания, снижение интереса и т. д.).

Обратимся к показательному примеру — правилу умножения одно­членов. Полезно, например, в такие упражнения, как: -a²·(-а²); 5х³·(-Зх³); b ·b и т. д., включать упражнения на сложение одночленов: -а² -а²; 5х³ + (-Зх³); b+b и т. д. Заметим, что последние примеры соответствуют одновременно и принципам контрпримеров, и сравнения.

Пример. Найти сумму двух чисел 6,09 и 3,1.

Принцип вариативности. Этот принцип реализуется двояко: с одной стороны, видоизменение формы выдачи заданий, с другой — разнообразие числовых и буквенных компонентов алгебраических выражений, а в упражнениях по геометрии варьирование рисунков и обозначений.

Так, в учебнике [30] даны 34 упражнения на правило умножения десятичных дробей с одной формулировкой задания: вычисти.

Полезно учащихся включать в игру "Кто больше придумает формулировок заданий к примеру: 0,720 • 370 = 266,4?": 1) вычислить; 2) найти значения

числового выражения; 3) найти произведение; 4) число 0,72 увеличили в 370 раз, найдите число после увеличения; 5) выполнить умножение и т. д.

Принцип единственного различия. Сущность этого принципа заключается в сохранении всех элементов формы упражнений при переходе от одного упражнения к другому, кроме одного.

Пример. Если проанализировать все операции, входящие в правило умножения Десятичных дробей, то новой является подсчет числа десятичных знаков в произведении. Следовательно, надо отобрать группу упражнений на осмысление этой операции. После заданий на вычисление произведения чисел 4,302 и 5,6 сразу же предлагаем серию упражнений с "плавающими" запятыми: а) 4,302•56; б) 4,302•0,0056; в) 4,302•0,0056.

Заметим, что не надо формально подходить к отбору содержания упражнений. В зависимости от новой темы, цели урока и других соображений учитель может реализовать не все принципы, в особенности принципы непрерывного повторения и сравнения, а иногда одно упражнение, как было замечено выше, удовлетворяет нескольким принципам.

Опираясь на вышеуказанные принципы, учитель отбирает упражнения на осознание, осмысление того или иного правила.

Теперь встает проблема их упорядочивания.

Очевидно, надо исходить из принципа от простого сложному. Раскрывать его содержание не будем, так как само название говорит за себя.

Еще одним важным принципом для компоновки последовательности упражнений служит принцип цикличности.

Чтобы понять его важность, обратимся опять к теории поэтапного формирования умственных действий [43, 48].

Этап восприятия закончился выделением ориентировочной основы действия в материализованном виде (разные формы записей обобщенного способа действия). Чтобы новое действие было усвоено, оно должно перейти из внешнего плана во внутренний, преодолевая ряд этапов:

1. выполнение действия в материальном или материализованном виде;

2. формирование действия как внешнеречевого (в форме громкой речи);

3. формирование действия во внешней речи про себя;

4. выполнение действия в умственном плане.

Каждому этапу соответствует определенный цикл упражнений, который в первую очередь удовлетворяет принципу полноты. Там, где разумно, при подборе упражнении первого цикла учитывают принцип един­ственного различия, при подборе упражнений других циклов — либо принцип контрпримеров, либо принцип непрерывного повторения, либо принцип сравнения. Следовательно, однотипные упражнения находятся в разных циклах. При переходе от цикла к циклу сложность упражнений возрастает, порядок упражнений внутри каждого цикла нарочито меняется.

В соответствии с вышеперечисленными принципами построим сис­тему упражнений для этапа осознания, осмысления правила умножения десятичных дробей:

I цикл

Выполните умножение, сопоставляя каждое свое действие с записанным правилом: 1) 4,302•5,6. 2) 4,302•56, 3) 4,302•0,056; 4) 4,302•0,0056.

II цикл

Вычислите; вслух обоснуйте каждый свой шаг, опираясь на правило:

1) 6,17 ·0,034; 2) 0,056 · 1,05; 3) 0,72 · 37; 4) 6,09 + 3,1.

/// цикл (работа в парах: объясните друг другу решение; правило зак­рывается)

1. Поставьте запятую в произведении: 0,67•120 = 804;

2. Поставьте запятую во втором множителе: 0,52•167=8,684;

3. Поставьте запятые в обоих множителях: 10003•6 = 6,0018.

IV цикл (индивидуальная работа с последующей проверкой) Определите, в каких примерах допущены ошибки, если известно, что

72•37 = 2664: 1) 7,2•0,37 = 266,4; 2) 7,20•0,37 = 0,2664; 3) 0,072•370 = 2,664;

4) 0,720•370 = 26,64.

Заметим, что структурирование упражнений по циклам позволяет учителю чувствовать себя на уроке более комфортно, на него не давит так временной аспект, как при традиционном подходе к упражнениям.

К числу циклов не надо подходить формально, на осознание некото­рых правил в отдельных классах достаточно бывает и трех циклов, ино­гда их число больше. Кроме того, не всегда все циклы удается реализо­вать на одном уроке.

Теперь перейдем к обсуждению форм организации учебной деятельности учащихся.

При выполнении упражнений первого цикла, очевидно, целесообраз­но использовать фронтальную форму работы, так как каждое упражне­ние цикла имеет свои особенности. Получив первое упражнение цикла (например, 4,302•5,6), ученик прочитывает вслух первую операцию, входящую в состав действия (записать данные множители, не обращая внимания на запятые), выполняет ее (4302•56), затем переходит ко второй операции и так до тех пор, пока не выполнит все записанные операции.

Решение упражнений второго цикла полезно вести с комментированием, что дает возможность учителю осуществлять пооперационный контроль за действиями учащихся.

Упражнения третьего и четвертого циклов учащиеся могут выполнять в парах или самостоятельно. Конечно, здесь требуется оперативная проверка результатов их работы. На этих этапах правило закрывается, работа идет по памяти, происходит интериоризация действия во внутренний план.

Заметим, что там, где возможно, надо прибегать к творческим домашним заданиям. Приведем для примера два варианта таких заданий.

1. Составить примеры на правило умножения десятичных дробей на каждый случай, т. е. четыре примера.

2. Составить краткий справочник возможных ошибок при умножении десятичных дробей.

В отличие от обычного домашнего задания здесь мало рутинной работы, есть возможность проявить, оригинальность, самостоятельность, выдумку. Кроме того, оно индивидуально. В классе появляется атмосфера состязательности, что еще полнее мобилизует волевые умственные и эмоциональные силы учащихся.

Как показывает практика, у школьников, которые обучались по дан­ной технологии, формировалась корректная математическая речь, они непроизвольно запоминали правила, им не нужно было большого числа упражнений на их усвоение.

Отметим, что много вычислительных правил сосредоточено в курсе математики V-VI классов, — явно больше, чем других дидактических единиц. Следовательно, от качества усвоения правил и умственного развития учащихся при этом, а именно на это нацелена описанная технология, будет зависеть далее успех изучения курса, математики в целом.

В заключение сформулируем диагностируемые учебные цели при изучении правила на уровнях "знание", "понимание" и "применение" и опишем критерии их достижения через наблюдаемые действия учащихся (табл. 9) в соответствии с вышеизложенным материалом п. 1.1.

Таблица 9

Диагностируемые учебные цели при изучении правила

Категории учебных целей	Критерии достижения целей
	Цель считается достигнутой, если ученик:
1.Знание	— воспроизводит формулировку правила в той форме, в которой оно было получено при изучении: —вставляет пропущенные слова в формулировке; — выбирает верную формулировку среди предложенных
2.Понимание	— раскрывает смысл правила своими словами; восстанавливает последовательность нужных действий в соответствии с правилом из предложенного набора действий (который может быть И избыточным); переводит формулировку правила с естественного языка на символический или графический и обратно; выделяет последовательность действий в соответствии с правилом, если оно не было сформулировано при изучении в алгоритмической форме; указывает теоретический базис правила; выбирает среди предложенных упражнения, решаемые с помощью данного правила; выделяет среди предложенных ситуации, в которых применимо правило, но в явном виде оно не задано; составляет задания на применение правила
3.Применение	—выполняет действия по правилу; —применяет правило к решению конкретного цикла упражнений, соответствующих принципу полноты; —обнаруживает ошибки в упражнениях с "ловушками"; —составляет краткий справочник с возможными ошибками

ЛЕКЦИЯ № 5. РАБОТА НАД ЗАДАЧЕЙ В СИСТЕМЕ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ (2 часа)

ПОНЯТИЕ «ЗАДАЧА»

Термин "задача" широко используется ив жизни, и в различных науках, и в учебных дисциплинах: психологии, логике, педагогике, математике, физике и т. д. Этим термином обозначаются многие и разные понятия. Поэтому очень трудно дать общее определение понятия "задача".

К задаче тесно примыкают понятия "вопрос", "упражнение", "проблема". Анализ различных подходов к соотношению между этими понятиями и к описанию их содержания дан, например, в работах Л. М. Фридмана и Г. И. Саранцева [46, 37]. Содержание понятий "задача" и "упражнение", роль и функции задач в обучении математике и развитии учащихся детально раскрыты в монографиях Ю. М. Колягина Л. М. Фридмана, Г. И. Саранцева и др. [18, 46, 37].

В данном случае термин "задача" будем понимать в широком смысле: упражнение, задание, которые нужно выполнить, или вопрос, на который нужно найти ответ, опираясь на указанные условия. Таким образом, любая задача состоит из двух частей: условие, т. е. исходные данные, и заключение, т. е. требование, которое нужно выполнить.

Роль задач в обучении и развитии школьников хорошо просматривается в технологиях работы с определением, теоремой, правилом. В самом деле, актуализация знаний на этапе подготовки к восприятию предпочтительна в ходе решения задач. Проблемная ситуация также чаще всего возникает в результате выполнения упражнений и решения задач. Даже на этапе организации восприятия возможно использование задач. Осознание, осмысление вводимых дидактических единиц осуществляется главным образом в процессе выполнения упражнений определенных типов, системы упражнений, построенной с соблюдением ряда принципов (см. пп. 2.1., 2.2, 2.3).

На этапах подготовки к восприятию, восприятия, осознания и осмысления в работе над основными дидактическими единицами упражнения и задачи выступают как средство изучения математики. Здесь, как правило,

используются несложные одно-двухшаговые задачи и упражнения. Их принято называть дидактическими. Дидактическая задача может выполнять развивающие функции. При их решении формируются и эвристические, и логические, и речевые умения.

Вместе с тем задача — это и цель изучения математики. Математику изучают и для того, чтобы научиться решать задачи.

Почему так важно уметь решать задачи?

Анализ деятельности по решению задач разных типов показывает, что приемы и методы познания, которые осваиваются в процессе изучения определений, правил, теорем, постигаются и в процессе работы над задачей. Однако, в освоении познавательных средств в процессе решения задач есть своя специфика: на этапах поиска решения и анализа решения задачи методы познания, приемы и способы мышления осваиваются в процессе их самостоятельного творческого применения. Определение, правило, теорему, аксиому или вводит учитель, или учащиеся читают их формулировки по учебнику, или они возникают в ре­зультате совместной деятельности учителя и учащихся при ведущей роли учителя. Задачу же в идеале каждый ученик должен решать сам, выполняя, например, домашнюю работу, самостоятельную, контроль­ную, экзаменационную и другие работы. Именно потому, какие задачи и как ученик решает самостоятельно, мы судим о его умственных способностях, о направленности его мышления, об уровнях усвоения знаний.

Однако умение решать задачи самостоятельно, без посторонней помощи формируется автоматически, непроизвольно лишь у небольшой части учащихся. Для большинства же требуется специальная работа учителя в этом направлении. Необходимо учить школьников решать задачи, думать над задачей.

Обучению учащихся решению задач посвящены специальные исследования Д. Пойа, Л, М. Фридмана и Е. Н. Турецкого, Г. И. Саранцева и других авторов [32, 47, 37]. Осветим эту проблему в связи с разработкой технологии развивающего обучения математике.

На этапе осознания, осмысления в работе с определением, теоремой, правилом, как было отмечено, решаются дидактические задачи, т. е. одно-двух шаговые задачи на прямое применение изучаемой теории. Далее осуществляется этап закрепления, применения. Границу между последними двумя этапами провести довольно трудно. Формально можно сказать, что на этапе закрепления, применения решаются задачи, в которых изучаемая дидактическая единица используется в совокупности с другими дидактическими единицами этой и ранее изученных тем. Постепенно осуществляется переход к более сложным задачам, которые могут быть сформулированы и не в терминах данной темы.

Приведем примеры задач, решаемых на этапе закрепления, применения.

1. Формула разности квадратов

1. Разложить на множители

а)(а + 2b)²-9a²;

6)(2a+b)²-(2b+a)².

1.2. Решить уравнение

(Зх+ 1)(3х +1) - (Зх - 2)(2 + 3х) = 17.

2. Доказать, что при любом натуральном п число

(7 п + 1)² -(2 п - 4)² делится на 15.

2. Определение: число а больше (меньше) числа b. Доказать, что при любых значениях а верно неравенство (3a-2)(a + 2)<(1 + 2a)².

3. Площадь треугольника

Две стороны треугольника равны- 7,5 см и 3,2 см. Высота, проведенная к большей стороне, равна 2,4 см. Найти высоту, проведенную к меньшей из данных сторон.

4. Подобные треугольники

В треугольнике ABC (AB ≠ АС) через середину стороны ВС проведена прямая, параллельная биссектрисе угла А, которая пересекает прямые АВ и АС соответственно в точках D и Е. Доказать, что BD = СЕ.

Если проанализировать решения этих задач, то можно заметить, что для решения задач 1.1 и 1.2 достаточно применить формулу разности квадратов и известные учащимся способы упрощения выражений и решения уравнений вида ах = b. Задачи 1.1 и 1.2 — примеры стандартных задач. Если задачи 2 и 3 решать первыми среди задач такого типа, то здесь последовательность элементарных шагов, составляющих реше­ние, нужно отыскивать. Однако последующие задачи таких типов стано­вятся стандартными. Математические задачи, для решения которых в школьном курсе математики имеются готовые правила (в любой форме) или эти правила непосредственно следуют из каких-либо определений или теорем, определяющих программу решения этих задач в виде по­следовательности шагов, принято называть стандартными. Нестандартные задачи — это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения [47, с. 43,48}. Задачи 1.3 и 4 - примеры нестандартных задач.

Четко отделить стандартную задачу от нестандартной на практике не всегда возможно. Показательна в этом плане ситуация с задачами 2 и 3. Рассмотрим еще следующую задачу: Доказать, что при любых а и b верно неравенство a² +b² + 1>ab+b + a. На первый взгляд, имеем стандартную задачу на доказательство неравенств. Однако оценка раз­ности между левой и правой частями этого неравенства — задача не­стандартная, но на момент изучения этой темы в школе разрешимая. Возможно и обратное: нестандартная на первый взгляд задача после ее переформулирования становится стандартной.

НЕСТАНДАРТНЫЕ ЗАДАЧИ В ОБУЧЕНИИ МАТЕМАТИКЕ

У учащихся необходимо формировать умение решать и стандартные, и нестандартные задачи,

Обучение учащихся решению стандартных задач показано ранее.

Решение нестандартной задачи — процесс творческий. Как он осуществляется реально, каково соотношение в нем интуитивного и логического, уследить практически невозможно. Однако очевидно, что и для логики, и для интуиции, проявляющихся в решении задач, необходимо создавать базу.

Базовые компоненты умения решать задачи можно разделить на общелогические и специфические. Охарактеризуем их более подробно.

Если проанализировать процесс решения задач из различных разделов математики и даже из различных предметных областей, то можно oбнаружить, что в нем проявляются одни и те же умения.

Решающий задачу должен уметь:

• распознавать объекты;

• выделять условие, его элементы и требование задачи и его элементы;

• конструировать графические, символические, схематические и т. п. модели содержания задачи;

• переводить содержание задачи на язык определенной теории;

• выводить следствия из элементов условия (заменять термин определением понятия, переходить от понятия к его свойствам);

• переосмысливать объекты в плане других понятий;

• преобразовывать требование задачи в равносильное ему;

• переходить от понятия к его признаку и от признака к понятию;

• интерпретировать символические записи;

•соотносить с условием и требованием задачи сбои мыслительные действия с чертежом;

• видеть различные пути решения задачи;

• формулироватьпроизводные задачи и т. д.

Такой достав общелогических умений обоснован в монографии Г И. Саранцева [37, с. 43-53].

К общелогическим также можно отнести умение

• строить цепочки умозаключении методом синтеза;

• строить цепочки умозаключений методом анализа;

• обнаруживать ситуации, в которых применимы некоторые специиальные методы решения (доказательство приведением примера, методом от противного, методом математической индукции и т. д.); применять эти методы.

Наряду с общелогическими существуют и специфические умения —умения, характерные для той или иной темы, для того или иного понятия, отношения или действия.

Рассмотрим, например, умение сравнивать два числа. В V-VI классах вводятся правила сравнения натуральных чисел, десятичных дробей, обыкновенных дробей, чисел, среди которых есть отрицательные. В VI классе положительные числа сравниваются нахождением их частного. В VIII" классе формулируются общие определения "число а больше (меньше) числа b". После введения иррациональных чисел появляется возможность сравнения неотрицательных чисел посредством сравнения их квадратов.

Если в конце,VIII класса ученик получил задание сравнить числа и 2,7, то он может действовать в соответствии со следующим правилом: "Чтобы сравнить два положительных числа, можно попытаться а) найти разность этих чисел и определить ее знак; б) найти частное этих чисел и сравнить его с единицей; в) сравнить квадраты этих чисел". Пункты б) и в) оказываются продуктивными, т. е. с их помощью нахо­дятся два способа решения задачи. Сформулированное здесь правило принято называть эвристическим правилом или эвристикой.

Вообще эвристика — это наука, исследующая закономерности творческой деятельности человека и разрабатывающая пути управления эвристическими процессами [33, с. 5}. Проблемой эвристики занимают­ся такие известные психологи, как В. Н. Пушкин, Ю.;Н. Кулюткин, проблемой педагогической эвристики — В. Н. Соколов [40].

В то же время эвристикой можно считать такой прием, который человек сформировал у себя в ходе решения одних задач и более или менее сознательно переносит его на другие задачи [33, с 21] С таким пониманием эвристик мы встречаемся в работах Д. Пойа, Л. М. Фридмана и др. Понятие "эвристическое правило" здесь, может быть, подходит больше. В. Н. Соколов трактует его следующим образом: "Эвристическое правило — элементарная единица методологических средств, содержащая рекомендации к выбору возможного действия в условиях альтернативного поиска" [40, с. 237].

Каждая тема школьного курса математики дает свой набор эвристических правил, которые используются в дальнейшем при поиске решений задач методом анализа или синтеза.

Например, в теме "Подобные треугольники" целесообразно выделить такие эвристики:

Чтобы найти отношение (доказать пропорциональность) отрезков,

можно

• заменить отношение отрезков отношением площадей треугольников;

• рассмотреть треугольники, сторонами которых служат эти отрезки, доказать их подобие;

• рассмотреть отрезки, высеченные параллельными прямыми на двух других прямых.

Здесь сформулированы эвристические правила, связанные с признаками понятий и отношений, они направлены на формирование действия подведения под понятие и применяются при поиске решения задачи ,методом анализа.

Можно сформулировать эвристики в форме, позволяющей использовать их в процессе поиска решения задачи методом синтеза. Они связаны со свойствами понятий и отношений и направлены на действие выведения следствий. Приведем примеры таких правил.

Если	Можно пытаться использовать
1)даны два подобных треугольника	а) равенство соответственных углов этих треугольников б) пропорциональность сходственных сторон;
2)дан угол, стороны которого пересечены параллельными прямыми	а) подобие треугольников; б) пропорциональность отрезков, отсеченных на сторонах угла;
3)в прямоугольном треугольнике проведена высота к гипотенузе	а) подобие треугольников; б) высоту как среднюю пропорциональную величину; в) каждый катет как среднюю пропорциональную величину

Многие и общелогические, и специфические умения, входящие, в деятельность по решению задачи, формируются у учащихся в ходе реализации технологий усвоения определений, правил, теорем на этапах подготовки к восприятию, восприятия и осознания, осмысления. Но в большей степени это происходит в процессе специальной работы над задачей под руководством учителя.

Если учитель ставит цель не просто получить ответ задачи, но и учить чему-то при ее решении, то задача выступает здесь как самостоятельная дидактическая единица. Разные авторы называют ее по-разному: учебная, познавательная, ключевая задача. При этом разли­чают задачу-факт и задачу-метод [45]. Если в результате решения задачи устанавливается новый факт, формула, свойство или признак какого-либо понятия или отношения, то имеем задачу-факт, или задачу-теорему. Если в процессе решения задачи обнаруживается какой-либо новый для учащихся метод, способ, прием рассуждений, решения или составления задачи, то имеем задачу-метод. Есть учебные задачи, кото­рые одновременно иллюстрируют что-то новое в решении и дают интересный и важный результат. На одной задаче можно иллюстрировать не один прием или метод. Для разных приемов могут быть использованы разные задачи. Так что число и содержание ключевых задач в теме определяется неоднозначно. Много здесь зависит от темы, от мастерства учителя, от целей, которые он ставит, и от особенностей класса.

Примеры ключевых задач

1. Решить уравнение (В теме "Основное свойство пропорции",VI класс).

2. Функция задана формулой у=-Зх+5.

а)Найти у(-2), у(0), у(1);

б) Найти значение х, при котором значение у равно -1. (В теме "Функция". VIIкласс).

3. Доказать, что а² +b² > 2аb, если а≠ b. (В теме "Числовые неравен­ства", VIII класс).

4. Доказать, что если а> b, то b <а. (Там же).

5. Дан параллелограмм ABCD и точка М, симметричная точке D от­носительно точки С. Доказать, что площадь параллелограмма ABCD и площадь треугольника AMD равны. (В теме "Площадь многоугольника", VIII класс).

6. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Доказать, что площадь четырехугольника равна половине, произведения диагоналей. (Там же).

Задачи 4 и 6 — это задачи-факты, 1, 2, 3, 5 — задачи-методы.

Ключевые задачи по теме выявляются на основе анализа всех задач, предлагающихся в учебнике, а также максимально возможного числа задач из других источников. Основные параметры анализа задачного материала приведены в п. 3.1 настоящего пособия.

В учебниках алгебры ключевые задачи, как правило, перечислены и решены в текстах соответствующих разделов. В учебниках геометрии многие задачи-факты приведены среди других задач, но даны с реше­ниями, а задачи-методы никак не выделены.

Ключевая задача — это самостоятельная дидактическая единица, единица усвоения. Но предметом усвоения здесь является не сама задача, а либо ее результат, либо общий метод рассуждений, способ реше­ния, либо отдельный прием, использованный в решении, либо прием составления, основанный на этой задаче, и т. д. Фактически предметом усвоения являются умения, познавательные средства, связанные с решением задач. Поэтому в процессе работы над ключевой задачей с учащи­мися важно на этапах поиска решения и анализа решения выделить те элементы, из-за которых задача выбрана в качестве ключевой.

Поиск решения либо показывает сам учитель, либо он осуществляется в диалоге учитель-ученик, либо в условиях фронтальной работы под руководством учителя.

После завершения этапа решения делаются выводы по задаче.

Если решалась задача-факт, то этот факт каким-то образом фиксиру­ется (в сводке формул, в таблице, в тетради по теории или другим спо­собом), учитель может пояснить учащимся, что в дальнейшем этот факт можно считать установленным и использовать его как известный. Таковы, например, формула площади ромба, выраженная через диагонали, свойство биссектрисы внутреннего угла треугольника, соотношение между средним арифметическим и средним геометрическим двух положительных чисел, формула корней квадратного уравнения с четным вторым коэффициентом и многие-многие другие.

Если при решении задачи применялся какой-то новый прием поиска решения или составления задачи, то этот прием также выделяется и выясняются возможности его применения, ситуации, в которых можно пытаться его применить. Например, это схемы поиска решения методом синтеза, анализа (восходящего и нисходящего), варианты переформулирования задачи, схемы решения задач тем или иным методом, специфи­ческие приемы, вытекающие из конкретных тем, и т. д.

Если рассматривались различные способы решения одной задачи, то выясняется, откуда появились эти различные способы, что наводит на мысль о возможности других способов решения.

Если на основе одной задачи составляются новые задачи, цепочки взаимосвязанных задач, то опять-таки нужно сделать выводы о том, как, на каком основании, из каких соображений возникла мысль о получении новых задач и как новые задачи появились (процесс их составления).

Основы проектирования технологии работы с текстовой (сюжетной) задачей на каждом этапе рассмотрены в п. 2.5 пособия.

Проиллюстрируем технологию работы с различными ключевыми задачами, представляющими собою элементы системы задач по теме. В качестве примера выберем тему "Параллельные прямые" (VII класс).

Логико-математический анализ теоретического и заданного материала с позиций развивающего обучения показывает, что в теме "Параллельные прямые" достаточно выделить три ключевые задачи (п. 3.1). Характеристику этих задач как ключевых и технологию работы с ними на этапах поиска решения и анализа решения и будем рассмат­ривать.

Задача I. Доказать, что если при пересечении двух прямых а и b секущей накрест лежащие углы не равны, то прямые а и b пересекаются. Покажем сначала вариант оформления решения (рис. 10).

Д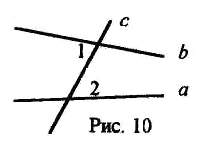 ано: а, b — прямые, с — се­кущая,

1, 2- накрест лежащие,

1≠ 2 .

Доказать: а и b пересекаются.

Решение:

1. Две прямые на плоскости либо пересекаются, либо параллельны. Докажем, что прямые а и b не параллельны.

2. а) Предположим, что прямые а и b параллельны.

б) Тогда 1 = 2 по свойству параллельных прямых накрест лежащих углах,

в) 1 = 2-противоречие с условием,

г)Значит, предположение о параллельности прямых а и b неверно. Следовательно, прямые а и b не параллельны, т. е. пересекаются. Объясним, почему задача выбрана в качестве ключевой. Во-первых, в теоретической части темы доказаны теорема-признак параллельности прямых по накрест лежащим углам и обратная ей соответствующее свойство. В задаче сформулирована третья теорема из логического квадрата - теорема, противоположная исходной. Хотя термин можно и не вводить, важно, чтобы учащиеся повстречались с такой теоремой и методом ее доказательства.

Во-вторых, задача необычная по формулировке. Чаще всего требуется доказывать параллельность прямых. Считается, что вывод о непараллельности прямых можно сделать автоматически, и учащиеся часто делают это, ссылаясь на признак параллельности, но не на свойство,

В-третьих, решением задачи доказывается признак пересечения прямых.

В-четвертых, при решении задачи применяется метод от противного, основательное знакомство с которым происходит именно в теме о параллельных прямых. В данной задаче он хорошо прослеживается (см. пункты 2, а-г) и есть возможность выявить одну из характерных ситуа­ций, в которых этот метод применим.

После создания графической и символической модели содержания задачи нужно дать возможность порассуждать учащимся (без каких-либо записей), поскольку теоретически для решения такой задачи все подготовлено. Для оказания помощи в поиске решения можно предло­жить следующую систему вопросов и (или) фрагментов рассуждений:

• Как могут располагаться две прямые на плоскости?

• "Две прямые на плоскости параллельны". Как высказать то же самое, но другими словами? ("не пересекаются").

• Как иначе сказать: "Две прямые на плоскости пересекаются?" ("непараллельны").

• Как же тогда можно сформулировать требование задачи?

• В тех случаях, когда в требовании задачи или теоремы есть отрицание "не", при доказательстве используется метод от противного. Примените его здесь (считаем, что схема доказательства методом от противного учащимся знакома, в классе может быть вывешен соответствующий плакат).

Далее учитель или способный на это ученик показывает образец рассуждений и оформление решения задачи.

В порядке анализа решения можно предложить учащимся следующие вопросы и задания:

• Что требовалось доказать в задаче?

• А мы что доказали?

• Какой метод доказательства был использован?

•Что "навело" на этот метод? (Наличие в требовании отрицания "не").

• Каков теоретический базис доказательства? Или: Какие определения, теоремы, аксиомы были использованы при решении задачи?

• При изучении темы мы доказали признаки и свойства параллельности прямых. А что мы доказали сейчас? (Признак пересекающихся прямых).

• Какие еще признаки пересекающихся прямых можно попытаться

доказать?

После такой беседы делаем следующие выводы:

1. Требование задачи можно переформулировать и тогда становится видно, какой метод нужно применить.

2. Если в требований задачи или теоремы есть отрицание "не", то можно попытаться применить метод от противного.

3.Доказан признак пересекающихся (признак непараллельности) прямых. Сформулируем его.

4. Можно доказать и другие признаки пересекающихся прямых. При этом использовать метод от противного и соответствующее свойство параллельных прямых (очевидно, что этот способ доказательства не единственный).

Задача 2. По данным рис. 11 найти 1.

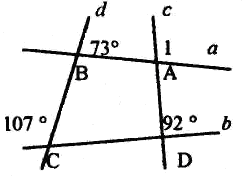
Задача выбрана в качестве ключевой по ряду показателей.

Во-первых, при ее решении используются и признаки, и свойства параллельности прямых, т е возможно их противопоставление.

Во-вторых, выбор признаков здесь не однозначен.

В-третьих, не ясно, параллельность каких прямых нужно доказывать. На рисунке в учебнике есть подсказка: две прямые изображены параллельными. Как правило, учащиеся и доказывают параллельность этих прямых, оставляя без внимания две другие. Однако, если мы стремимся приучать школьников к полноте аргументации, здесь есть хороший по­вод для этого.

В-четвертых, на задаче хорошо иллюстрируется поиск ее решения аналитико-синтетическим методом.

Система вопросов (если в ней будет необходимость) должна вывести учащихся на следующие рассуждения: угол 1 и угол в 73° — соответственные при прямых с и d и секущей а, угол 1 и угол в 92° — соответственные при прямых а и b и секущей с. Поэтому хорошо бы выяснить, как взаимно расположены прямые а и b и прямые c u d. Поскольку угол 1 образован прямыми а и с, то в качестве секущих для выяснения параллельности можно использовать прямые b и d Таким образом, рассмотрим прямые а и b и секущую d, затем — прямые с и d и секущую b.

Дальнейшие рассуждения очевидны.

Возможная система вопросов:

•С какими известными углами и как взаимосвязан угол 1?

• При каком же условии можно будет найти угол 1? (Если среди прямых есть параллельные.)

• Параллельность каких прямых можно пытаться доказать? (a и b, с u d.)

• Что для этого можно использовать? (Признаки параллельности прямых.)

• Какую же секущую для прямых а и b будем рассматривать? А для прямых с и d?

В ходе дальнейших рассуждений (синтез) выясняем, что по признаку параллельности прямых прямые а и b параллельны, а по признаку пересекающихся прямых прямые с и d пересекаются. Тогда 1 = 92° по свойству параллельных прямых о соответственных углах и свойству равных углов (если углы равны, то их градусные меры равны).

После оформления решения проводится его анализ. Можно предложить вопросы:

• Каков теоретический базис решения данной задачи?

• Какие признаки и для чего были использованы?

• Какие свойства и для чего были использованы?

• Можно ли было использовать другие признаки параллельности прямых?

• Можно ли было использовать другие свойства параллельных прямых? (Можно, но решение было бы длиннее, а это нерационально.)

Выводы по решению задачи

1. Для нахождения величины угла можно использовать связь между углами, образованными при пересечении двух параллельных прямых третьей, т. е. свойства параллельных прямых.

2. Параллельность прямых устанавливается с помощью признаков параллельности. При этом могут быть использованы разные признаки.

3. Поиск решения задачи можно вести начиная с требования. В данной задаче краткая схема будет такой: чтобы найти угол 1, нужно установить взаимное расположение прямых а и b, c и d. Для этого используются признаки параллельных, и пересекающихся прямых. Чтобы их использовать, нужно найти величины накрест лежащих, соответственных или односторонних углов при пересечении двух прямых секущей.

4. Несмотря на то, что при решении задачи мы сразу "вышли" на параллельные прямые а и Ь, взаимное расположение прямых с и d тоже пришлось устанавливать. Если бы вдруг они тоже оказались параллельными, то угол 1 был бы равен и 73 °, и 92°, а это; невозможно.

Задача 3. Отрезок ВК — биссектриса треугольника ABC Через точку К проведена прямая, пересекающая сторону ВС в точке М так, что ВМ = МК. Доказать, что КМ и АВ параллельны.

Покажем графико-символическую модель содержания задачи (рис. 12).

Д ано: А АВС,

1. ВК — биссектриса,

2. М ВС, ВМ = МК.

Доказать: КМ || АВ.

Почему задача отнесена к ключевым?

Во-первых, прямые и секущая здесь не заданы непосредственно. Их нужно выделять среди других заданных фигур, переосмысливать заданные фигуры в плане других понятий (биссектриса ВК — часть секущей для прямой КМ и прямой, которая задана отрезком АВ — стороной треугольника, часть прямой КМ, отрезок КМ — сторона треугольника ВКМ, накрест лежащие углы, из равенства которых последует парал­лельность прямых, являются углами треугольников).

Во-вторых, заключение о равенстве углов АВК и ВКМ требует довольно длительных промежуточных рассуждений: замена термина определением биссектрисы, выведение следствия на основе определения, установление вида треугольника ВКМ на основе определения, выведение следствия на основе свойства равнобедренного треугольника, сопос­тавление равенств и выведение нужного.

В-третьих, на решении этой задачи хорошо прослеживается синтез и именно этот способ рассуждений нужно показать учащимся.

Всем перечисленным здесь мыслительным операциям, действиям, способам рассуждений мы обучаем учащихся при решении этой задачи, формируем у них соответствующие умения.

Как работать с данной задачей в процессе поиска решения и какие сделать выводы по завершении решения — установить нетрудно. Поэтому на перечисленных здесь этапах мы останавливаться не будем.

Есть еще один аспект, благодаря которому задачу можно рассматривать как ключевую: на основе данной задачи можно составить две новых. В главе о параллельных прямых впервые явно вводятся понятие теоремы, обратной данной, и способ ее получения. В порядке закрепления этих понятий предлагаем учащимся сформулировать предложение, обратное данной задаче. Однако при этом выясняется, что задача сложная, поскольку ее условие состоит из двух элементов (на символической модели они занумерованы). Объясняем, что каждый из элементов условия можно поменять с требованием. Тогда получаются две новых задачи. Для них сначала составляются следующие символические модели

(рис. 12).

Задача 3.1. Задача 3.2.

Дано: Δ ABC, Дано: Δ ABC,

ВК — биссектриса, К АС, М ВС, КМ || АВ,

КМ || АВ, M ВС. ВМ = МК.

Доказать: ВМ = МК. Доказать: ВК — биссектриса.

Теперь по символическим моделям можно составить тексты и ре­шить задачи.

Выводы после этой части работы

1. На основе одной задачи можно составить новую задачу, обратную данной. Для этого условие и заключение нужно поменять местами.

2. Если условие задачи состоит из двух элементов, а требование из одного, то каждый элемент условия можно поменять с требованием. Следовательно, для такой задачи можно составить две обратных.

Итак, в теме выбраны всего три ключевые задачи. Однако специальным образом организованная работа над ними позволяет зафиксировать внимание учащихся на самых разных общелогических и специфических действиях, входящих в деятельность по решению задач. Эти действия, выделены выше при рассмотрений причин, по которым задачи выбраны в качестве ключевых, и в выводах по решению задач.

Таким образом, уровень развития учащихся проявляется, в частности, и в том, какие задачи и как они решают самостоятельно. Количество решенных задач автоматически переходит в качество — умение решать задачи — лишь у незначительной части учащихся. В большинстве же случаев для формирования умений решать задачи нужна целена­правленная работа учителя.

Умственную деятельность по решению задач составляют общелогические и специфические действия. Умения выполнять эти действия и необходимо формировать у школьников. Существенную роль в решении этой проблемы играют ключевые задачи, их отбор и специальная работа над ними.