10. Теоремы Муавра-Лапласа

Пусть в каждом из независимых испытаний событие A может произойти с вероятностью , (условия схемы Бернулли). Обозначим как и раньше, через вероятность ровно появлений события А в испытаниях. кроме того, пусть – вероятность того, что число появлений события А находится между и .

Локальная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

где - функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Интегральная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2)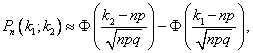 где - функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:

а)

б) при больших верно .

Теоремы Лапласа дают удовлетворительное приближение при . Причем чем ближе значения к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).

Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Решение. По условию , откуда

По таблицам найдем .

Искомая вероятность равна:

Пример. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:

В – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20

Решение. Изготовление детали – это испытание, в котором может появиться событие А – изделие бракованное – с вероятностью . Находим . Можно применять формулы Лапласа:

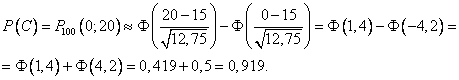
Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.

Пример. Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы c вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?

Решение. Будем считать, что событие произошло, если турист пообедал у заинтересованного владельца. По условию задачи , . Нас интересует такое наименьшее число посетителей , что вероятность одновременного прихода не менее чем туристов из числа с вероятностью успеха приблизительно равна вероятности переполнения ресторана, т.е. .

Таким образом, нас интересует такое наименьшее число , что . Применим интегральную теорему Муавра-Лапласа.

В нашем случае: ­– неизвестно, , , . Тогда

Используя таблицы для функции , находим, , и, значит, . Следовательно, в ресторане должно быть 62 места.

11. Геометрическая вероятность

Определение геометрической вероятности используется в задачах, когда общее и благоприятное число исходов бесконечно.

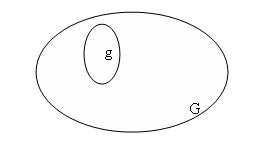
Бросается наудачу точка в область G. Найти вероятность того, что точка попадет в область g (множество g с квадрируемой границей).

Вероятность в этом случае будет вычисляться по формуле

p=mes(g)mes(G)

Задача. Два студента условились встретиться в определенном месте между 12-ю и 13-ю часами. Пришедший первым ждет другого не больше 20 минут, после чего уходит. Найти вероятность того, что встреча произойдет.

Решение.

Пусть x - момент времени прихода первого студента

Пусть y - момент времени прихода второго студента

x, y ∈ [0;60] (определение того, что встреча произойдет между 12 и 13 часами, то есть в промежуток времени в 60 минут) - задает область G.

∣ x-y∣≤ 20 (определение того, что студент пришедший первым ждет второго не больше 20 минут) - задает область g.

Тогда области, задаваемые неравенствами, будут выглядеть следующим образом.

Тогда вероятность будет считаться как отношение площадей двух областей g и G. p(A)=60*6060*60−40*40=94

Классическое определение вероятности случайного события предполагает конечное число всех исходов испытания. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно. В этом случае, если позволяют обстоятельства, используют понятие геометрической вероятности.

Геометрической вероятностью события A называется отношение меры области, благоприятствующей появлению события , к мере всей области исходов

Задача бюффона.    На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии . На плоскость наудачу брошена игла длины . Какова вероятность того, что игла пересечет одну из прямых?

Решение.   Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга.

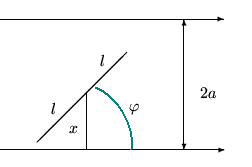
Обозначим через расстояние от середины иглы до ближайшей прямой, а через  —  угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника .

Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: .

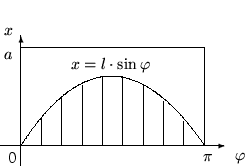
Площадь области , точки которой удовлетворяют такому неравенству, равна

И так как , то искомая вероятность равна .

12.цепи маркова. Пусть { , , ..., } - множество состояний некоторой физической системы. В любой момент времени система может находиться в одном состоянии и меняет свое состояние только в моменты , , ..., , .... Для однородных цепей Маркова вероятность перехода системы из состояния в состояние за один шаг зависит только от того, из какого состояния в какое осуществлялся переход.

Вероятности перехода удобно располагать в виде матрицы. Обозначим ее

и будем называть матрицей перехода однородной цепи Маркова за один шаг. Матрица P обладает следующими свойствами:

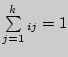а) б) ( = 1, 2, ..., ;

т.е. сумма элементов каждой строки матрицы перехода равна единице. Квадратные матрицы, для которых выполняются условия а) и б), называются стохастическими.

Вектор , где - вероятность появления состояния ( = 1, 2, ..., в начальном испытании, называется вектором начальных вероятностей.

Свойства однородных марковских цепей полностью определяются вектором начальных вероятностей и матрицей вероятностей перехода. В некоторых случаях вместо матрицы P используют ориентированный граф, вершинами которого являются состояния цепи, а стрелка, идущая от состояния в состояние с числом рядом с ней, показывает, что из состояния возможен переход в состояние с вероятностью . В том случае, когда 0, соответствующее ребро не проводится. В случае однородных цепей Маркова с вектором начальных вероятностей появляется еще начальная вершина графа, которая соединяется с состоянием ребром с числом рядом с ним.

Можно показать, что матрица перехода P за шагов находится как .

Если из состояния система может перейти в состояние с положительной вероятностью за конечное число шагов, то говорят, что достижимо из . Состояние называется существенным, если для каждого состояния , достижимого из достижимо из . В противном случае называется несущественным состоянием.

Понятие марковской цепи принадлежит русскому математику А.А. Маркову, чьи первые статьи по этому вопросу при решении лингвистических проблем были опубликованы в 1906-1908 гг.

Пример 51. Частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты , , , ...Частица может находиться в точках с целочисленными координатами 1, 2, 3, 4, 5; в точках 1 и 5 находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью и влево с вероятностью , если частицы не находятся у стенки. Если же частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка [1,5]. Найти матрицу перехода P и ей соответствующий граф.

Решение. Пусть , = 1, 2, 3, 4, 5. Тогда граф перехода выглядит следующим образом:

Рис. 33

а матрица перехода -

Пример 52. Вероятности перехода за один шаг в цепях Маркова задаются матрицей:

Требуется:

а) найти число состояний;

б) установить, сколько среди них существенных и несущественных;

в) построить граф, соответствующий матрице P.

Решение.

а) 4 состояния.

б) состояния , несущественны, поскольку остальные состояния достижимы из них, но недостижимо из , а недостижимо из ; состояния и являются существенными.

в)

Рис. 34

Пример 53 (задача о скрещивании). В близко родственном скрещивании две особи, и среди их прямых потомков случайным образом выбираются две особи разного пола. Они вновь скрещиваются, и процесс этот продолжается бесконечно. Каждый родительский ген может передаваться с вероятностью , и последовательные испытания независимые. Имея три генотипа AA, Aа, аа для каждого родителя, мы можем различать шесть комбинаций родителей, которые пометим следующим образом:

=AA AA, = AA Aа, = AA аа, = Aа Aа, = Aа аа, = аа аа. Найдите граф и матрицу перехода.

Решение. Рассмотрим, какое потомство и с какой вероятностью может быть у особей разного пола, если они выбираются из .

Пусть = { -й потомок}, = 1, 2 и , - разного пола, тогда варианты потомков и их вероятности можно найти по следующему графу:

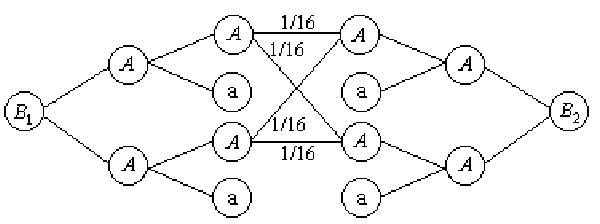
Рис. 35

Получаем, что

Аналогично, находим и вероятности других переходов:

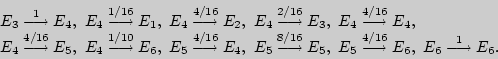
Тогда искомый граф перехода выглядит следующим образом:

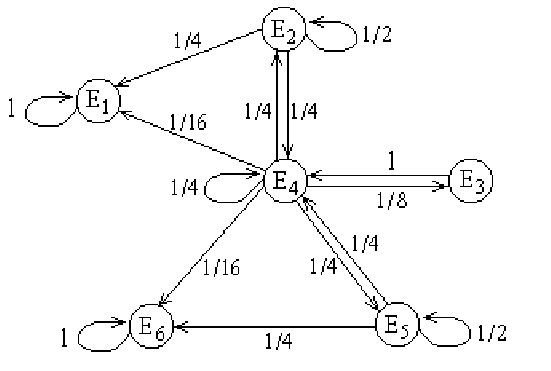
Рис. 36

а матрица перехода -