
- •1. Определяемые и неопределяемые понятия
- •3. Логические операции над высказываниями
- •6, Логическое следование. Логическая эквивалентность. Прямые, обратные и контрапозитивные утверждения. Необходимые и достаточные условия.
- •4. Формулы логики высказываний. Законы логики.
- •2, Если ų1 и ų2 – формулы логики высказывания, то отриц.Ų1,( ų1 ų2),( ų1 ų2) (ų1 ų2), (ų1 ų2) формулы логики высказываний.
- •5. Высказывательня форма. Кванторы.
- •7. Метод математической индукции
- •16. Перестановки
16. Перестановки
17. Перестановки с повторениями
Общая задача: сколько существует перестановок из n-предметов, различных типов по расположенных на n-различных местах.
Число эл. в каждой перестановке n=n1+n2+…nk
Если все эл.разные – n!
В данной перестановке эл.первой группы можно переставлять друг с другом n1! Способами, 2 группа – n2! Способами и т.д.
Перестановки элементов этих групп можно делить независимо друг от друга. Переставлять можно n1!*n2!*nk! Способами
Число
различных перестановок с повторениями
= Pn=
18. Размещения.
17. Перестановки с повторениями
Общая задача: сколько существует перестановок из n-предметов, различных типов по расположенных на n-различных местах.
Число эл. в каждой перестановке n=n1+n2+…nk
Если все эл.разные – n!
В данной перестановке эл.первой группы можно переставлять друг с другом n1! Способами, 2 группа – n2! Способами и т.д.
Перестановки элементов этих групп можно делить независимо друг от друга. Переставлять можно n1!*n2!*nk! Способами
Число различных перестановок с повторениями = Pn=
19. Размещения с повторениями.
Если
число видов =n,
а в каждое размещение входит k-элементов,
то можно составить
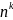 размещений с повторениями.
размещений с повторениями.

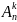 =n*
=n*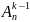 =n*
=n*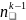 =
=
20. Сочетание
При выборе r объектов из n без учета порядка мы имеем дело с сочетаниями из n объектов по r.
Пусть имеется множество М, сост.из n различных эл. Всякое подмножество множества М, содерж. K эл. Называется сочетанием из данных n элементов по k элементов. Из определения следует, что 2 различных сочетания из данных n-элементов по k- элементов отлич.по меньшей мере одним элементом.
Чтобы
получить все размещения из элементов
по k
нужно в каждом сочетании из n
элементов по к произвести Рк
перестановок.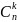 =
=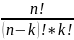
21.
Биномиальная формула Ньютона.
Используя формулу Ньютона можно
доказать, что для каждого действительного
числа большего 1 и любого натурального
n,
больше 1 имеет место неравенство Бернулли
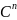 >1+n(c-1)
>1+n(c-1)
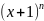 представляет собой
многочлен степени n,
коэффициенты которого совпадают с
элементами соответствующей строки
треугольника Паскаля.
представляет собой
многочлен степени n,
коэффициенты которого совпадают с
элементами соответствующей строки
треугольника Паскаля.
Поскольку
n
строка в тр. Паскаля имеет вид
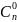 ,
,
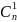 ,
,
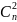 ,
,
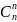 ,
то предполагается, что
это
+
х+
,
то предполагается, что
это
+
х+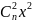 …
…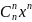
Это равенство обычно записывают в виде:
=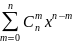
=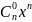 +
+ +…+
+…+
