9. Критерий Хотеллинга для двух многомерных выборок.

Сопоставляются параметры 2х выборок, причем объемы выборок могут быть разными:

- объединен. м-ца:

K₁ - центриров. м-ца по 1ой выборке

K₂ - центриров. м-ца по 2ой выборке

Найденная величина сравнивается с скорректированным кр. Фишера (табулированным значением):

Если , то мы считаем данные сов-ти схожими по их многомерным мат. ожиданиям.

Но наша проверка не всегда дает нужный результат, т.к. сравнивая векторы, мы никогда не узнаем по каким координатам наши вектора не совпали. Для этой цели испол-ся частный критерий Хотеллинга:

Вектор - сформированный многомерный вектор:

Ненулевые координаты свидетельствуют о том, что именно эти признаки мы хотим проверить.

Нулевые координаты соответствуют признакам, которые не нужно проверять.

Рассчитанная статистика также сравнивается с скорректированным Фишером:

- сколько признаков брали на проверку

10. Критерий Бартлетта и проверка гипотезы об однородности дисперсии.

Одновременное совпадение ковариац.-дисперсион. матрицы случайным быть не может.

Одномерный критерий Бартлетта:

– номер выборки, - объем выборки i

A – отношение, связывающее через коэффициенты все дисперсии (частные и совокупные)

, ,

С < 1 – коэффициент, связывающий степени свободы, если С < 1 - критерий не работает

Если ( зависит только от количества взятых выборок,  = l - 1), то гипотеза Н₀ принимается, следовательно, дисперсия однородна. В противном случае гипотеза Н₀ отвергается и мы трактуем несхожесть совокупностей по дисперсиям.

Многомерный критерий Бартлетта:

Выводится из одномерного критерия вручную.

n_i – объем i-й выборки

h_i = n_i – 1 – скорректированный объем на одну степень свободы

h – общий коэффициент

K_i – матрица центрированных значений для многомерной выборочной величины X_i

А – связывает все многомерные ковариационно-дисперсионные матрицы

C – получен экспериментальным путем, если С < 1, то все рассчитано правильно, а если С < 1 - критерий не работает, т.к. объем недостаточен выборок.

Если , то гипотеза Н₀ принимается.

11. Груб. Ошибки. Причины их появл-ия в статистич. Сов-ти. Методы их выявл-ия.

Два типа данных, засоряющих статистическую совокупность:

1. Данные, не существенно отличающиеся от значений, наиболее часто встречающихся в изуч. сов-ти.

2. Резко выделяющиеся данные – грубые ошибки (выбросы)

Следствием данных, засоряющих статистическую совокупность, является сильное искажение параметров, что дает неверные рез-ты оценивания. Для таких данных существуют специал. методы обработки.

Причины появления грубых ошибок:

1. особ-ти отдел. элементов, сильно реагирующих на случ. фактор (как правило, это нормал. величины)

2. непрофессиональная обработка первичных данных (ошибки группировки, классификации) (с ошибками такого рода чаще всего встречаются экономисты)

3. ошибки при сборе, регистрации и наборе данных (ошибки оператора)

Два подходы выделения грубых ошибок:

1. устранение из совокупности грубых ошибок и оценка параметров по оставшимся данным

2. работа с каждой груб. ошибкой, т.е. получение истин. значений признака и оценку грубых значений

Методы распознавания грубых ошибок:

1. Метод Смирнова – Граббса (сначала ряд ранжируется)
Для утяжеленного левого хвоста: , - модифицир. знач-я ранжир. ряда , Если (табличное значение), то проверяемое значение оказалось грубой ошибкой.	Для утяжеленного правого хвоста: , - модиф. знач-я ранж. ряда Если , то проверяемое значение оказалось грубой ошибкой.
Минусы: - нечувствителен тогда, когда сильно засорена сов-ть или когда ГО концентрируются вокруг МО
2. Дисперсионный критерий Граббса (более точный, чувствительный) (сначала ряд ранжируется)
Для утяжеленного левого хвоста: , где - усеченная средняя снизу Если , то провер. знач-е - груб. ошибка	Для утяжеленного правого хвоста: , где - усеченная средняя сверху Если , то проверяемое знач-е – ГО
Связь с методом Смирнова – Граббса: и
3. L-критерий Титьена – Мура (используют для выявления нескольких грубых ошибок)
Для выявления одновременно k грубых ошибок в верхней части ранжированного ряда: ,	Для выявления одновременно k грубых ошибок в нижней части ранжированного ряда: ,
Если С(,n,k) > L, то k проверяемых значений оказались грубыми ошибками.
4. E-критерий Титьена – Мура (позволяет обнаруживать экстремальные значения как в правом, так и в левом хвосте распределения)

1) центрируем по модулю: ,

2) строится вариацион. ряд по абсолют. центриров. значениям: r₍₁₎ = maxd(x_i, ), …, r_(n) = mind(x_i, ),

где - расстояние от среднего значения

3) строится статистика для проверки гипотезы о том, что k наибольших по модулю наблюдений из модифицир. ряда оказались грубыми ошибками: ,

Если , то k проверяемых значений оказались грубыми ошибками.
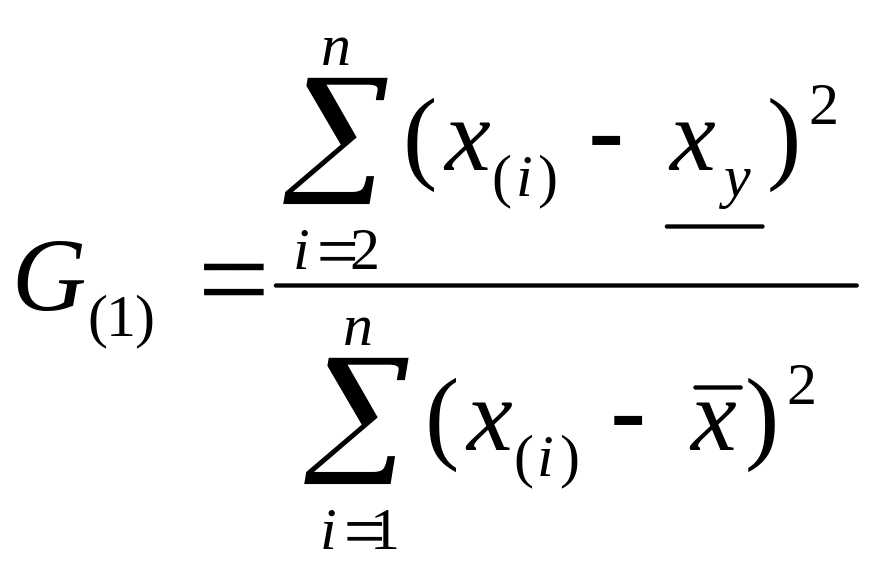