3. Приклад виконання практичних робот.

3.1 Завдання 1

Знайти наближене значення визначеного інтеграла методом трапеції і Симпсона. Оцінить погрішність наближених значень визначеного інтеграла. Обчислить уточнені по Річардсону наближені значення.

1. Розіб'ємо інтервал інтеграції на 6 частин з кроком h=0.1. Значення функції у вузлах розбиття занесемо в таблицю:

	0.2	0.3	0.4	0.5	0.6	0.7	0.8
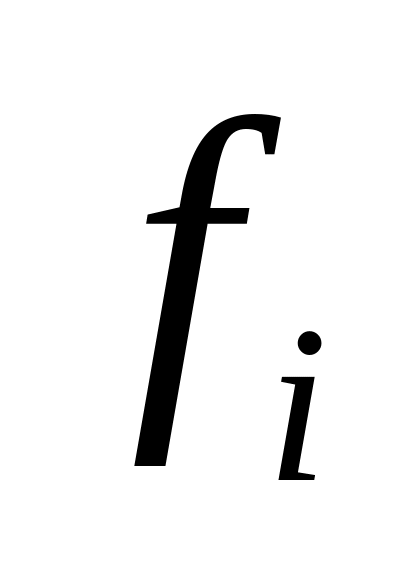
	0,3766	0.3668	0.3658	0.3747	0.3938	0.4228	0.4602

Обчислимо наближені значення з кроком h=0.1

а) Метод трапеції:

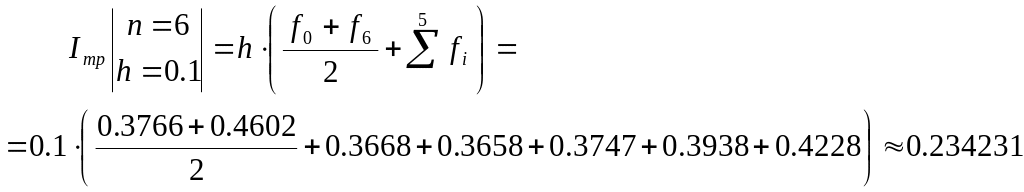
б) Метод Симпсона:

2. Розіб'ємо інтервал інтеграції на 12 частин з кроком h=0.05. Значення функції у вузлах розбиття занесемо в таблицю:

	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65	0.7	0.75	0.8
	0.3766	0.3707	0.3668	0.3651	0.3658	0.369	0.3747	0.383	0.3938	0.4071	0.4228	0.4406	0.4602

Обчислимо наближені значення з половинним кроком:

а) Метод трапеции:

б) Метод Симпсона:

3. Оцінимо погрішність наближених значень визначеного інтеграла, обчисленого з половинним кроком:

4. Обчислимо уточнені по Річардсону наближені значення

3.2 Завдання 2

Знайти точку локального мінімуму для функції с точністю на відрізку , по-перше відділив відрізки унімодальності. Для першего відрізка застосовувати метод «золотого перетину», для другого– метод діхотомії

Проведемо відділення точок локального мінімуму для функції на відрізку при і .

Обчислимо крок . Розіб'ємо відрізок точками , де

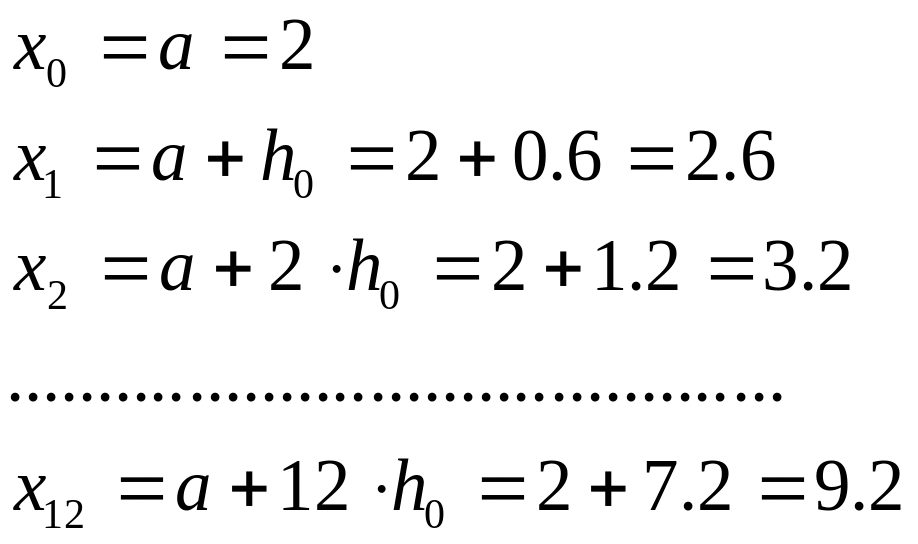
Обчислимо значення функції в отриманих точках і занесемо в таблицю 1.

Таблица 1

	0	1	2	3	4	5	6
	2	2.6	3.2	3.8	4.4	5.0	5.6
	-4.808626	-5.830948	-4.816351	-2.119265	1.318142	4.295084	5.771629
	7	8	9	10	11	12
	6.2	6.8	7.4	8	8.6	9.2
	5.231979	2.864647	-0.503388	-3.695575	-5.593792	-5.542888

Розглядаємо відрізки , , . Виберемо ті з них, для яких значення в середині відрізка не більш значень функцій на кінцях відрізка.

Наприклад, для відрізка :

Таких відрізків отримаємо два: з центром в точці і з центром в точці . На рисунку 1 ці відрізки виділені. Значить .

Проведемо ту ж процедуру з кроком . Результати обчислень занесемо в таблицю 2.

В даному випадку отримано також два відрізки: з центром в точці і з центром в точці . Число відрізків унімодальності .

Оскільки , то закінчуємо процес відділення. Отже, отримано два відрізки унімодальності і .

Таблиця 2.

0	2	-4.808626	12	5.6	5.771629
1	2.3	-5,568496	13	5.9	5.759022
2	2,6	-5.830948	14	6.2	5,231979
3	2,9	-5.572539	15	6.5	4.237578
4	3.2	-4.816351	16	6.8	2.864647
5	3,5	-3.629934	17	7.1	1,235826
6	3,8	-2.119265	18	7.4	-0.503388
7	4,1	-0.419288	19	7.7	-2.197635
8	4,4	1.318142	20	8.0	-3.695575
9	4,7	2.937826	21	8.3	-4.8634
10	5	4.295084	22	8.6	-5.596792
11	5,3	5.268674	23	8.9	-5.830239
			24	9.2	-5.542888

2. З точністю знайти точку локального мінімуму функції на відрізку унімодальності методом діхотомії

;

Розділимо початковий відрізок на чотири частини точками , , , , .

Обчислимо значення даної функції в цих точках і занесемо їх в таблицю 3:

Таблиця 3

	0	1	2	3	4
	8,6	8,75	8,9	9,05	9,2
	-5,597	-5,778	-5,83	-5,751	-5,542

Значення є найменшим, на наступному кроці розглядаємо відрізок . Його довжина рівна більше . Тому процедуру повторюємо. Обчислимо

Розділимо відрізок на чотири частини точками .

Значення і занесемо в таблицю 4:

Таблиця 4

	0	1	2	3	4
	8,6	8,75	8,9	9,05	9,2
	-5,597	-5,778	-5,83	-5,751	-5,542

є найменшим значенням, тому новий відрізок . Оскільки його довжина менше , то як точка мінімуму вибираємо , мінімальне значення - 5,83.

3. Знайти точку локального мінімуму функції на відрізку унімодальності з точністю методом золотого перетину.

1. Відрізок ділимо на три частини точками

Обчислимо значення функції в точках і

;

Оскільки , то ,

. Оскільки , то процес дроблення продовжується

2. .

Обчислимо . Оскільки , то

; ; ; ; .

3. .

Обчислимо . Оскільки , то

; ; ; ;

4. .

Обчислимо . Оскільки , то

; ; ; ; .

5. .

Обчислимо . Оскільки , то

; ; ; ; .

Обчислимо .

6. Довжина відрізка рівна , вона менше , тому дроблення відрізків завершено.

Точка локального мінімуму .

Значення функції в цій точці .

Обчислення занесемо в таблицю 5.

Таблиця 5

0	2,3	2,5293	-5,8159	2,6707	-5,8169	2,9
1	2,5293	2,6707	-5,8169	2,7585	-5,7588	2,9
2	2,5293	2,6172	-5,8302	2,6707	-5,7169	2,7586
3	2,593	2,5828	-5,8300	2,6172	-5,8302	2,6707
4	2,5828	2,6172	-5,8302	2,6363	-5,8274	2,6707
5	2,5828	2,6019	-5,8310	2,6172	-5,8302	2,6363
6	=2,60955			=-5,83075