
- •1. Екзаменаційні питання з дисципліни
- •(3 Модуль)
- •Завдання к практичним роботам
- •2.1 Варіанти к завданню №1
- •2.2 Варіанти к завданню №2
- •2.3 Варіанти к завданню №3
- •3. Приклад виконання практичних робот.
- •3.1 Завдання 1
- •3.2 Завдання 2
- •3.3 Завдання 3
- •8. Список літератури
- •До виконання контрольної роботи та типового розрахунку з дисципліни “Обчислювальна математика і програмування” для студентів денної і заочної форм навчання за спеціальностями:
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ВОЛОДИМИРА ДАЛЯ
СЄВЄРОДОНЕЦЬКИЙ ТЕХНОЛОГІЧНИЙ ІНСТИТУТ
ДМИТРІЄНКО Г.М.
Умови індівідуальних завдань
до практичних робот з дисципліни
(3 модуль)
“Обчислювальна математика і програмування”
для студентів денної і заочної форм навчання за спеціальностями:
7.091601 “Хімічна технологія органічних речовин”
7.091602 “Хімічна технологія неорганічних речовин”
7.091604 “Хімічна технологія палива і вуглецевих матеріалів”
7.091612 “Технологія переробки полімерів”
ЗАТВЕРДЖЕНО
на засіданні кафедри
вищої та прикладної математики
Протокол № 3 від 30.10. 2006р.
Сєвєродонецьк 2007
1. Екзаменаційні питання з дисципліни
“Обчислювальна математика і програмування”
(3 Модуль)
Вывод коэффициентов Котеса
Формула прямоугольников для приближенного вычисления определенного интеграла
Формула трапеции
Формула Симпсона
Правило Рунге для оценки погрешности приближенного значения интеграла
Использование МаthCad для приближенного вычисления определенного интеграла
Постановка задачи одномерной минимизации. Метод дихотомии
Метод отделения отрезков унимодальности
Метод “золотого” сечения
Постановка задачи многомерной минимизации. Метод градиентного спуска с дроблением шага
Метод градиентного спуска с постоянным шагом
Метод наискорейшего градиентного спуска
Использование МаthCad для решения задач одномерной и многомерной минимизации
Постановка задачи линейного программирования
Геометрический метод решения
Приведение системы ограничений к стандартному виду
Построение нулевого базисного решения. Критерий оптимальности
Алгоритм симплексного метода
Построение симплекс-таблиц
Использование МаthCad для решения задач линейного программирования
Завдання к практичним роботам
Знайти наближене значення визначеного інтеграла методом трапеції і Симпсона. Оцінить погрішність наближених значень визначеного інтеграла. Обчислить уточнені по Річардсону наближені значення.
Знайти точку локального мінімуму для функції
 с
точністю
с
точністю
 на
відрізку
на
відрізку
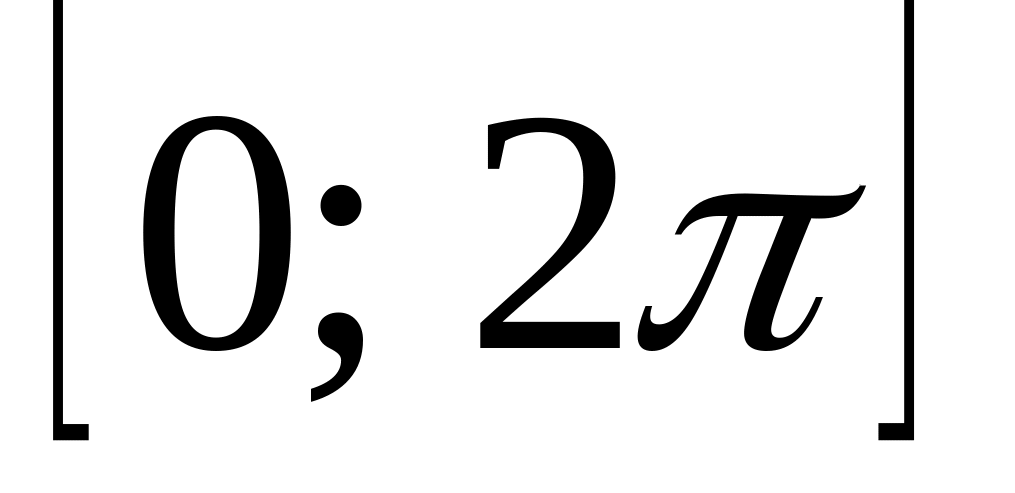 ,
предварительно відділив
відрізки
унімодальності.
Для парних
номеров варантів
для одного з відрізків унімодальності
застосовувати
метод «золотого
перетину»,
для не парних
номеров варантів
метод дихотомії
( n=10,
p=2)
,
предварительно відділив
відрізки
унімодальності.
Для парних
номеров варантів
для одного з відрізків унімодальності
застосовувати
метод «золотого
перетину»,
для не парних
номеров варантів
метод дихотомії
( n=10,
p=2)Знайти точку мінімуму і мінімальне значення цільової функції
 ,використовуючи метод градієнтного
спуску з дробленням кроку, с точністю
,використовуючи метод градієнтного
спуску з дробленням кроку, с точністю
 .
Точка початкового спуска
.
Точка початкового спуска
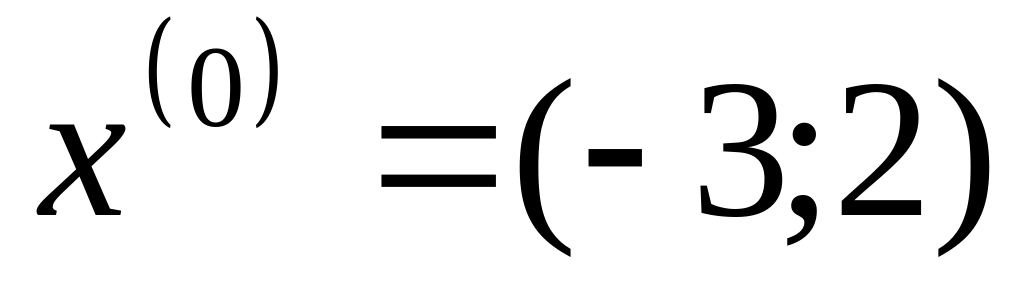 .
Крок
.
Крок
 .
.
2.1 Варіанти к завданню №1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.2 Варіанти к завданню №2
№ |
K |
n |
L |
m |
№ |
K |
n |
L |
m |
1 |
5 |
1 |
3 |
3 |
16 |
2 |
2 |
4 |
3 |
2 |
4 |
2 |
1 |
1 |
17 |
3 |
1 |
2 |
2 |
3 |
3 |
3 |
2 |
2 |
18 |
7 |
2 |
1 |
3 |
4 |
2 |
3 |
5 |
4 |
19 |
8 |
4 |
6 |
3 |
5 |
1 |
4 |
4 |
2 |
20 |
2 |
3 |
3 |
4 |
6 |
6 |
3 |
3 |
2 |
21 |
1 |
2 |
2 |
3 |
7 |
1 |
2 |
7 |
1 |
22 |
5 |
4 |
4 |
2 |
8 |
3 |
3 |
2 |
3 |
23 |
4 |
2 |
5 |
3 |
9 |
2 |
4 |
4 |
2 |
24 |
3 |
2 |
6 |
4 |
10 |
5 |
2 |
5 |
5 |
25 |
2 |
3 |
7 |
2 |
11 |
-2 |
2 |
3 |
2 |
26 |
-1 |
3 |
2 |
2 |
12 |
3 |
2 |
-5 |
3 |
27 |
3 |
2 |
-4 |
3 |
13 |
-2 |
3 |
-4 |
2 |
28 |
5 |
3 |
-2 |
2 |
14 |
4 |
3 |
-2 |
1 |
29 |
2 |
2 |
2 |
3 |
15 |
-3 |
2 |
-4 |
3 |
30 |
4 |
2 |
-5 |
3 |
