2 Особенность

В первом уравнении Максвелла присутствуют два тока: ток проводимости и ток смещения. Но, как мы рассматривали ранее, существует еще и ток переноса, плотность которого равна

,

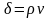где – плотность зарядов, а

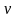– скорость движения этих зарядов.

Ток переноса также создает магнитное поле , поэтому в первом уравнении максвелла в общем случае необходимо записывать все три тока

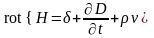. (12)

Но для большинства физических явлений ток переноса играет незначительную роль, поэтому, как правило, его не учитывают.

3 Особенность

При чрезвычайно высоких частотах, когда длина электромагнитной волны становится соизмеримой с линейными размерами, характеризующими молекулярную структуру самого вещества, вещество уже нельзя рассматривать как непрерывное.

В этом случае уравнения Максвелла должны быть заменены уравнениями квантовой теории поля.

4 Особенность

В изотропных средах, характеристики которых не зависят от направления, вектор электрического смещения совпадает по направлению с вектором напряженности электрического поля и вектор плотности тока 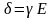также совпадает с вектором , а вектор магнитной индукции 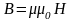совпадает по направлению с вектором напряженности магнитного поля.

В изотропных средах 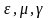представляют собой постоянные числа, не зависящие от величины электрических и магнитных полей, но зависящие от частоты.

Если вектора заданы своими координатами

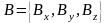а 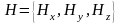, то для изотропных сред выполняются соотношения

.

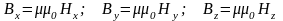Для электрического поля выполняются аналогичные соотношения

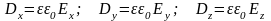
В анизотропных средах вектор электрического смещения не совпадает по направлению с вектором напряженности электрического поля и вектор плотности тока также не совпадает с вектором , а вектор магнитной индукции не совпадает по направлению с вектором напряженности магнитного поля.

Любая проекция векторов 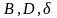зависит не только от одноименной проекции векторов и , но и от других проекций этих векторов, т.е.

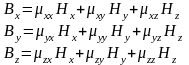
Т.е. магнитная проницаемость представляет собой тензор третьего ранга

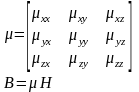
65. Чем обусловлен комплексный характер диэлектрической проницаемости на высоких частотах электромагнитного поля?

комплексный характер диэлектрической проницаемости обусловлен проводимостью среды

65. В чем заключается упрощение системы уравнений Максвелла при выводе на основе этих уравнений волновых уравнений?

Переменное электромагнитное поле создается токами и зарядами, зависящими не только от координат. Но и от времени. Рассмотрим, каким уравнениям подчинятся векторный и скалярный потенциалы 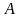и 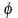в переменном электромагнитном поле. С этой целью запишем систему уравнений максвелла

. (1)

. (2)

. (3)

. (4)

; (5)

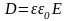. (6)

, (7)

и дополним эту систему уравнением непрерывности

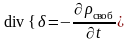. (8)

и уравнением, которое связывает вектор магнитной индукции и векторный потенциал магнитного поля

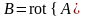. (9)

Умножим первое уравнение Максвелла на 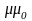. Тогда получим

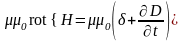. (10)

Поднесем под знак ротора слева, а справа вместо вектора электрического смещения запишем вектор напряженности электрического поля

.

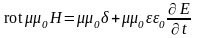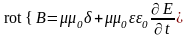
Учитывая, что 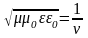, где v – фазовая скорость электромагнитной волны, получаем, что

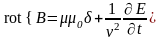. (11)

Подставим в последнее уравнение выражение для индукции магнитного поля через векторный потенциал магнитного поля (9)

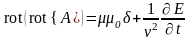
Раскроем операцию двойного ротора, как мы делали уже неоднократно

.

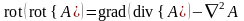Тогда

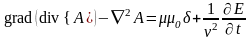. (13)

Теперь во второе уравнение Максвелла подставим выражение для индукции магнитного поля через векторный потенциал магнитного поля (9)

.

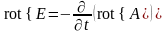Так как ротор является только функцией пространственных координат, то можно поменять в последнем выражении очередность операций производной и ротора.