35. Біноміальний розподіл.

Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:

При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:

.

Імовірнісна твірна функція для біноміального закону

.

Основні числові характеристики:

.

;

.

_________________________________

35. Закон розподілу неперервної випадкової величини. Рівномірний розподіл.

Цілочислова випадкова величина Х має рівномірний закон розподілу, якщо ймовірності її можливих значень обчислюються за формулою:

. (1)

Імовірнісна твірна функція:

.

Числові характеристики:

.

_________________________________

35. Нормальний розподіл.

Випадкова величина Х має нормальний закон розподілу ймовірностей, якщо

f (х) = ,

де а = М (X),  =  (X). Отже, нормальний закон визначається звідси параметрами а і  і називається загальним.

Тоді

F(x)=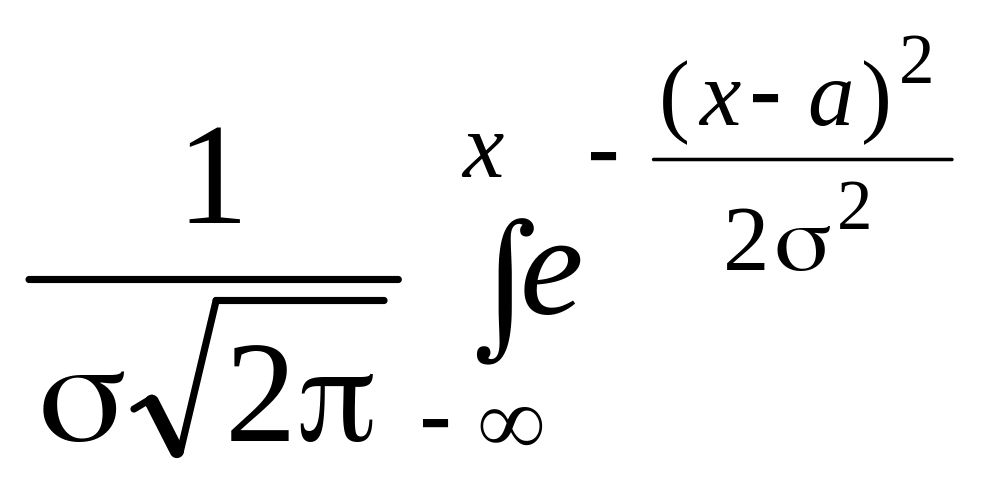 dx. (2)

Для нормального закону Мо=Ме=а.

Загальний нормальний закон позначають: N (a; ).

_________________________________

35. Правило трьох сигм для нормального закону.

Коли , то маємо:

.

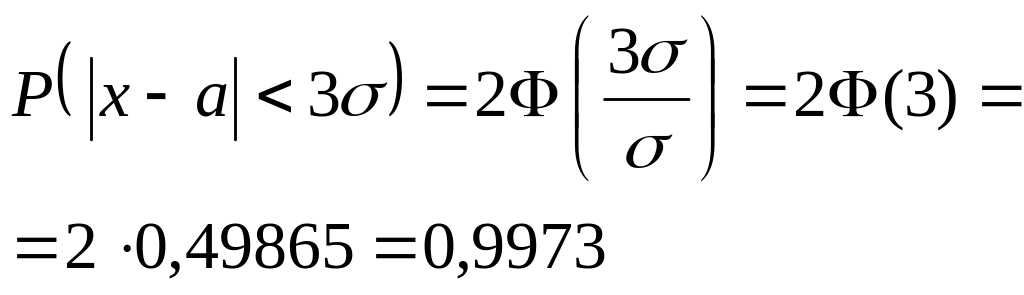Практично ця подія при одному експерименті здійсниться, а тому її вважають практично вірогідною. Звідси:

Тобто ймовірність того, що внаслідок проведення експерименту випадкова величина Х, яка має закон розподілу N (a; ), не потрапить у проміжок , дорівнює 0,0027.

_________________________________

35. Геометричний закон.

Закон подається формулою:

Геометричний закон розподілу має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У формулі р — імовірність настання події в кожному випробуванні. Геометричний закон розподілу застосовується у задачах статистичного контролю якості і теорії надійності. Числові характеристики розподілу:

_________________________________

35. Розподіл х2.

Розглядаємо послідовність попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.

Якщо то ця сума має розподіл з ступенями волі. Щільність розподілу

Числові характеристики розподілу:

M(X)=n. D(X)=2n.

_________________________________

35. Математичне сподівання і дисперсія при нормальному розподілу.

Нормальний розподіл — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності

Нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль.

Математичне сподівання нормального розподілу дорівнює параметру а: М(Х) = а.

Дисперсія при нормальному розподілі: D(Х) = σ².

_________________________________

35. Ймовірність влучення в заданий інтервал при нормальному розподілі.

Нормальний розподіл — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності

Ймовірність влучення в заданий інтервал при нормальному розподілі:

Р (α<х<β) = Ф - Ф ,

де Ф(х) = - функція Лапласа.

_________________________________

35. Математичне сподівання і дисперсія при показовому розподілу.

Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)

Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування.

Числові характеристики:

_________________________________

35. Ймовірність влучення в заданий інтервал при показовому розподілі.

Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)

Функція розподілу показового закону:

Ймовірність влучення в заданий інтервал при показовому розподілі:

Р(а < X < b) = F(b) – F(a) =1 – e ^–λb – (1 – e ^-λa ) = e ^-λa – e ^-λb

_________________________________

35. Показовий розподіл.

Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)

Показовий розподіл визначається одним параметром λ. Ця особливість має перевагу в порівнянні з розподілами, що залежать від більшого числа параметрів.

Функція розподілу показового закону:

_________________________________

35. Елементи математичної статистики. Вибірковий метод.

Центральним поняттям статистики є поняття статистичної сукупності, як маси деяких однорідних елементів, що відрізняються між собою за певними ознаками. Одиниці сукупності, з яких складається статистична сукупність, надалі будемо називати елементами цієї сукупності.

Встановлення статистичних закономірностей, щодо масових випадкових явищ, ґрунтується на вивченні статистичних даних – відомостей про те, які значення прийняла окрема ознака унаслідок проведення досліду.

На практиці статистичних досліджень відрізняють два види дослідів: суцільний і вибірковий.

Вся сукупність елементів, яку треба вивчити називається генеральною сукупністю. Та частина об’єктів, що її відібрано для безпосереднього вивчення із генеральної сукупності, називається вибірковою сукупністю.

Сутність вибіркового методу полягає в тому, щоб за деякою частиною генеральної сукупності робити висновки про її властивості в цілому.

Щоб за даними вибірки мати можливість судити про генеральну сукупність, вона повинна бути взята випадково.

Розрізняють наступні види вибірок:

• власне-випадкова вибірка, отримана випадковим відбором елементів без поділу їх на частини або групи;

• механічна вибірка, для якої елементи генеральної сукупності відбираються через деякий інтервал;

• типова вибірка, у яку випадковим чином вибираються елементи з типових груп, на які за деякою ознакою поділяється генеральна сукупність;

• серійна вибірка, у яку випадковим чином потрапляють не елементи груп, а власне групи, які потім суцільно досліджуються.

_________________________________