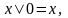1)Информация, алфавит, буква, слово, длина слова. Понятие информации, данных. Хар-ка инфы. Св-ва инфы. Аспекты инфы.

Понятие "информация" имеет различные трактовки в разных предметных областях., информация может пониматься как:

абстракция,

сигналы для управления,

мера хаоса

вероятность выбора

мера разнообразия.

алфавит –множество знаков, , для которых определена операция конкатенации (приписывания)с ее помощью получают слова и словосочетания в этом алфавите

Буквой – элемент x алфавита X, где . Понятие знака неразрывно связано с тем, что им обозначается ("со смыслом"), они вместе могут рассматриваться как пара элементов (x, y), где x – сам знак, а y – обозначаемое этим знаком.

Конечная последовательность букв алфавита называется- словом в алфавите (или над алфавитом).

Длиной |p| некоторого слова p над алфавитом Х называется число составляющих его букв.

Слово (обозначаемое символом Ø) имеющее нулевую длину, называется пустым словом: |Ø| = 0.

Множество различных слов над алфавитом X обозначим через S(X) и назовем словарным запасом (словарем)

алфавит должен позволять решать задачу лексикографического упорядочивания, или задачу расположения слов над этим алфавитом, в соответствии с порядком, определенным в алфавите

Информация – это некоторая упорядоченная последовательность сообщений, отражающих, передающих и увеличивающих наши знания.

Классификации информации:

Информация актуализируется с помощью различной формы сообщений – определенного вида сигналов, символов.

Информация трех типов: входная, выходная и внутренняя.

Информация по отношению к конечному результату исходная, промежуточная и результирующая.

Информация по ее изменчивости бывает постоянная, переменная и смешанная.

Информация по стадии ее использования бывает первичная и вторичная.

Информация по полноте бывает избыточная, достаточная и недостаточная.

Информация по доступу к ней бывает открытая и закрытая.

Свойства информации:

полнота;

актуальность;

адекватность;

понятность;

достоверность;

массовость;

устойчивость;

ценность и др.

Основные св-ва информации,:

-Объективность и субъективность. -Полнота-достаточность данных для принятия решений.

-Достоверность—уровень посторонних сигналов, зарегистрированных в полезном сигнале.

-Адекватность—соответствия реальному состоянию дела.

-Доступность-возможности получит

-Актуальность-степень соответствия текущему моменту.

Семантический аспект информации—характеристика информации с точки зрения смысла, содержания. Смысловую сторону информации изучает семантика, являющаяся разделом семиотики — науки о знаках и знаковых системах.

Прагматический аспект информации — характеристика с точки зрения полезности, пригодности для решения задачи. оценка может быть субъективной, отражая точку зрения получателя Проблемы прагматического отбора информации изучает прагматика — раздел семиотики, науки о знаках и знаковых системах. Исследования важны для проектирования информационно-поисковых систем, машинного перевода и др.

2)Методы получения инфы. Характеристика метода можно разбить на три большие группы.

Эмпирические методы

Теоретические методы

Эмпирико-теоретические методы (смешанные)

эмпирические методы.

Наблюдение – сбор первичной информации

Сравнение –соотнесение общего и различного.

Измерение – поиск с помощью приборов эмпирических фактов.

Эксперимент – рассмотрение с целью выявления новых св.

теоретические методы.

Восхождение от абстрактного к конкретному – получение знаний о целом или о его частях на основе знаний об абстрактных проявлениях в сознании, в мышлении.

Идеализация – получение знаний о целом или его частях путем представления в мышлении целого или частей, не существующих в действительности.

Формализация – получение знаний о целом или его частях с помощью языков искусственного происхождения

Аксиоматизация – получение знаний о целом или его частях с помощью некоторых аксиом 5.Виртуализация – получение знаний о целом или его частях с помощью искусственной среды, с

эмпирико-теоретические

Абстрагирование – выделение наиболее важных для исследования свойств, сторон.

Анализ – разъединение целого на части с целью выявления связи

Декомпозиция – разъединение целого на части с сохр связей с окружающей средой

Синтез – соединение частей в целое для выявления их взаимосвязи.

Композиция — соед частей целого с сохр их взаимосвязей с окружением.

Индукция – получение знания о целом по знаниям о частях.

Дедукция – получение знания о частях по знаниям о целом.

Эвристики, использование эвристических процедур – получение знания о целом по знаниям о частях и по наблюдениям, опыту, интуиции, предвидению. Моделирование – получение знания о целом или о его частях с помощью модели.

Исторический метод – поиск знаний с использованием предыстории.

Логический метод – поиск знаний путем воспроизведения частей, связей

Макетирование – получение информации по макету.

Актуализация – получение информации с помощью перевода целого или его частей из статического состояния в динамическое состояние.

Визуализация – получение информации с помощью наглядного или визуального представления состояний объекта, процесса, явления.

3)Система счисления. Представление чисел в различных системах. Перевод целых чисел из одной в другую.

Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр.

(унарная, непозиционные и позиционные).

Унарная – это система счисления, в которой для записи чисел используется только один знак

непозиционных наиболее распространенной римскую систему счисления. базовые: 1—I, 5—V,10—X,50—L100—С,500—D,1000—М. Все другие числа строятся комбинаций базовых по правилам:

если стоит справа от большей цифры, то суммируются; если слева — то вычитается

цифры I, X, С и М следовать подряд не более трех раз каждая;

цифры V, L и D не более одного раза.

Позиционными -в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Наиболее 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Однако в истории человечества имеются — пятеричной, шестеричной, двенадцатеричной, двадцатеричной и шестидесятеричной

Представление чисел в различных системах счисления

не зависит от способа его представления и остается одинаковым во всех системах счисления; различаются только формы представления с одного и того же количественного содержания числа

4)Высказывания и предикаты. Алгебра, высказывание, предикат, булевское, высказывание, логические функции.

Алгебра–наиболее адекватный математический аппарат описания действий наилучшим образом подходит для описания информационных.Информационные процессы хорошо формализуются с помощью различных алгебраических структур.

Алгеброй A называется некоторая совокупность элементов X, с заданными над ними операциями f которые удовлетворяют свойствам – аксиомам алгебры.

Операция f называется n-местной, если она связывает n операндов

Совокупность операций алгебры A называется ее сигнатурой, а совокупность элементов алгебры – носителем алгебры.

Высказывание – некоторое утверждение, про которое можно однозначно сказать истинно или ложно. "истина" и "ложь", "true" и "fаlse" или "1" и "0".

Предикат – высказывательная форма с логическими переменными имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи - местностью.

Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой х – логическая переменная с заданным множеством изменений аргумента, а значения f(x) берутся из двухэлементного множества R(f) = {1,0}.

Множество логических переменных 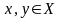с определенными над ним операциями: – отрицания или инверсии, 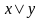– логического сложения или дизъюнкции, – логического умножения или конъюнкции называется алгеброй предикатов

5)Аксиомы алгебры предикат.

Аксиома двойного отрицания: .

Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции): , .

Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов): , .

Аксиомы одинаковых операндов: , .

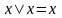Аксиомы поглощения: , .

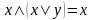Аксиомы распределения операции (дизъюнкции относительно конъюнкции и наоборот)

, .

Аксиомы де Моргана (перенесения бинарной операции на операнды): , .

Аксиомы нейтральности (взаимноинверсных множителей или слагаемых): , .

Аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0), причем, , , , .

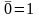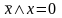Из этих аксиом следует ряд полезных соотношений, например,