25.Производная сложной функции.

Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Производная обратной функции равна обратной величине производной данной функции.

26.Производнаяобратной функции.

Пусть функция   имеет в точке   производную  . Тогда обратная функция   имеет в соответствующей точке   производную  , которую можно отыскать по формуле

(4.14)

 Доказательство.    

Дадим аргументу   приращение  , такое что  , и рассмотрим соответствующее приращение  , определяемое равенством  .

Тогда, очевидно,  ; при этом  , а из монотонности функции   следует, что  . Поскольку как функция  , так и функция   непрерывны, то условия   и   эквивалентны. Составим теперь разностное отношение для функции   и запишем для него очевидное равенство:

Теперь перейдём в этом равенстве к пределу при   и учтём, что при этом   тоже стремится к 0:

что мы и хотели доказать.       Заметим, что, очевидно, из формулы (4.14) следует, что

(4.15)

если   -- функция, обратная к  .

27.Логарифмическая производная.

Отношение  называется логарифмической производной функции f(x)

Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: 

Используя формулу производной сложной функции, найдем, что  (*)

Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.

Пример

Найдём производную функции у = х^x. Поскольку lny= xlnx, легко найти логарифмическую производную:

Теперь с помощью формулы (*) получим:

Логарифмическая производная функции имеет экономический смысл – отношение скорости изменения величины у (ее производной) к самой этой величине – темп изменения у; если темп положителен – скорость изменения увеличивается, если отрицателен –  скорость падает.

28.Производная функции, заданной неявно и параметрически.

Неявно заданная функция

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Пример:

Найти производную функции у, заданную уравнением х³+у³-3ху=0.

Решение: Функция у задана неявно. Дифференцируем по х равенство х³+у³-3ху=0. Из полученного соотношения

3х²+3у² у'-3(1 у+х у')=0

следует, что у²у'-ху'=у-х², т. е. у'=(у-х²)/(у²-х).

Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет

находить производную у'_х от функции заданной

параметрически, не находя непосредственной зависимости у от х.

<< Пример 21.2

Пусть  

Найти у'_х.

Решение: Имеем   x'_t=3t²,   y'_t=2t.   Следовательно,   у'_х=2t/t²,   т. е. 

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно,    Тогда    Отсюда  т. е. 29.Дифференциал функции, инвариантность формы 1- го дифференциала.

Дифференциал функции

Главная линейная часть приращения функции Ax в определении дифференцируемости функции

f=f(x) - f(x0)=A(x - x0)+o (x – x0), xx0

называется дифференциалом функции f(x) в точке x0 и обозначается

df(x0)=f(x0)x= Ax.

Дифференциал зависит от точки x0 и от приращения x. В каждой точке дифференциал представляет собой линейную функцию от приращения x.

Если в качестве функции рассмотреть f(x)=x , то получим dx=x, dy=Adx. Это согласуется с обозначением Лейбница  .

Геометрическая интерпретация дифференциала как приращения ординаты касательной.

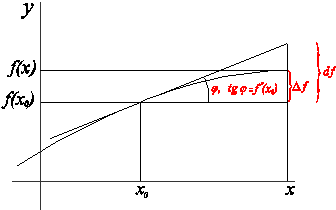
Инвариантность формы первого дифференциала

Если x - независимая переменная, то dx = x - x₀ (фиксированное приращение). В этом случае имеем

df(x₀) = f'(x₀)dx.     (3)

Если x = φ(t) - дифференцируемая функция, то dx = φ'(t₀)dt. Следовательно,

т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.