
- •2 Дидактическое обеспечение
- •4 Инструктаж
- •5 Порядок выполнения
- •6 Методические рекомендации
- •7 Формы контроля (отчета)
- •8 Критерии оценки ипз
- •9 Содержание ипз
- •Приложение а
- •Приложение б
- •Приложение в
- •Правило Лопиталя Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует, т.Е.
Приложение а
Краткий справочник формул, необходимых для выполнения работы
|
- общее уравнение прямой |
|
- уравнение прямой с угловым коэффициентом k |
|
- угловой коэффициент |
|
- условие параллельности прямых |
|
- условие перпендикулярности прямых |
1 Прямая
2 Канонические уравнения кривых второго порядка
Окружность |
|
|
Эллипс |
|
|
|
|
|
Гипербола |
|
|
|
|
|
Парабола |
|
|
|
|
3 Уравнение нормали к кривой в точке (x0,y0)
![]()
Уравнение нормали к кривой в точке (x0,y0)
![]()
Приложение б
Раскрытие неопределённостей по правилу Лопиталя

Приложение в
Образцы выполнения типовых задач
Задание 1
Составить уравнения касательной и нормали к эллипсу
![]() в
точке с ординатой
в
точке с ординатой
![]()
Решение
1) Найдем абсциссу точки:
Для
удобства решения запишим уравнение
эллипса в виде
![]()
![]()
Подставим
значение
![]() в
полученное уравнение
в
полученное уравнение
![]()
![]()
![]() ,
т.к.
,
т.к.
![]() ,
то имеем точку
,
то имеем точку
![]()
2) Найдем угловой коэффициент касательной и нормали:
Найдем производную неявной функции:
![]()

![]()
3) Составим уравнение касательной:
![]()
Упростим
полученное уравнение, помножим обе
части на![]()
![]()
4) Составим уравнение нормали:
![]()
![]() ,
,![]()
Задание 2
Составить уравнение касательной к кривой
![]() ,
,
![]()
1) Найдем координаты точки:
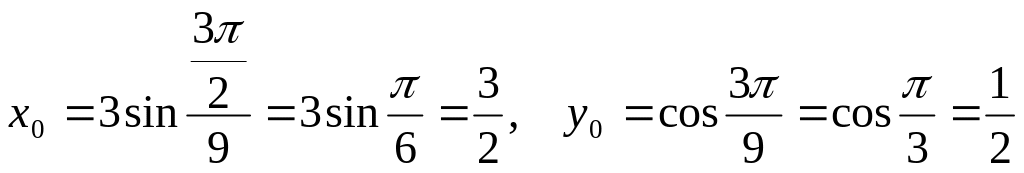 .
.
Имеем
точку
![]()
2) Найдем угловой коэффициент касательной и нормали:
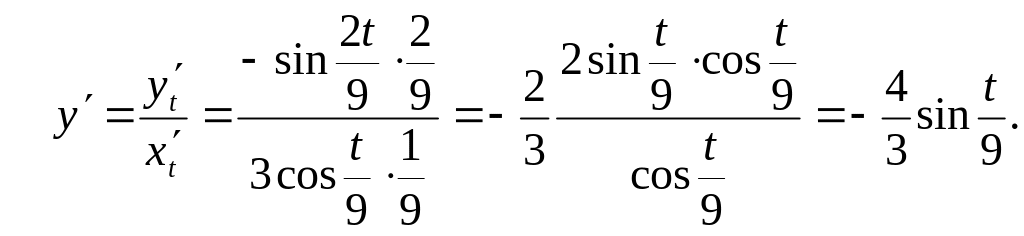
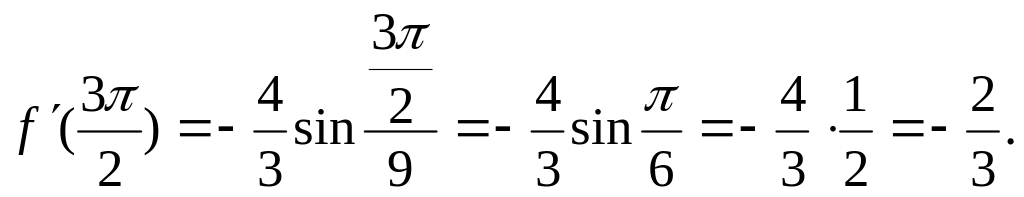
![]()
3) Составим уравнение касательной:
![]() .
.
Задание 3 Раскрыть неопределенности по правилу Лопиталя
Рассмотрим
отношение f(x)=![]() где
функции
где
функции
![]() и
и
![]() определены и дифференцируемы, в некоторой
окрестности точки
определены и дифференцируемы, в некоторой
окрестности точки
![]() исключая, быть может, саму точку
.
Если при х
исключая, быть может, саму точку
.
Если при х![]() обе
функции стремятся к 0 или к
обе
функции стремятся к 0 или к
![]() ,
т.е. эти
,
т.е. эти
функции
одновременно являются бесконечно
малыми или бесконечно большими при х![]() ,
то говорят, что в точке
функция
f(x)
имеет неопределенность, соответственно,
вида
,
то говорят, что в точке
функция
f(x)
имеет неопределенность, соответственно,
вида
![]() .
В этом случае, используя производные
.
В этом случае, используя производные
![]() и
и
![]() ,
можно сформулировать простое правило
для нахождения предела функции f(x)
при х
,
можно сформулировать простое правило
для нахождения предела функции f(x)
при х![]() ,
т.е. дать рецепт для раскрытия
неопределенностей вида
Это правило обычно связывают с именем
французского математика
,
т.е. дать рецепт для раскрытия
неопределенностей вида
Это правило обычно связывают с именем
французского математика
Лопиталя, впервые опубликовавшего его.
