Указания к выполнению задания 2

Приведем примеры раскрытия неопределенностей по правилу Лопиталя.

Пример 1. Вычислить .

Решение. При каждая из функций и

стремится к нулю, поэтому имеет место неопределенность вида . Предел находим по правилу Лопиталя:

.

.

Так как , то воспользуемся теоремой о пределе произведения:

Здесь дважды использовалось правило Лопиталя.

Пример 2. Вычислить .

Решение. При числитель и знаменатель дроби неограниченно возрастают, поэтому неопределенность имеет вид .

.

Здесь возможны два случая. Если , то , поэтому . Если же , то , поэтому .

Пример 3. Вычислить .

Решение. При будет и , поэтому неопределенность имеет вид . Прежде чем применить правило Лопиталя, преобразуем ее к виду следующим образом: . Поэтому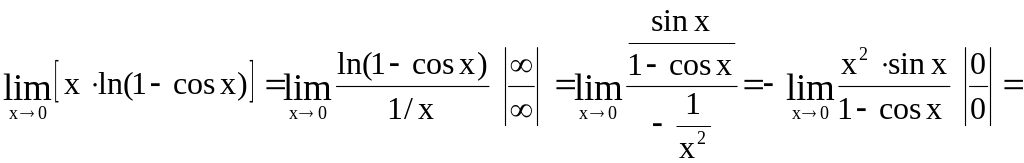

.

Пример 4. Вычислить .

Решение. При будет и , поэтому имеет место неопределенность вида . Преобразуем ее к неопределенности вида

следующим образом: . Поэтому =

Пример 5. Вычислить .

Решение. При и , поэтому имеет место неопределенность вида . Обозначим искомый предел через А, т.е. . Прологарифмируем обе части равенства по основанию е:

. Логарифмическая функция непрерывна в области определения, поэтому знаки и lim можно переставить местами. Тогда получим . Далее по правилу Лопиталя:

.

Итак, , отсюда .

Ответ: .

Пример 6. Вычислить .

Решение. При , поэтому неопределенность имеет вид . Обозначим искомый предел А, т.е. . Прологарифмируем обе части равенства по основанию е:

.

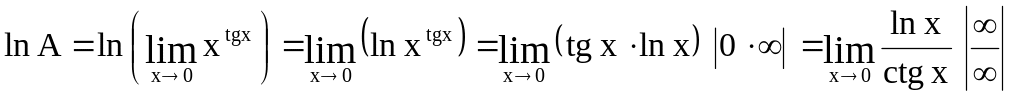Далее по правилу Лопиталя:

.

Итак, , отсюда А=1.

Ответ: .

Пример 7. Вычислить .

Решение. При , поэтому имеет место неопределенность вида . Применим прием, использованный в примерах 5 и 6 : .

.

отсюда А=2.

Ответ: .

Задание 3. Кривизна кривой

Определить кривизну, центр и радиус круга кривизны данной кривой в указанной точке.

1. . 2. .
3. . 4. .
5. . 6. .
7. . 8. .
9. . 10. .
11. . 12. .
13. . 14. .
15. . 16. .
17. . 18. .
19. . 20. .
21. . 22. .
23. . 24. .
25. . 26. .
27. . 28. .
29. . 30. .
31. . 32. .
33. . 34. .
35. . 36. .
37. в ее вершине. 38. в точках, где кривизна наибольшая.
39. в точках экстремума. 40. в точке, где кривизна наибольшая.
41. в точках, где радиус кривизны наименьший. 42. в точках ее пересечения с осью абсцисс.
43. в любой точке кривой. 44. в любой точке кривой.
45. в любой точке кривой. 46. в ее вершине.
47. в точках, где радиус кривизны наименьший. 48. в ее вершине. 49. в ее вершине. 50. в ее вершине.