7. Статически неопределимые задачи при растяжении, сжатии: а) статически неопределимый брус; б)температурные напряжения; в)стержневые системы.

Стат. неопред. задачи имеют место, когда усилие и опорные реакции нельза определить только при помощи ур-я статики.Порядок расчёта:1) Статическая сторона задачи ( -записываем возможные ур-я статики; -опред-я степень стат. Неопределимости S=h-c, c – ур-е статики) 2)Геометр. сторона задачи (-строится план деформации сис-ы и нах-ся связь между деформацией). 3)Физическая сторона задачи (∆l – заменяем через усилие по з. Гука -∆l_i= ) 4) Синтез (решаем совместно ур-я статики и деформации,(с учетом з. Гука) и находим неизв-е.Статически неопределимый брус

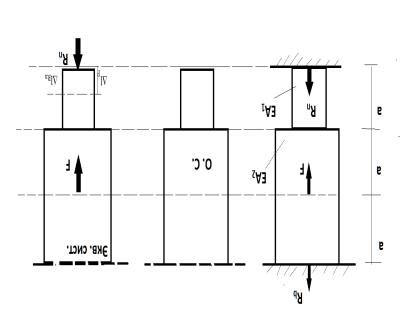
∑z=0 R_n+R_b=F S=2-1=1

Выбираем осн. сист.(для бруса)

Осн. система по S – это стат-и опред-й брус, полученный из заданного путём отбрасывания лишней связи. На основании принципе независимости действия сил получим: ∆l=∆l_F+∆l_Rn=0

∆l_F=

∆l_Rn=- - = - = R_n∙( ) =

2R_n=F/2

R_n=F/4

Температурные напряжения

R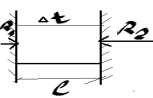 ₁=R₂=R

∆l_t=α∙l∙∆t⁰

α – центр линейного расшир.

материала.

∆l_Rn = = α∙l∙∆t⁰

∆l_Rn=∆l_Rt

∆l_Rt + ∆l_R =0 R= α∙∆t⁰∙E∙A

Ϭ=R/A= α∙E∙∆t⁰ Если есть зазор

∆l=∆

45.Определение максимального прогиба при внецентренном сжатии гибкого стержня. Условие прочности.

Условие прочности:

46.Понятие о расчёте тонкостенных оболочек. Определение напряжений в осесимметрических оболочках по безмоментной теории.

Оболочка тела ограниченная двумя криволинейными поверхностями:

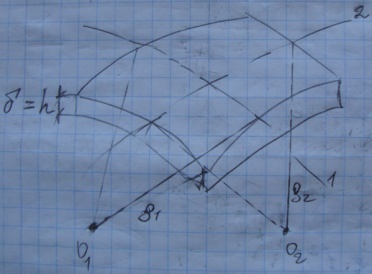
1.N₁, N₂, S₁, S₂. 2.M₁, M₂, T₁, T₂, Q₁, Q₂.

Если _min – тонкая оболочка.

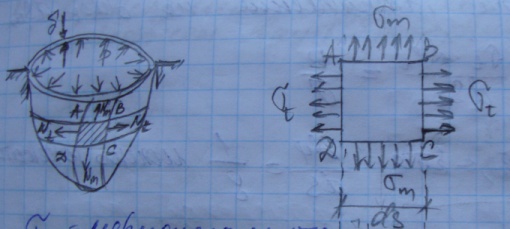
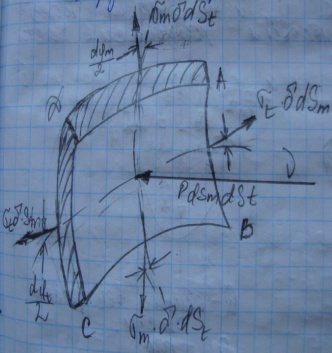
Спроектируем силы на ν: Σν=0;

Разделим это выражение на

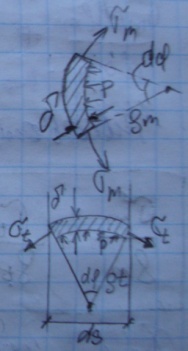
Учитывая, что , можно записать

Д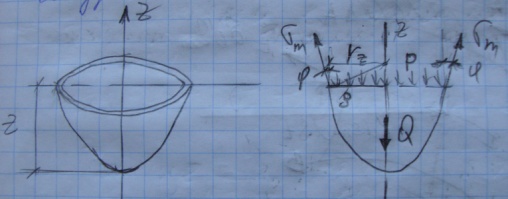 ля нахождения σ_m и σ_t уравнение получим из условия равновесия части сосуда.

; Q- общий вес рассмотренной части

47.Определение напряжений в сферическом и цилиндрическом сосудах. Условие прочности для тонкостенных сосудов.

Рассмотрим сферический сосуд под действием внутр. давления газа.

Рассмотрим цилиндрический котёл под действием равномерного давления газа или пара.

Из уравнения Лапласа:

Условия прочности:

По второй теории:

ν-коэффициент Пуассона.

По третьей теории:

По четвёртой (энергетической) теории:

При определении учитывается марка стали, типы заклёпок или сварные швы. Температура и ряд других факторов.

После расчёта к этой толщине (δ) добавляют 1 2 мм за счёт коррозии.

48.Понятие о расчёте толстостенных труб под действием осесимметрической нагрузки. Напряжения в толстостенной трубе. Задача Ляме.

Рассмотрим криволинейный элемент:

Толщина элемента=1. Спроектируем все силы на радиальное направление:

Преобразуем: слагаемое 2-го рода малости(dσ_rdr) будем считать равным 0.

Ранее известно

Решая совместно эти 2 уравнения найдём

Интегрируя, получим: