
- •18 Статически неопределимые задачи при кручении.
- •19.Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
- •Часть 2.
- •21.Построение эпюр в консольной балке.Диф зависимости.
- •2 3. Определение касательных напряжений при изгибе (формула Журавского)
- •24. Главные напряжения при изгибе.
- •25.Подбор сечений и проверка прочности балок.
- •26.Траектория главн напр.Потенц. Энергия при изгибе.
- •28.Пример определения перемещений в балках
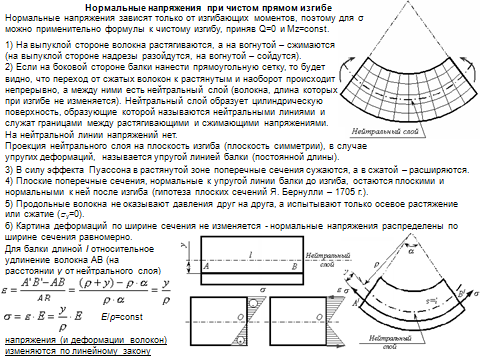
- •22.Определение нормальных напряжений при чистом изгибе
- •29.Графоаналитич. Метод определения перемещений в балках.
- •30.Простейшие статически неопределимые балки. Порядок расчета.
- •50. Определение деформаций и перемещений в толстой трубе. Понятие о расчёте составных цилиндров. Усл прочн.
- •51. Учёт сил инерции при действии динамических нагрузок. Напряжение при ударе.
- •52. Проддольный поперечный и скручивающий удар. Понятие об усталостной прочности
- •7. Статически неопределимые задачи при растяжении, сжатии: а) статически неопределимый брус; б)температурные напряжения; в)стержневые системы.
- •45.Определение максимального прогиба при внецентренном сжатии гибкого стержня. Условие прочности.
- •46.Понятие о расчёте тонкостенных оболочек. Определение напряжений в осесимметрических оболочках по безмоментной теории.
- •47.Определение напряжений в сферическом и цилиндрическом сосудах. Условие прочности для тонкостенных сосудов.
- •48.Понятие о расчёте толстостенных труб под действием осесимметрической нагрузки. Напряжения в толстостенной трубе. Задача Ляме.
26.Траектория главн напр.Потенц. Энергия при изгибе.
Траектория-линия косат. к каждой точке, которая совпадает с направлением главного движения.
.
![]()
Характер траектории зависит от вида нагрузки и от типа опирания.
Потенциальная энергия при изгибе.

![]()
 ;
; ;
;


27.Диф.ур-ие изогнутой оси балки.Метод начальных параметров.


![]() -угол
поворота сечения
-угол
поворота сечения
кривизна известна
известна

![]() <<1
<<1
 ;
;
![]() ;знак
зависит от выбора системы координат:
;знак
зависит от выбора системы координат:

![]() правило
знаков:+ прогиб вверх,угол поворота с +
против хода часовой стрелки.
правило
знаков:+ прогиб вверх,угол поворота с +
против хода часовой стрелки.
Метод начальных параметров:при выводе универсальных ур-ий углов поворота и прогибов исп след. условности:1)начало координат всегда берется на крайнем левом сечении(центр тяжести)
 2)интегрирование
выражений производится без раскрытия
скобок(метод Клебша)
2)интегрирование
выражений производится без раскрытия
скобок(метод Клебша)
3.распр.нагрузка
недоходящая до правого конца балки
продливается и компенсируется такой
же нагрузкой.
4.выражение
момента для сосредоточеного момента
берется с плечом в 0 степени.
![]()
Универсальные
ур-ия для углов поворота:![]() -общий
вид.
-общий
вид.![]() -ур-ие
прогибов,
-ур-ие
прогибов,![]() угол
поворота и прогиб.
угол
поворота и прогиб.![]() начальные
параметры.
начальные
параметры.![]() силовые
ф-ции которые записываются для каждого
случая и учитывают нагрузку действующую
между началом коорд. И сечением z.
Вид этих ф-ий берется из таблицы.
силовые
ф-ции которые записываются для каждого
случая и учитывают нагрузку действующую
между началом коорд. И сечением z.
Вид этих ф-ий берется из таблицы.
Ур-ия
,опр.![]() в произвольном сечении балки:
в произвольном сечении балки:
 Пример:
Пример:
«- « значит прогиб вниз
28.Пример определения перемещений в балках


22.Определение нормальных напряжений при чистом изгибе
29.Графоаналитич. Метод определения перемещений в балках.
θ=Q_фик/〖EI〗_x - угол поворота; y=M_фик/EI – прогиб (*)
〖EI〗_x y- прогиб; 〖EI〗_x y^'- угол поворота; 〖EI〗_x y^''- момент M; 〖EI〗_x M- момент; 〖EI〗_x M^'=Q – поперечная сила; 〖EI〗_x Q^'=q- интенсивность распред. нагрузки.
Порядок расчета:1)строится эп. «М»;2)эп. «М»принимает фиктивн. Нагрузку(нагр. действует к оси балки) и прикладывается к фиктивн. балке;3)Определяется Q_фик и M_фик в задан. сечении;4) определяют Q и y по ф-ле(*)
30.Простейшие статически неопределимые балки. Порядок расчета.
Статич. неопред. бал. – та в которой хотя бы одна лишняя связь, а в них все реакции нельзя определить только из уравнений равновесия. Расчет вести по методу сравнения деформации: 1)определить степень статич. неопред. 2)выбирается основная система;3)записывается ур-ние статики;4)составляется ур-ние прогиба и углов поворота для основн. системы (дополнительно ур-ние деформации);5)решается совместно ур-ние статики и ур-ние деформ.
 -1
раз статически-неопр балка(1 лишняя
связь)
-1
раз статически-неопр балка(1 лишняя
связь)
 -2
раза стат неопр .
-2
раза стат неопр .
Пример: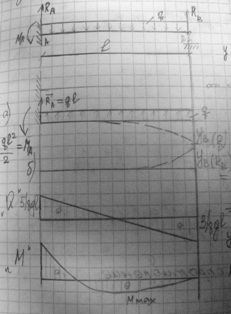

31.Понятие о расчете балок, лежащих на упругом оснавании.
![]() -?
-?
![]() ;
k-коэф.
пропорциональности (коэф. Пастели)
;
k-коэф.
пропорциональности (коэф. Пастели)
![]()
![]()
![]()
![]()
β=![]()
![]()
Решение
этого ур-ния имеет вид:![]()

32.Определение напряжений при косом изгибе.
Кос.изг.- такой вид изг.,когда силовая пл-ть не совпадает не с одной главной осью инерции.
Рассмотр. консольн. балку прямоуг. Сечения
![]()
![]()
![]()
![]()




33.Аналитич.и графич. определение нулевой линии(Н. Л.) при кос. изгибе.
Н.Л.-линия где напряжен. равно нулю.




34.Условие прочности и подбор сечения при кос. изгибе. Определение величины и направления прогиба.
 – усл-е прочности
– усл-е прочности

При подборе сечения:
2)
![]() k=8-10
k=8-10
 k=6-8
k=6-8
3 )
) ![]()
Прогибы:
 ;
;


35.Определение напряжений и построение их эпюр при внецентр. растяж.,сжатии,.
![]()
![]()
Напряж. в любой точке будут равны:

 ;
;


 ;
;
![]() -коор.
точки приложения силы;
-коор.
точки приложения силы;![]() -коорд.
Точки, где определяется напряжение.
(-F)
– сила сжимающая,(+F)-
сила растягивающая.
-коорд.
Точки, где определяется напряжение.
(-F)
– сила сжимающая,(+F)-
сила растягивающая.
36 . Определение положения нул.линии при внецентрен. растяжении, сжат. и ее св-ва.
![]() - урав-ие нулевой линии
- урав-ие нулевой линии
 ;
;

Св-ва Н.Л.:
1)Н.Л.
делит сечение на две зоны сжимающ. и
растягив.2)положение Н.Л. не зависит от
величины действующей силы;3)если сила
приближается к центру тяжести то
Н.Л.будет удалятся от центра тяж. И
наоборот;4)если сила перемещается по
прямой проходящей через центр тяж.
сечения то Н.Л.будет перемещаться
параллельн. самой себе.5)если сила
перемещается по одной из главн. осей
инерции,то Н.Л. перпендикул. этой оси;
6)если Н.Л. перемещается по прямой,
непроходящ. через центр тяж. , то Н.Л.
будет вращаться вокруг некоторой
точки.


37. Что назыв. ядром сечения и цель его построения. Построение ядра сеч. для простых сечений.
Ядро сеч.- область около центра тяж. сечения характерная тем , что приложив к ней и на границе силу напряжения в сечении будут одно знака. Вид ядра зависит от контура.

При построении ядра сечения Н.Л. не должны пересекать сечение.
Для
прямоугольн.![]() ;
;![]()
Для
круга: ![]() ;
;
38. Определение напряж. и расчет на прочность при изгибе и кручении.


![]() –
кручение.
–
кручение.
Расчет на прочность:
![]()


![]()

![]() - условие прочности при изгибе с
кручением.
- условие прочности при изгибе с
кручением.![]() ;
;

39. Понятие об устой-сти сжатых стержней . Определение критической силы. Ф-ла Эйлера.
Устойчивость-способность
элемента сохранять первонач. форму под
действием нагрузки. Сила при которой
стержень находится в неустойчивом
положении наз. Критической, а состояние
критич. ![]() ;
;
![]()
![]()
![]() Решение имеет вид :
Решение имеет вид : ![]() ;определим
;определим
![]() и
и
![]() из
конеч. Условий при z=0
из
конеч. Условий при z=0
![]()
При
z=L![]() ;
;
![]() ;
;
![]() ;
;
![]() k=
k=![]()
![]() где n-число
полуволн синусоиды
где n-число
полуволн синусоиды
![]() -ф-ла
Эйлера
-ф-ла
Эйлера
40. Влияние способов закрепления концов стержня на величину критич.й силы. Пределы применимости ф-лы Эйлера. Критич. напряж. и предельн. гибкость стержня.
 ;
;![]() -
коэф. приведения длины;
-
коэф. приведения длины;![]() ;m-число
полуволн синусоиды
;m-число
полуволн синусоиды
![]() -
приведенная длина
-
приведенная длина

![]() – гибкость стержня;
– гибкость стержня;  ;
;
![]()
 ;
;
![]() -
тогда справедлива ф-ла Эйлера
-
тогда справедлива ф-ла Эйлера

41.
Ф-ла Ясинского для разных материалов.
Диаграмма критич. напряжений для
мягкой стали. Применяется
,когда![]()
![]() для стали а=310,в=1.14Мпа
для стали а=310,в=1.14Мпа
Дерево:а=29.3,
в=0.194
42. Практические расчеты на устойчивость . Проверочный и проектировочный расчеты с использ.таблиц коэф.(φ) .
σ=![]() ;
σ=
;
σ=![]()
![]() ;
; ![]() -
пластичный
-
пластичный
![]() - хрупкий
- хрупкий

![]() (
(![]() -
коэф. запаса на устойчивость)
-
коэф. запаса на устойчивость)
 -
коэф. снижения основного допускаемого
напряжения (коэф. продольного изгиба),
зависит от гибкости и материала.
σ=
-
коэф. снижения основного допускаемого
напряжения (коэф. продольного изгиба),
зависит от гибкости и материала.
σ=![]() ; φ=0÷1
; φ=0÷1
43. Понятие о продольно - попереч. изгибе . ДУ изогнутой оси балки.
Продольн.-поперечн. Изгиб - одновременно приложены сжимающая сила и поперечные нагрузки.
![]() ;
;
![]()
![]() ;
;![]()
![]()
: ![]() ;
;
![]() зависит
от величины
зависит
от величины ![]()
Такое
решение полученного ДУ не всегда удается
получить, поэтому на практике применяют
приближенное значение с достаточной
точностью.
17Анализ напряжённого состояния при кручении. В поперечном и в продольном сечениях круглого стержня при кручении возникают касательные напряжения. На двух взаимно перпендикулярных площадках, одна из которых лежит в плоскости поперечного сечения, а другая- в плоскости продольного сечения, действуют только касательные напряжения. Такое напряжённое состояние называется чистым сдвигом. Траектория этих напряжений представляет винтовую линию, наклонную под углом 45 к образующей.

Характер разрушения материалов при кручении:если материал плохо сопротивляется max касат. напряжениям(дерево), то разрушение происходит по образующей
 2.если
материал плохо сопротивляется
растягивающим сопр.
2.если
материал плохо сопротивляется
растягивающим сопр.
![]() (чугун), то разрушение происходит по
винтовой поверхности от действия
.
(чугун), то разрушение происходит по
винтовой поверхности от действия
.
 3.пластичные
материалы(сталь) при кручении разрушаются
по нормальным сечениям от действия
касательных напряжений
3.пластичные
материалы(сталь) при кручении разрушаются
по нормальным сечениям от действия
касательных напряжений

Расчёт
на прочность и жёсткость.-
условие прочности:
 ,
гд
,
гд![]() -наибольший
крутящий момент по абсолютной величине,
а
-наибольший
крутящий момент по абсолютной величине,
а
![]() -полярный
момент сопротивления
-полярный
момент сопротивления

-
условие жёсткости:
 ,
где
,
где![]() -
относительный угол закручивания;
-
относительный угол закручивания;![]() ;
;


 ;
;
. 49. Труба под действием только внутренего и только наружного давления.
Под действием только внутренего давления:
Р1=Р, Р2=0

![]() ,
,![]() ,
,![]() ,
,![]()

Под действием только наружного давления.
Р1=0,
Р2=Р,![]() ,
,![]() ,
,![]() ,,
,,
![]() .
.
Проверка
прочности: ![]()
![]() =
=![]()
![]()
