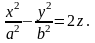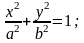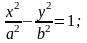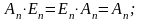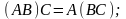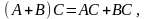- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
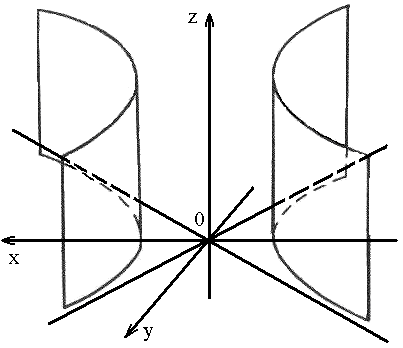
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
59. Поверхности второго порядка
Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид
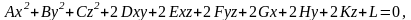 (22)
(22)
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями:
1. Эллипсоид:
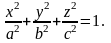
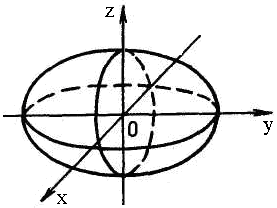
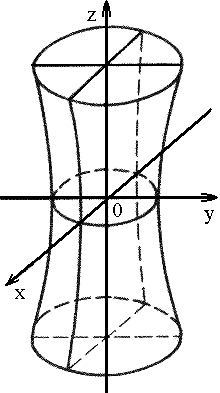
2. Гиперболоид
1) однополостный:
|
2) двуполостный:
|
3. Конус
второго порядка:
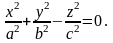
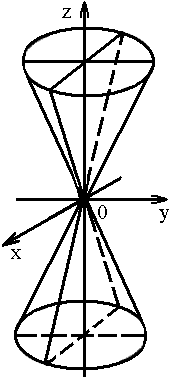
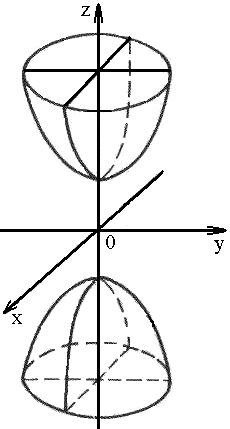
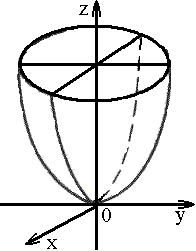
4. Параболоид
1) эллиптический:
|
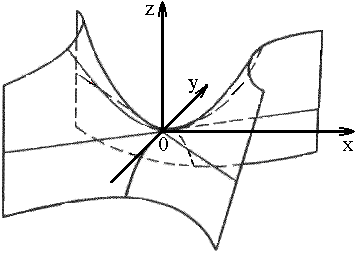
2) гиперболический:
|
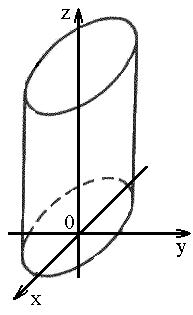
5. Цилиндр
1) эллиптический:
|
2) гиперболический:
|
3) параболический:
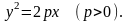
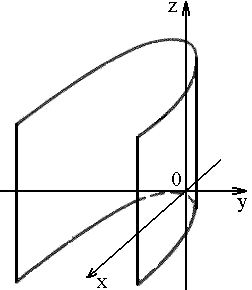
Основным методом исследования формы поверхности является метод сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о виде поверхности. Таким образом изучаются основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в
общем уравнении поверхности коэффициенты
 приведение к каноническому виду
осуществляется с помощью метода выделения
полных квадратов.
приведение к каноническому виду
осуществляется с помощью метода выделения
полных квадратов.
В определенных случаях уравнение (22) поверхности может быть приведено к уравнениям, задающим так называемые вырожденные поверхности. Приведем примеры таких случаев.
 – пустое множество
точек (мнимый эллипсоид);
– пустое множество
точек (мнимый эллипсоид);
 – точка (0, 0, 0);
– точка (0, 0, 0);
 – пустое множество
точек (мнимый эллиптический цилиндр);
– пустое множество
точек (мнимый эллиптический цилиндр);
 –прямая (ось Oz);
–прямая (ось Oz);
 – пара пересекающихся
плоскостей;
– пара пересекающихся
плоскостей;
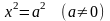 – пара параллельных
плоскостей;
– пара параллельных
плоскостей;
 – пустое множество
точек;
– пустое множество
точек;
 – плоскость (пара
совпадающих плоскостей).
– плоскость (пара
совпадающих плоскостей).
60. Матрицы и действия над ними
Матрицей
называется
прямоугольная таблица, составленная
из элементов некоторого множества.
Горизонтальные ряды такой таблицы
называются строками
матрицы, а вертикальные – ее столбцами.
Матрицы обозначают A,
B,
C,
X
… . Запись aij
используется
для указания местоположения элемента
матрицы (i
– номер строки, j
– номер столбца ). Числовую матрицу
размера
 (то есть состоящую из m
строк и n
столбцов чисел) в общем случае записывают
в виде
(то есть состоящую из m
строк и n
столбцов чисел) в общем случае записывают
в виде
 или в более
компактной форме
или в более
компактной форме
 ,
,
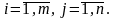
Ee
обозначают также
 .
.
При
 матрицу называют квадратной
и обычно обозначают An.
Элементы aii,
матрицу называют квадратной
и обычно обозначают An.
Элементы aii,
 такой матрицы образуют ее главную
диагональ.
такой матрицы образуют ее главную
диагональ.
Квадратная матрица вида
 ,
(1)
,
(1)
где
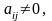
 ,
называется диагональной. Если
,
называется диагональной. Если
 для любого
,
то матрица (1) называется единичной
и обозначается En.
для любого
,
то матрица (1) называется единичной
и обозначается En.
Верхней и нижней треугольной матрицами называются квадратные матрицы вида
 или
или
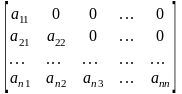 соответственно.
соответственно.
Трапециевидной матрицей называется матрица вида
 ,
где числа a11,
a12,
…, akk
отличны от нуля.
,
где числа a11,
a12,
…, akk
отличны от нуля.
Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.
Две матрицы одинакового размера
 и
и
 (2)
(2)
называются равными,
если
 для всех
для всех
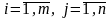 .
.
Суммой матриц (2)
называется матрица A+B
размера m×n,
состоящая из элементов
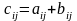 ,
где
.
,
где
.
Произведением
матрицы Am×n
на число α называется матрица
 .
.
Разностью матриц (2) называется матрица A–B = A+ (–1)B.
Свойства опреаций сложения матриц и умножения на число:


0·A=О;



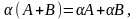
 A
и B
– матрицы одинакового размера.
A
и B
– матрицы одинакового размера.
Для матриц A и B может быть введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.
Произведением
матрицы Al×m
на матрицу Bm×n
называется матрица
 элементы которой
элементы которой

Свойства операции умножения матриц:
В общем случае из
существования AB
не следует существование BA.
Даже если оба эти произведения определены,
они не всегда равны. Матрицы, для которых
 называются коммутативными.
называются коммутативными.
Пусть A
– квадратная матрица. Тогда k-я
степень ( )
матрицы A
определяется равенством
)
матрицы A
определяется равенством
 .
По определению принимают
.
По определению принимают
 при условии
при условии

Матрица AT
, полученная из матрицы A
заменой столбцов строками с теми же
номерами, называется транспонированной
к матрице A,
то есть
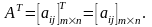
Свойства операции транспонирования матриц:
Если для квадратной
матрицы A
выполняется соотношение
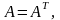 то матрица A
называется симметрической
матрицей, а если
то матрица A
называется симметрической
матрицей, а если
 – то кососимметрической.
– то кососимметрической.
Элементарными преобразованиями над строками матрицы A называют следующие операции:
перестановку строк;
умножение строки на ненулевое число;
прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.
Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.