58. Кривые второго порядка: эллипс, парабола, гипербола

1. Эллипсом называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

(21)

где . (22)

Уравнение (21) называется каноническим уравнением эллипса.

Параметры эллипса:

Точки F₁(–c, 0) и F₂(c, 0), где называются фокусами эллипса, при этом величина 2c определяет междуфокусное расстояние.

Точки А₁(–а, 0), А₂(а, 0), В₁(0, –b), B₂(0, b) называются вершинами эллипса, при этом А₁А₂ = 2а образует большую ось эллипса, а В₁В₂ – малую, – центр эллипса.

Рис. 12

Основные параметры эллипса, характеризующие его форму:

ε = с/a – эксцентриситет эллипса;

– фокальные радиусы эллипса (точка М принадлежит эллипсу), причем r₁ = a + εx, r₂ = a – εx;

– директрисы эллипса.

Для эллипса справедливо: директрисы не пересекают границу и внутреннюю область эллипса, а также обладают свойством

Эксцентриситет эллипса выражает его меру «сжатости».

2. Если b > a > 0, то эллипс также задается уравнением (21), для которого вместо условия (22) выполняется условие

. (23)

Тогда 2а – малая ось, 2b – большая ось, – фокусы (рис. 13). При этом r₁ + r₂ = 2b, ε = c/b, директрисы определяются уравнениями

Рис. 13

При условии имеем (в виде частного случая эллипса) – окружность радиуса R = a. При этом с = 0, а значит, ε = 0.

Точки эллипса обладают характеристическим свойством: сумма расстояний от каждой из них до фокусов есть величина постоянная, равная 2а (рис. 12).

3. Для параметрического задания эллипса (21) в случаях (22) и (23) в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на эллипсе, и положительным направлением оси Ox:

где

4. Если центр эллипса с полуосями находится в точке , то его уравнение имеет вид

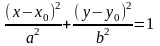. (24)

Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

(25)

где .

Параметры гиперболы:

Точки F₁(–c, 0), F₂(c, 0), где называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние. Точки А₁(–а, 0), А₂(а, 0) называются вершинами гиперболы, при этом А₁А₂ = 2а образует действительную ось гиперболы, а В₁В₂ = 2b – мнимую ось (В₁(0, –b), B₂(0, b)), О – центр гиперболы.

Рис. 19

Величина называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;

– фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r₁ = a + εx, r₂ = –a + εx для точек правой ветви гиперболы, r₁ = – (a + εx), r₂ = – (–a + εx) – для точек левой ветви;

– директрисы гиперболы;

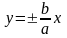– уравнения асимптот.

Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством

Говорят, что уравнение

(26)

задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде

.

В таком случае ось мнимая, фокусы лежат на оси . Все остальные параметры определяются аналогично как для гиперболы (25).

Рис. 20

Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).

Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:

Параболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

Параметры параболы:

Точка F(p/2, 0) называется фокусом параболы, величина p – параметром, точка О(0, 0) – вершиной. При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

Рис. 24

Величина где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина называется эксцентриситетом параболы.

Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 24).

Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 25).:

Рис. 25

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:

где t – произвольное действительное число.