- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
56. Уравнение прямой в пространстве
Пусть
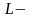 прямая,
уравнение которой необходимо записать,
прямая,
уравнение которой необходимо записать,
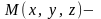 произвольная
точка этой прямой.
произвольная
точка этой прямой.
Если известны
координаты ее направляющего вектора
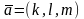 и некоторой фиксированной точки
этой прямой, то
и некоторой фиксированной точки
этой прямой, то
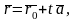 (12)
(12)
где
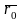 – радиус-вектор точки
– радиус-вектор точки
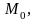
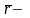 радиус-вектор
произвольной точки,
радиус-вектор
произвольной точки,
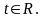 ,
векторно-параметрическое
уравнение.
В координатной форме уравнение (12)
равносильно трем параметрическим
уравнениям:
,
векторно-параметрическое
уравнение.
В координатной форме уравнение (12)
равносильно трем параметрическим
уравнениям:
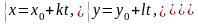 (13)
(13)
Система (13) определяет параметрические уравнения прямой.
По исходной информации получаем канонические уравнения прямой:
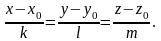 (14)
(14)
Пусть известны 2
точки
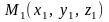 и
и
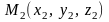 ,
лежащие на прямой
.
Тогда векторы
,
лежащие на прямой
.
Тогда векторы
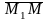 ,
,
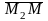 коллинеарны и можно записать уравнение
прямой, проходящей через две точки:
коллинеарны и можно записать уравнение
прямой, проходящей через две точки:
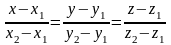 .
(15)
.
(15)
В пространстве прямую можно задать как линию пересечения двух плоскостей:
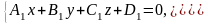 (16)
(16)
В уравнениях плоскостей (16) коэффициенты при переменных не являются пропорциональными.
О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.
Прямые параллельны при условии коллинеарности их направляющих векторов (координаты пропорциональны).
Прямые перпендикулярны при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).
Угол между прямыми можно определить через косинус угла между направляющими векторами.
Прямые лежат в
одной плоскости при условии компланарности
их направляющих векторов и вектора
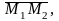 где
где
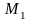 и
и
 – точки этих прямых (смешанное произведение
равно 0).
– точки этих прямых (смешанное произведение
равно 0).
Расстояние от точки до прямой L
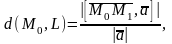 (17)
(17)
где – направляющий вектор, – точка прямой.
Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.
Если прямые и являются скрещивающимися, то расстояние между ними
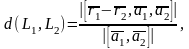 (18)
(18)
где
и
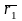 – радиус-векторы точек
и
– радиус-векторы точек
и
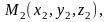 принадлежащих прямым
и
соответственно, а векторы
и
принадлежащих прямым
и
соответственно, а векторы
и
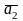 – их направляющие векторы.
– их направляющие векторы.
56. Уравнение прямой и плоскости в пространстве
Пусть прямая L задана каноническими уравнениями:

где
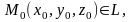
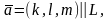 а плоскость P
задана общим уравнением:
а плоскость P
задана общим уравнением:
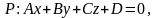
где
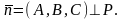
Тогда взаимное
расположение прямой L
и плоскости P
в пространстве можно определить по
взаимному расположению направляющего
вектора
прямой L
и нормальному вектору
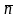 плоскости P:
плоскости P:
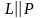 тогда и только
тогда, когда
тогда и только
тогда, когда
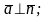
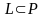 тогда и только
тогда, когда
тогда и только
тогда, когда
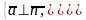
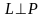 тогда и только
тогда, когда
тогда и только
тогда, когда
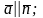
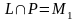 тогда и только
тогда, когда
тогда и только
тогда, когда
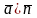 .
В последнем координаты
точки пересечения
могут быть найдены следующим образом.
От канонических уравнений прямой следует
перейти к параметрическим, после чего
подставить найденные значения
.
В последнем координаты
точки пересечения
могут быть найдены следующим образом.
От канонических уравнений прямой следует
перейти к параметрическим, после чего
подставить найденные значения
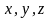 в уравнение плоскости. Затем надо
разрешить полученное уравнение
относительно параметра t
и найденное значение
в уравнение плоскости. Затем надо
разрешить полученное уравнение
относительно параметра t
и найденное значение
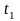 подставить в параметрические уравнения.
Это позволит найти значения
подставить в параметрические уравнения.
Это позволит найти значения
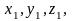 которые и будут координатами искомой
точки
пересечения прямой L
и плоскости P.
которые и будут координатами искомой
точки
пересечения прямой L
и плоскости P.
Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость, т. е.