
- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
45. Векторы, линейные операции над векторами
Под вектором
на плоскости
понимают направленный отрезок с началом
в точке А
и концом в точке B,
который обозначается
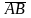 (или
(или
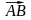 ).
Модулем,
или длиной,
).
Модулем,
или длиной,
 такого
вектора называется длина отрезка
такого
вектора называется длина отрезка
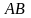 .
.
Если нет необходимости
указывать начало и конец вектора, то
его обозначают
 или
или
 ,
….
,
….
Различают
векторы связанные
(закрепленные),
то есть с фиксированным началом, и
свободные.
Под свободным вектором
 понимают класс эквивалентных направленных
отрезков, т. е. таких отрезков, которые
совмещаются при параллельном переносе.
понимают класс эквивалентных направленных
отрезков, т. е. таких отрезков, которые
совмещаются при параллельном переносе.
Векторы
и
 называются коллинеарными
(обозначение:
называются коллинеарными
(обозначение:
 ),
если они лежат на параллельных прямых.
Кроме того, если они имеют одинаковое
направление, их называют сонаправленными
(обозначение:
),
если они лежат на параллельных прямых.
Кроме того, если они имеют одинаковое
направление, их называют сонаправленными
(обозначение:
 ),
а если противоположное – противоположно
направленными
(обозначение:
),
а если противоположное – противоположно
направленными
(обозначение:
 ).
).
Два вектора
 называются равными,
если они
имеют одинаковые длины и являются
сонаправленными. Записывается это с
помощью обычного знака равенства:
называются равными,
если они
имеют одинаковые длины и являются
сонаправленными. Записывается это с
помощью обычного знака равенства:
 .
При этом запись
.
При этом запись
 понимают также в смысле, что начало
свободного вектора
приложено к точке А.
понимают также в смысле, что начало
свободного вектора
приложено к точке А.
Вектор нулевой
длины называется нулевым
и обозначается
 .
Направление такого вектора считается
неопределенным. У нулевого вектора
начальная и конечная точки совпадают.
.
Направление такого вектора считается
неопределенным. У нулевого вектора
начальная и конечная точки совпадают.
Пусть заданы два
ненулевых вектора
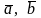 .
Отложим их от некоторой точки О
таким образом,
чтобы
.
Отложим их от некоторой точки О
таким образом,
чтобы
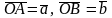 .
Под углом
.
Под углом
 между
векторами
и
понимают наименьший угол, на который
надо повернуть вектор
,
чтобы его направление совпало с
направлением вектора
.
Этот угол
не зависит от выбора точки О
и изменяется
от 0 до .
между
векторами
и
понимают наименьший угол, на который
надо повернуть вектор
,
чтобы его направление совпало с
направлением вектора
.
Этот угол
не зависит от выбора точки О
и изменяется
от 0 до .
Для векторов
определены следующие линейные
операции:
умножение вектора на действительное
число и сложение векторов
 .
.
Произведением вектора на действительное число λ называется вектор , удовлетворяющий следующим условиям:
|λ | = |λ| | |;
λ ↑↑ , если λ > 0,
λ ↑↓ , если λ < 0,
λ = , если λ = 0 или = .
Для того чтобы
сложить векторы
и
геометрически,
используют правило
треугольника:
начало вектора
совмещается с концом вектора
,
их суммой является вектор
 ,
начало которого совпадает с началом
вектора
,
а конец – с концом вектора
(рис. 1). Для обозначения этого действия
используется обычный знак суммы:
,
начало которого совпадает с началом
вектора
,
а конец – с концом вектора
(рис. 1). Для обозначения этого действия
используется обычный знак суммы:
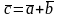 .
.

Рис. 1
Сложение двух векторов можно производить также по правилу параллелограмма: векторы и приводятся к общему началу, некоторой точке О, и на них строится параллелограмм. Тогда суммой этих векторов является вектор , который совпадает с диагональю построенного параллелограмма, исходящей из точки О (рис. 2).

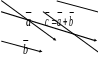
Рис. 2
Сумма трех и более
векторов
 может быть
найдена по правилу
ломаной (замыкающей).
Это вектор, начало которого совпадает
с началом вектора
может быть
найдена по правилу
ломаной (замыкающей).
Это вектор, начало которого совпадает
с началом вектора
 ,
а конец – с концом вектора
,
а конец – с концом вектора
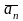 (рис. 3).
(рис. 3).

Рис. 3
Свойства линейных операций над векторами:
коммутативность сложения векторов, т. е.
 ;
;
ассоциативность сложения векторов, т. е.
 ;
;
дистрибутивность сложения векторов относительно умножения на действительное число λ, т. е.
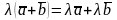 ;
;
дистрибутивность сложения действительных чисел относительно умножения на вектор, т. е.
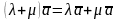 ;
;
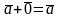 ;
; ;
;коммутативность и ассоциативность операции умножения вектора на число, т. е.
 .
.
Вектор
 называется противоположным
вектору
.
называется противоположным
вектору
.
Разностью векторов и называется вектор
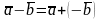 .
.
Для того чтобы
найти разность
 ,
необходимо: привести векторы
и
к общему началу. Тогда разностью
является вектор, у которого начало
совпадает с концом вектора
,
а конец - с
началом
вектора
(рис. 4).
,
необходимо: привести векторы
и
к общему началу. Тогда разностью
является вектор, у которого начало
совпадает с концом вектора
,
а конец - с
началом
вектора
(рис. 4).

Рис. 4
Таким образом,
геометрически векторы
 и
изображаются
диагоналями параллелограмма, построенного
на векторах
и
,
которые приведены к общему началу (рис.
5):
и
изображаются
диагоналями параллелограмма, построенного
на векторах
и
,
которые приведены к общему началу (рис.
5):
 ,
,

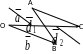
Рис. 5
Вектор
 называется ортом
(единичным
вектором)
вектора
,
если
называется ортом
(единичным
вектором)
вектора
,
если
 и
и
 .
Для его нахождения может быть использована
формула
.
Для его нахождения может быть использована
формула
 .
.
Вектор
называется линейной
комбинацией
векторов
 ,
если
существуют числа
,
если
существуют числа
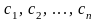 такие, что
такие, что
 ,
,
 .
.
Говорят,
что точка C
делит вектор
 в отношении λ
(λ
> 0), если
в отношении λ
(λ
> 0), если
 =λ
=λ .
.
