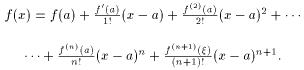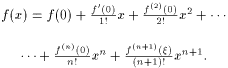- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
42. Формула Тейлора для функции
Теорема
8 (теорема Тейлора). Пусть функция
f(x) имеет в точке x = a и некоторой
ее окрестности производные порядка
n+1. Тогда между точками a и x
a найдется такая точка
![]() ,
что справедлива следующая формула:
,
что справедлива следующая формула:
|
(10) |
Формула (10) называется формулой Тейлора, а выражение
![]()
представляет остаточный член в форме Лагранжа. Заметим, что если функция f(n+1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)n. Таким образом, остаточный член можно записать в виде
Rn+1(x) = o((x-a)n) при x a.
Данная форма записи остаточного члена называется формой Пеано.
Формулой Маклорена называется формула Тейлора при a = 0:
|
(11) |
Остаточный член в форме Пеано для формулы Маклорена имеет вид
Rn+1 = o(xn) при x 0.
Приведем разложения некоторых элементарных функций по формуле Маклорена
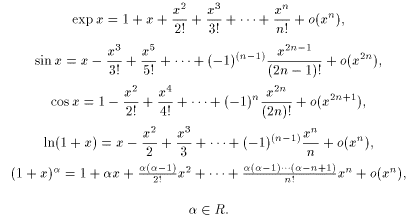
43. Комплексные числа. Алгебраическая форма записи комплексного числа
Число вида
 (10)
(10)
где
а,
 i
– мнимая
единица,
определяемая равенством
i
– мнимая
единица,
определяемая равенством
 называется
комплексным
числом.
называется
комплексным
числом.
Число а
называется действительной
частью
комплексного числа z
и обозначается
 ;
b
называется мнимой
частью
комплексного числа z
и обозначается
;
b
называется мнимой
частью
комплексного числа z
и обозначается
 Запись комплексного числа в виде (10)
называется алгебраической
формой
комплексного числа.
Запись комплексного числа в виде (10)
называется алгебраической
формой
комплексного числа.
Если
 то комплексное число называется чисто
мнимым;
при
то комплексное число называется чисто
мнимым;
при
 получается действительное число.
получается действительное число.
Множество всех
действительных чисел обозначают
 .
Имеет место:
.
Имеет место:
 .
.
В прямоугольной
декартовой системе координат комплексное
число
 изображается точкой M
с абсциссой a
и ординатой b
(рис. 9). Между множеством всех точек
координатной плоскости и множеством
всех комплексных чисел существует
взимно-однозначное соответствие.
Координатная плоскость называется
комплексной
плоскостью.
Ось абсцисс называется действительной
осью, ось
ординат – мнимой
осью.
изображается точкой M
с абсциссой a
и ординатой b
(рис. 9). Между множеством всех точек
координатной плоскости и множеством
всех комплексных чисел существует
взимно-однозначное соответствие.
Координатная плоскость называется
комплексной
плоскостью.
Ось абсцисс называется действительной
осью, ось
ординат – мнимой
осью.
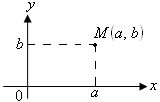
Рис. 9
Два комплексных
числа
 и
и
 называются равными,
если соответственно равны их действительные
и мнимые части:
называются равными,
если соответственно равны их действительные
и мнимые части:

Если
то число
 называется сопряженным
числу z
и обозначается
называется сопряженным
числу z
и обозначается


Сопряженные числа
в системе координат изображаются
точками, симметричными относительно
оси

44. Действия над комплексными числами в алгебраической форме
Действия над комплексными числами в алгебраической форме
Пусть

 тогда:
тогда:
 (11)
(11)
 (12)
(12)
 (13)
(13)
Формулы (11) – (13)
показывают, что операции сложения,
вычитания и умножения выполняются
аналогично таким же действиям над
многочленами (с учетом
 при умножении).
при умножении).
Для нахождения
частного комплексных чисел
 и
и
 сначала числитель и знаменатель дроби
сначала числитель и знаменатель дроби
 умножают на сопряженное знаменателю
число
умножают на сопряженное знаменателю
число
 а затем производят остальные действия:
а затем производят остальные действия:
 (14)
(14)
Свойства комплексно-сопряженных чисел
1)

2)

3)

4)

5)

6)