9. Отношения. Бинарные отношения. Основные понятия (определение, обозначения, область определения, область значений, способы задания бинарных отношений). Привести примеры.

Отношения это один из способов задания взаимосвязи между элементами множества. ОТНОШЕНИЕ - подмножество конечной декартовой степени   данного множества А, т. е. подмножество систем (a₁, а₂,.., a _п).из пэлементов множества А.

Подмножество   наз. п- местным, или n-арным, отношением в множестве А. Число n наз. рангом, или типом, отношенияR. Подмножество   наз. также n-местным, или n-арным, предикатом на множестве А . Запись  означает, что  .Одноместные О. наз. свойствами. Двуместные О. наз. бинарными, трехместные О. - тернарными и т. д.

R называют бинарным отношением на множестве A, если  . При этом вместо записи   часто используют запись xRy.

Если   то говорят, что R определено на паре множеств A и B.

Множество всех первых элементов пар из R называется областью определения отношения R и обозначается как  .

Множество всех вторых элементов пар из R называется областью значения отношения R и обозначается как  .

Инверсия(Обратное отношение) R — это множество   и обозначается, как R ^{− 1}.

Способы задания бинарных отношений

Существует четыре разных способа задания отношений, а преимущества каждого проявляются при разных характеристиках множества X.

Первый, очевидный, способ состоит в 1 непосредственном перечислении таких пар. Ясно, что он приемлем лишь в случае конечного множества R.

Второй удобный способ задания отношения R на конечном множестве — матричный. Все элементы нумеруются, и матрица отношения R определяется своими элементами для всех i и j. Известным примером такого задания отношений являются турнирные таблицы (если ничьи обозначить нулями, как и проигрыш, то матрица изобразит отношение «x_i — победитель y_j»).

Третий способ — задание отношения — 1 графом. Вершинам графа G(R) ставят в соответствия (пронумерованные) элементы множества X, и если x_iRy_j, то от вершины x_i проводят направленную дугу к вершине x_j.

Для определения отношений на бесконечных множествах альтернатив используется четвертый способ — задание отношения R - 1 сечениями. Множество называется верхним сечением отношения, а множество

R^-(x) = {y ∈ X | (y,x) ∈ R}

нижним сечением. Иначе говоря, верхнее сечение — это множество всех y, которые находятся в отношении xRy с заданным элементом x, а нижнее сечение — множество всех y, с которыми заданный элемент x находится в отношении R. Отношение однозначно определяется одним из своих сечений.

Пример: С - множество всех членов семьи. С={a,b,c,d,e}a-отец,b-мать,c,d,e-дети. R={(x,y)/”x есть отец y”, x, y прин. C}, R={(a,c),(a,d),(a,e)}

A={1,2} B={0,3} A*B={(1;0),(1;3),(2;0),(2;3)} a<b R={(a;b)/a<b, a прин А, в прин В} R={(1;3),(2;3)}

10. Отношения. Свойства бинарных отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность). Привести примеры.

Отношения это один из способов задания взаимосвязи между элементами множества. ОТНОШЕНИЕ - подмножество конечной декартовой степени   данного множества А, т. е. подмножество систем (a₁, а₂,.., a _п).из пэлементов множества А.

Подмножество   наз. п- местным, или n-арным, отношением в множестве А. Число n наз. рангом, или типом, отношенияR. Подмножество   наз. также n-местным, или n-арным, предикатом на множестве А . Запись  означает, что  .Одноместные О. наз. свойствами. Двуместные О. наз. бинарными, трехместные О. - тернарными и т. д.

Бинарные отношения могут обладать различными свойствами, такими как

• Рефлексивность:  В математике бинарное отношение R на множестве X называется рефлексивным, если всякий элемент этого множества находится в отношении R с самим собой.

Формально, отношение R рефлексивно, если  .

Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент имеет петлю — дугу (х, х).

• Антирефлексивность: 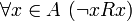 Если это условие не выполнено ни для какого элемента множества X, то отношение R называется антирефлексивным.

Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).

Формально антирефлексивность отношения R определяется как:  .

Если условие рефлексивности выполнено не для всех элементов множества X, говорят, что отношение R нерефлексивно.

• Симметричность:  В математике бинарное отношение R на множестве X называется симметричным, если для каждой пары элементов множества (a,b) выполнение отношения   влечёт выполнение отношения  .

Формально, отношение R симметрично, если  .

• Антисимметричность:  В математике бинарное отношение R на множестве X называется антисимметричным, если для каждой пары элементов множества a,b выполнение отношений aRb и bRaвлечёт a = b, или, что то же самое, выполнение отношений aRb и bRa возможно только для равных a и b. Формально, отношение R антисимметрично, если 

• Транзитивность: 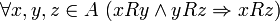 В математике бинарное отношение R на множестве X называется транзитивным, если для любых трёх элементов множества a,b,c выполнение отношений aRb и bRc влечёт выполнение отношения aRc.

Формально, отношение R транзитивно, если  .

Примеры рефлексивных отношений

отношения эквивалентности:

отношение равенства 

отношение сравнимости по модулю

отношение параллельности прямых и плоскостей

отношение подобия геометрических фигур;

отношения нестрогого порядка:

отношение нестрогого неравенства 

отношение нестрогого подмножества 

отношение делимости 

[править]Примеры антирефлексивных отношений

отношение неравенства 

отношения строгого порядка:

отношение строгого неравенства 

отношение строгого подмножества 

отношение перпендикулярности прямых (или ортогональности ненулевых векторов) в геометрии.

Пример:

Любое отношение эквивалентности, по определению, является симметричным (а также рефлексивным и транзитивным). Также симметрично отношение связи вершин графа(неориентированного).

Не являются симметричными (за исключением случая тождественной ложности отношения) отношения порядка (как полного, так и частичного), а также отношение следования вершин ориентированного графа. Однако, отношение сравнимости для частичного порядка является, по построению, симметричным (хотя, в отличие от самого́ порядка, не транзитивным).

Равенство: a = b и b = c, значит a = c (на самом деле, отношение равенства вместе с отношением эквивалентности и параллельности прямых обладает более сильным свойством также ещё и «равенства третьему» по причине своей симметричности)