
- •Универсальное множество: Универсальное множество (универсум) — множество, содержащее все мыслимые объекты. Упорядоченное множество — множество, на котором задано отношение порядка.
- •Множество. Способы задания множеств (перечислением или списком, порождающей процедурой, описанием характеристического свойства). Привести примеры.
- •Объединение более чем двух множеств. Пусть дано семейство множеств Тогда его объединением называется множество, состоящее из всех элементов всех множеств семейства:
- •Алгебра множеств. Законы алгебры множеств. Доказать один из законов алгебры множеств.
- •Множество. Мощность множества. Нахождение мощности объединения множеств (для двух множеств, для трех множеств, для n-множеств). Привести пример.
- •Векторы. Прямое произведение множеств. Мощности прямого произведения множеств.
- •Отношения. Основные понятия отношений (отношения; унарные, бинарные, n-местные отношения)
- •Отношения. Бинарные отношения. Основные понятия (определение, обозначения, область определения, область значений, способы задания бинарных отношений). Привести примеры.
- •Способы задания бинарных отношений
- •Отношения. Свойства бинарных отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность). Привести примеры.
- •Переключательные (булевы) функции. Происхождение булевых функций.
- •Булевы функции от одного аргумента. (Определение. Все булевы функции от одного аргумента).
- •Булевы функции от двух аргументов (Определение булевой функции двух аргументов, тождественный ноль, тождественная единица, конъюнкция, штрих Шеффера, дизъюнкция, стрелка Пирса (функция Вебба)).
- •Свойства дизъюнкции, конъюнкции и отрицания (теорема 4.3).
- •Свойства эквиваленции, импликации и отрицания (теорема 4.4).
- •Выражение одних булевых функций через другие (теорема 4.5).
- •Булевы функции от n аргументов (определение, равенство булевых функций, суперпозиция булевых функций). Булевы функции от n переменных
- •Булевы функции и формулы алгебры высказываний.
- •Нормальные формы булевых функций.
- •Применение булевых функций к релейно-контактной схеме. Две основные задачи теории релейно-контактных схем.
- •Релейно-контактные схемы в эвм. Двоичный полусумматор. Одноразрядный двоичный сумматор.
- •Графы. Основные понятия и определения (вершины, ребра, петли, кратность ребра, псевдограф, мультиграф, граф, орграф, неориентированный граф). Привести примеры.
- •Графы. Матричное задание графов. Матрица смежности, матрица инцидентности. Привести примеры.
- •Графы. Свойства матрицы смежности и инцидентности. Утверждение о числе всех путей (маршрутов) длины k из одной вершины в другую. Утверждение о наличие хотя бы одного контура.
- •Графы. Связность. Компоненты связности. (Достижимость вершины, связный (сильно связный орграф) граф, слабо связанный, несвязанный, компонента связности (сильной связности)). Привести примеры.
- •Графы. Матрицы связности. Утверждение о матрицах связности, матрицы достижимости, матрицы сильной связности.
- •Графы. Поиск путей (маршрутов) с минимальным числом дуг (ребер). Алгоритм фронта волны.
- •Графы. Минимальные пути (маршруты) в нагруженных орграфах (графах). Алгоритм Форда-Беллмана.
Векторы. Прямое произведение множеств. Мощности прямого произведения множеств.
Вектор (или
кортеж) - это упорядоченный набор
элементов. Например, ![]() .
Элементы вектора называются координатами или компонентами.
Число координат - длина вектора (размерность).
.
Элементы вектора называются координатами или компонентами.
Число координат - длина вектора (размерность).
Координаты вектора могут
совпадать ![]() .
.
Два вектора равны,
если они имеют одинаковую длину и равны
соответствующие координаты: ![]() и
и ![]()
![]()
Проекцией вектора ![]() на
ось
на
ось ![]() (
( ![]() )
называется его i-я компонента.
)
называется его i-я компонента. ![]()
Проекцией вектора ![]() на
оси с номерами
на
оси с номерами ![]() называется вектор
называется вектор ![]() длины
длины ![]() .
.
Пример: ![]() ,
,
![]()
![]()
![]()
Прямое произведение
Прямым
(декартовым) произведением множеств ![]() и
и ![]() (
( ![]() )
называется множество всех векторов
)
называется множество всех векторов ![]() ,
таких, что
,
таких, что ![]() :
:
![]()
Если ![]() ,
то
,
то ![]() .
Аналогично для нескольких множеств. Прямым
произведением множества
.
Аналогично для нескольких множеств. Прямым
произведением множества ![]() называетсямножество всех векторов длины
называетсямножество всех векторов длины ![]() ,
таких, что
,
таких, что ![]() .
.
![]()
Примеры.
Множество
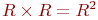 - множество точек
плоскости, точнее пар вида
- множество точек
плоскости, точнее пар вида  ,
где
,
где  и
являются координатами.
и
являются координатами.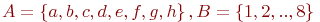 .
.
Тогда ![]() - множество всех
64 клеток шахматной доски.
- множество всех
64 клеток шахматной доски.
- множество букв, символов, знаков препинания и т. д. Тогда элементы множества
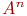 -
слова длины
.
Множество всех слов
-
слова длины
.
Множество всех слов 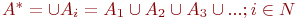 составляет
язык.
составляет
язык.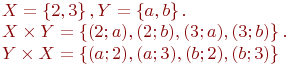 .
.
Следовательно, ![]() .
.
Теорема о мощности прямого произведения
Пусть ![]() -
конечные множества.
Соответственно мощности этих множеств равны:
-
конечные множества.
Соответственно мощности этих множеств равны: ![]() .
.
Тогда мощность прямого
произведения
множеств равна
произведению мощностей соответствующих множеств,
т.е. ![]() .
.
Доказательство методом математической индукции.
Для ![]() теорема
тривиально верна. Предположим, что она
верна и для
теорема
тривиально верна. Предположим, что она
верна и для ![]() и
докажем ее справедливость для
и
докажем ее справедливость для ![]() .
.
По предположению ![]() .
Возьмем любой вектор
.
Возьмем любой вектор ![]() из
из ![]() и
припишем справа элемент
и
припишем справа элемент ![]() .
Это можно сделать
.
Это можно сделать ![]() способом,
т. е. получим
различных векторов из
способом,
т. е. получим
различных векторов из ![]() .
.
Таким образом, из
всех ![]() векторов приписыванием
справа элемента из
векторов приписыванием
справа элемента из ![]() можно
получить
можно
получить ![]() векторов,
причем все они различны. Поэтому
для
теорема
верна и, следовательно, верна для любых
.
векторов,
причем все они различны. Поэтому
для
теорема
верна и, следовательно, верна для любых
.
Следствие: ![]()
Отношения. Основные понятия отношений (отношения; унарные, бинарные, n-местные отношения)
Отношения это
один из способов задания взаимосвязи
между элементами множества. ОТНОШЕНИЕ -
подмножество конечной декартовой
степени ![]() данного
множества А, т.
е. подмножество систем (a1,
а2,.., a п).из
пэлементов множества А.
данного
множества А, т.
е. подмножество систем (a1,
а2,.., a п).из
пэлементов множества А.
Подмножество ![]() наз. п- местным,
или n-арным, отношением в множестве А. Число
n наз. рангом, или типом,
отношенияR. Подмножество
наз. п- местным,
или n-арным, отношением в множестве А. Число
n наз. рангом, или типом,
отношенияR. Подмножество ![]() наз.
также n-местным, или n-арным, предикатом
на множестве А
. Запись
наз.
также n-местным, или n-арным, предикатом
на множестве А
. Запись ![]() означает,
что
означает,
что ![]() .Одноместные
О. наз. свойствами. Двуместные О. наз.
бинарными, трехместные О. - тернарными
и т. д.
.Одноместные
О. наз. свойствами. Двуместные О. наз.
бинарными, трехместные О. - тернарными
и т. д.
В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется непустое множество упорядоченных пар элементов этого множества. Бинарное отношение R из множества А в множество В называется подмножества прямого произведения А и В.
По существу одноместное (унарное) отношение есть подмножество некоторого множества М. Установить на М унарное отношение означает приписать некоторым его элементам признак R.
На языке теории множеств и алгебры n-местным отношением называется множество (класс) упорядоченных систем из n элwементов (упорядоченных n-ок, соответственно — упорядоченных пар) членов некоторого множества. Это множество назвается полем данного отношения.
Если, например, упорядоченная пара (х, у) принадлежит некоторому отношению R, то говорят также, что х находится в отношении R к у (символически: R(xy) или xRy).
