10.Определение угла наклона прямой к плоскости

Длину отрезка АВ и - угол наклона отрезка к плоскости П₁ можно определить из прямоугольного треугольника АВС   |AС|=|A₁B₁|, |BС|=Z. Для этого  на эпюре (рис.31) из точки B₁  под углом 90⁰ проводим отрезок |B₁B₁*|=Z, полученный в результате построений отрезок A₁B₁* и будет натуральной величиной отрезкаАВ, а угол B₁A₁B₁*=. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П₁, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций».

а) модель			б) эпюр
Рисунок 31. Определение натуральной величины отрезка и угла его  наклона к горизонтальной плоскости проекций

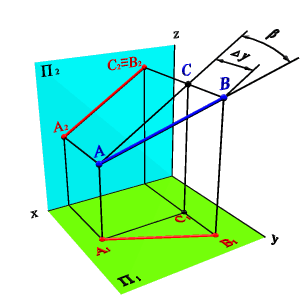
    Длину отрезка АВ и -угол наклона  отрезка к плоскости П₂ можно определить из прямоугольного треугольникаАВС   |AС|=|A₂B₂|, |BС|=Y. Построения аналогичные рассмотренным, только в треугольнике АВВ* сторона|BВ*|= и треугольник совмещается с плоскостью П₂ (рис.32).

а) модель		б) эпюр
Рисунок 32. Определение натуральной величины отрезка и угла его к фронтальной плоскости

11.Определение расстояния от точки до прямой

ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ

Для того чтобы определить расстояние от точки до прямой, необходимо из точки опустить на прямую перпендикуляр. Прямого решения эта задача не имеет, так как прямой угол между прямыми общего положения будет проецироваться с искажением.

Проведем через точку М плоскость , перпендикулярную прямой 1 (рис.10.4). Зададим эту плоскость двумя пересекающимися прямыми - горизонталью и фронталью. В этом случае горизонтальная проекция горизонтали будет перпендикулярна горизонтальной проекции прямой1. Фронтальная проекция фронтали - перпендикулярна фронтальной проекции прямой 1. Рис. 10.4.

Построим точку встречи прямой 1 с плоскостью , l = К. Так как прямая 1 перпендикулярна плоскости , следовательно, она перпендикулярна любой прямой, принадлежащей плоскости , в том числе - и прямой МК, т.е. прямая МК перпендикулярна прямой 1.

Отрезок МК спроецировался с искажением. Его натуральную величину найдем способом вращения вокруг фронтально проецирующей прямой, проходящей через точку М. M₁K₁ = MK .

Решение задачи методом проецирования на дополнительную плокость приведено на рис.10.5 в следующем разделе. M₅K₅ = MK .