
- •1.Классическое определение вероятности
- •2.Геометрическое определение вероятности
- •6 7Б 3ч 4б 6ч 2б 8ч . Формула полной вероятности
- •8.Схема с повторением испытаний (схема Бернулли)
- •12. Числовые характеристики св. Математическое ожидание.
- •49. Интервальные оценки параметров распределения
- •18.Биномиальный закон распределения вероятности
- •19. Равномерный закон распределения случайных величин
- •36.Классификация смо
- •38. Время обслуживания.
- •39. Смо с отказами.
- •22 .Показательный закон
- •40 Система уравнений Эрланга
- •41 Установившийся режим работы смо
- •43 Смо с ограниченной очередью ожидания
- •23.Нормальный закон
- •21.Поток событий
- •13. Дисперсия и ско, свойства
- •14. Плотность вероятности непрерывной св
- •15.Функция распределения случайной величины.
- •16.Связь между f(X) и f(X) для непрерывной св.
- •Вопрос 32: теорема Бернулли.
- •Вопрос 33:Центральная предельная теорема.
- •Вопрос 35: Основные элементы смо.
- •Вопрос 34: Доказательство интегральной формулы Муавра-Лапласа.
41 Установившийся режим работы смо
Примем за начальный момент времени начало работы СМО.
Очевидно Р0(0) = 1, Р1(0) = Р2(0) =…= Рn(0) =0
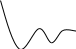
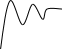
Далее с течением времени вероятности состояний меняются в соответствии с системой уравнений Эрланга. Анализ системы Эрланга показывает, что это изменение носит характер, указанный на рисунке. В течение небольшого периода времени после начала работы СМО вероятности состояний могут сильно меняться. Этот период называется переходным режимом работы СМО. С течением времени вероятности состояний стабилизируются, становятся практически постоянными. Этот период называется установившимся режимом работы СМО.
P0(t) P1 (t) Pn(t)

 1
1
1
1
1
1
P P
P
0 t 0 t t
Вероятности состояний в установившемся режиме называются финальными вероятностями:
P0, P1, … , Pn.
Для практики представляет интерес анализ работы СМО главным образом в установившемся режиме. Мы знаем, что производная постоянной равна нулю. Поэтому в установившемся режиме
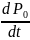 =
=
 =…=
=…=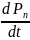 =
0
=
0
42.Показатели эффективности для СМО с отказом.
Показатели эффективности для СМО с отказами:
Р0 – вероятность простоя СМО, то есть вероятность того, что все каналы обслуживания свободны.
Р ОТК – вероятность отказа, то есть вероятность того, что требование, поступившее в СМО застанет все каналы обслуживания занятыми и покинет его, то есть процент требований, получивших отказ и покидающих СМО.
А – абсолютная пропускная способность СМО, то есть среднее число требований, которое может обслужить СМО, за единицу времени.
Р обс – Вероятность обслуживания или относительная пропускная способность, то есть отношение среднего числа требований, обслуживающих СМО в единицу времени, к среднему числу поступивших требований за это же время
. – среднее число занятых каналов.
43 Смо с ограниченной очередью ожидания
СМО с ограниченной очередью ожидания удовлетворяет тем же первым четырём условиям, что СМО с отказами, а пятое условие заменяется следующим: если в момент поступления требования в СМО все каналы обслуживания заняты, требование становится в очередь и ждёт обслуживания. Число мест в очереди ограничено и равно I. требование, поступившее в момент, когда все места в очереди заняты, к обслуживанию не принимается и покидает СМО.
Из
данного определения вытекает, что СМО
с ограниченной очередью ожидания
определяется четырьмя параметрами:
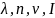 (
(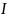
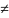 0).
0).
В каждый момент времени t СМО находится в одном из следующих состояний:
о череди
нет
череди
нет
S0- ноль занятых каналов (все каналы свободны);
S1- один канал занят, остальные свободны;
………………………………………….
Sn- n каналов заняты.
очередь есть
S n+1-
n
каналов заняты,
одна заявка в очереди;
n+1-
n
каналов заняты,
одна заявка в очереди;
……………………………………………
Sn+1-n каналов заняты, I заявок в очереди.
Обозначим Pk(t)- вероятность состояния Sk в момент t (k= 0, 1, …, n+I)
Используя соображения, приведённые при выводе системы уравнений Эрланга для СМО с отказами, можно вывести систему дифференциальных уравнений для вероятностей Pk (t). Анализ этой системы показывает, что со временем Pk (t) стабилизируются, становятся практически независимыми во времени:
Pk
(t)
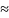 Pk
= const, k=0, 1,…, n, n+1,…, n+I,
Pk
= const, k=0, 1,…, n, n+1,…, n+I,
т о
есть наступает установившийся режим,
вероятности Р0,
Р1,…,Рn+I
является финальными
вероятностями. Учитывая
Pk
(t)
Pk
= const,
k=0,
1,…, n,
n+1,…,
n+I,
система дифференциальных уравнений
для Pk
(t)
в установившемся режиме, аналогично
Po
=
P1;
о
есть наступает установившийся режим,
вероятности Р0,
Р1,…,Рn+I
является финальными
вероятностями. Учитывая
Pk
(t)
Pk
= const,
k=0,
1,…, n,
n+1,…,
n+I,
система дифференциальных уравнений
для Pk
(t)
в установившемся режиме, аналогично
Po
=
P1;
P1 = 2 P2;
P2 = 3 P3;
Pn-1 = n Pn;
P0+P1+…+Pn =1 принимает вид:
P0 = P1;
P1 =2 P2;
…………………..
Pn-1 =n Pn;
Pn =n Pn+1;
Pn+1 =n Pn+2;
………………………..
Pn+I-1 =n Pn+1;
P0+P1+…+Pn+1 =1
Разрешая эту систему, получаем следующие формулы для финальных вероятностей:
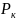 =Р0
=Р0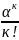 ,
(к
= 1,…, n).
,
(к
= 1,…, n).
Pn+s=P0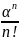 (
(
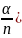 S,
(S = 1,…, I).
S,
(S = 1,…, I).
Р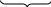 0=
0=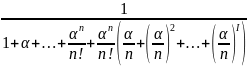
Где
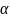 =
=
Просуммировав подчеркнутую в скобках геометрическую прогрессию, получим для вычисления Р0:
P0=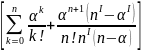 -1
(степень)
-1
(степень)
Итак, =Р0 , (к = 1,…, n). Pn+s=P0 ( S, (S = 1,…, I).
Р0=
P0= -1 (степень)
являются расчётными формулами для вычисления предельных значений вероятностей состояний. Зная эти вероятности, можно найти основные показатели эффективности СМО с ограниченной очередью:
1. Формула P0= -1 (степень) одновременно характеризует вероятность простоя СМО ( все каналы свободны).
2. вероятность отказа в обслуживании. Заявка получает отказ, если все n каналов заняты и все I мест в очереди заняты
Pотк
= Pn+1
=
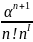 P0
P0
Абсолютная пропускная способность Робс ( доля обслуженных требований, среди всех поступивших на обслуживание) равна вероятности того, что требование будет принято на обслуживание, то есть
Pобс=
1-Ротк=
1-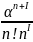 P0
P0
Абсолютная пропускная способность- это среднее число требований, обслуживаемых в единицу времени.
А=
Робс=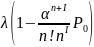
Среднее
число занятых каналов. Как
и раньше обозначим его через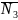 .
Учитывая, что абсолютная пропускная
способность есть произведение
на производительность
одного
канала, получим:
.
Учитывая, что абсолютная пропускная
способность есть произведение
на производительность
одного
канала, получим:
A=
*
;
=
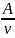 =
=
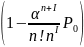
и
так как
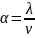 ,
то
,
то
=
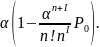
Средняя
длина очереди-
это математическое ожидание
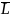 случайной величины L,
равной длине очереди или числу требований
в очереди. Очевидно, случайная величина
L
имеет следующий закон распределения:
случайной величины L,
равной длине очереди или числу требований
в очереди. Очевидно, случайная величина
L
имеет следующий закон распределения:
L: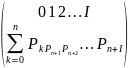 ,
,
Следовательно:
=
М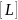 =
Pn+1+
2Pn+2
… Pn+I
=
Pn+1+
2Pn+2
… Pn+I
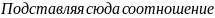 Pn+s=P0
(
S,
(S = 1,…, I) получим:
Pn+s=P0
(
S,
(S = 1,…, I) получим:
=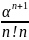 P0+
P0+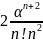 P0+…+I
P0=
P0+…+I
P0=
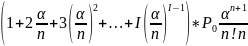 =
P0
=
P0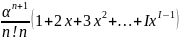 ,
,
где
обозначено X=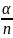 .
Выражение, стоящее в скобках, обозначим
через S
и рассмотрим два случая:
.
Выражение, стоящее в скобках, обозначим
через S
и рассмотрим два случая:
=n,
тогда
S=1+2+3+…+I=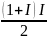 ;
;
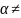 n,
тогда
S=1+2x+3x2+…+IxI-1=
n,
тогда
S=1+2x+3x2+…+IxI-1=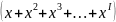 ’=
’=
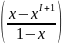 ’=
’=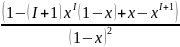 =
=
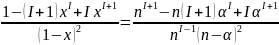
Окончательно имеем:
=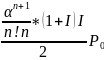 ,
,
 ,
,
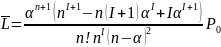 ,
,
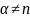
Среднее
число требований, находящихся в системе,
которое
обозначим
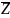 ,
складывается из среднего числа
обслуживаемых заявок
и средней длины
,
то есть:
,
складывается из среднего числа
обслуживаемых заявок
и средней длины
,
то есть:
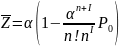 +
+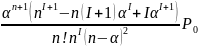 .
.
Среднее
время ожидания в очереди через
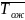 .
Если заявка стоит в очереди, то все
каналы обслуживания заняты, и случайное
время ожидания Тож
равно: для первой заявки из очереди
.
Если заявка стоит в очереди, то все
каналы обслуживания заняты, и случайное
время ожидания Тож
равно: для первой заявки из очереди
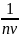 для второй заявки из очереди
для второй заявки из очереди
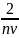 и т.д.
и т.д.
Поэтому Тож имеет следующий ряд распределения:
Тож: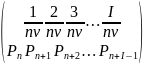 ,
,
Откуда
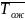 =М
=М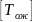 =
=
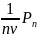 +
+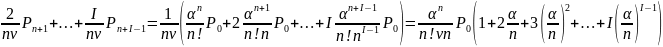 .
.
Просуммировав выражение в скобках так же, как и при выводе формулы
= , , получим:
=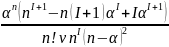 .
.
Из = , и = легко видеть, что
=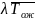 .
.
