49. Интервальные оценки параметров распределения

Два распределения, связанные с нормальным распределением.

Введем 2 утверждения:

1. Если СВ ξ₁, ξ₂, … ξ_n независимы и нормальны с параметрами (0, 1), то СВ Х² (хи квадрат) = ξ₁²+ ξ₂²+…+ ξ_n² имеет распределение, плотность которого дается формулой n/2>1

Р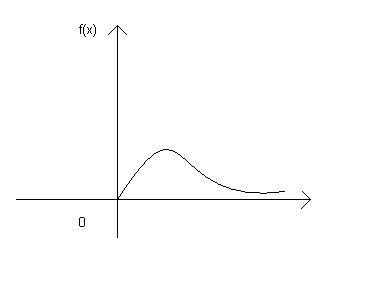 аспределение Х² или распределение Пирсона

2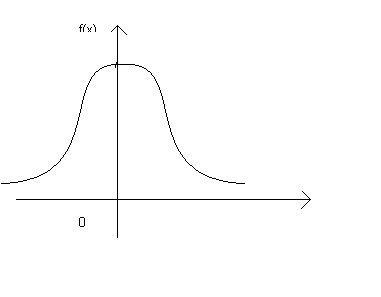 . Если СВ ξ₁, ξ₂, … ξ_n независимы и нормальны с параметрами (0, 1), то СВ имеет распределение, плотность вероятности которого дается формулой

Распределение Стьюдента

Квантиль распределения.

Пусть с испытание связана СВ ξ с функцией распределения F(x). Предположим, что F(x) монотонна и непрерывна (график)

Квантилем уровня Р называется корень уравнения F(x)=Р. Обозначим этот корень через Х_р Из определения функции распределения вытекает: F(Х_р)=P(ξ <Х_р)=P Далее у нас будут использованы квантили распределения Х² Пирсона и распределения Стьюдента.

Они обозначаются: Х²_р(n) – квантиль распределения Пирсона уровня Р с n-степенями свободы.

t_p(n) - квантиль распределения Стьюдента с n-степенями свободы.

Для этих квантилей составлены таблицы

Доверительные интервалы для мат.ожидания и дисперсии.

Пусть с испытанием связана СВ ξ с неизвестными параметрами (а; Д) и пусть по выборке найдены оценки этих параметров и S² Зададимся некоторым числом р (0;1). Тогда справедливо следующее утверждение: Теорема. В указанной ситуации при достаточно большом объеме выборки с вероятность Р выполняются следующие неравенства:

n – объем выборки

- квантиль распределения Стьюдента

- квантиль распределения Пирсона

Построенные интервалы называются доверительными интервалами с уровнем доверия Р

18.Биномиальный закон распределения вероятности

Обычно нас интересует лишь общее число успехов, достигнутых в последовательности из n испытаний Бернулли, а не порядок следования успехов. В этом смысле мы не делаем различий между событиями, состоящими, например, из последовательностей и т.д.

Событие “n испытаний привели m раз к успеху” содержит столько элементарных событий, сколькими способами можно распределить m символов по n местам, что совпадает с числом сочетаний из n элементов по m. Другими словами, пространство элементарных событий состоит из точек, каждая из которых, по определению, имеет вероятность .

Следовательно, вероятность m успехов (_­­­ ) в серии из n испытаний Бернулли описывается формулой

где p – вероятность успеха; q – вероятность неудачи в одном испытании (q = 1 – р).

Согласно существующей терминологии, число успехов в серии из n испытаний является случайной величиной, а формула (*) описывает распределение этой случайной величины и называется биномиальным законом распределения вероятности.Заметим, что выражение представляет собой m-ый член биномиального разложения .

Следовательно,

как того и требует понятие вероятности.Выражение, содержащее произведение вида представляет собой вероятность m успехов в серии из n испытаний Бернулли:

Заметим, что события

– 0 успехов,

– 1 успех,

– 2 успеха,

– …

– n успехов в серии из n испытаний Бернулли

образуют полную группу событий, поскольку они попарно несовместимы и вместе образуют достоверное событие.

Частные случаи.

– Вероятность того, что в серии из n испытаний успех не наступит ни разу, равна .

– Вероятность наступления хотя бы одного успеха в серии из n испытаний равна