13. Дисперсия и ско, свойства

Пусть с испытанием связана дисперсия СВ x, закон распределения который имеет вид:

x: + …..+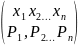

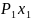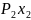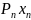
Рассмотрим два СВ:

x- 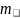- отклонения значения СВ от своего мат.ожидания

-Квадрат отклонения значения СВ от мат.ожидания

=

D[x]=M[ ]= + +

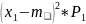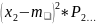Среднеквадратичное отклонения (СКО)-

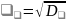Помнить: Дисперсия характеризует меру разброса значения СВ около своего центра с учетом возможности значений и вероятности этих значений.

Свойства:

1 D[а]=0

2 D[аx]= D[x]

3 D[x-h]=D[x]₊D[h], если x,i статистически независимые СВ

4 D[x]=М[ ]-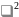

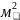
Док-во:

1. а:[ ]

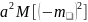2. D[x]=M[ ], D[ax]=M[ ]= M[ = = D[x]

3

Равно 0

. D[x-h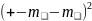]=M[ ]= M[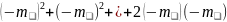 ]= M[ ]= M[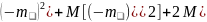 ]=D[x]+D[h]

0

4.D[x]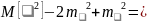=М[ ]- М[ ]-

Замечание:

Мы видим D[a]=0, дисперсия неслучайно равно 0, верно и обратное, если дисперсия равна 0, то величина явл. неслучайной,т.е. дисперсия явл. мерой случайной величины.

14. Плотность вероятности непрерывной св

П усть с испытанием связано непрерывное СВ x х

х х+Dх

Плотность распределения непрерывно СВx, называется пределом отношения вероятности попадания в отрезок [x, x+Dx] к длине отрезка Dх при условии, что отрезок стягивается к точке х:

Свойства:

1. F(x)≥0

2. P(xÎ(a,b)= 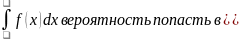a,b)- площадь заштрихованной фигуры

3. Площадь бесконечной фигуры, ограниченной сверху

, снизу осью Ох.

Док-во:

1.Первое свойство вытекает из того, что предел неотрицательной функции неотрицателен.

2. =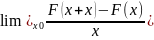 =F’(x), f(x)=F’(x)

3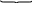 .S=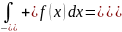 P(xÎ(-¥;+¥))=1

0

Плотность распределения f(x), показывает как 100% вероятность распределена между возможными интервалами.

Замечание : если отрезок [0;1] заменить отрезком [а;в], то ОВ=x у которого все значения на отрезке [а;в] равновозможны, а в не отрезка невозможны, называется равномернораспределенной на отрезке [а;в].

0 x≤a

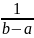f (x)= a≤x≤b

0 x>b

S=(b-a)*h=1

h=

15.Функция распределения случайной величины.

П усть с испытанием связана непрерывная СВ x, зафиксируем на числовой оси некоторое число х. Тогда результатом испытания может быть 3 исхода: x>х, x=х, x<х.

x

Все 3 исхода случайны и ,следовательно, можно говорить об их вероятности обозначения через F(x) вероятность x<х и называется функцией распределения.

С войства: у

1. 0≤ F(x)≤1

2. F(x) неубывающая функция 1

3. F(-¥)=0; F(+¥)=1

4. P(xÎ(a,b)=

0 х

Док-во:

1. Первое свойсво вытекает из определения вероятности, т.к. 0≤ Р≤1

2. Вытекает из того, что при увел. Х. интервал (х;-¥) расширяется, следовательно, вероятность в него попасть не уменьшается.

3. F(-¥)=P(x=-¥)=0

F(-¥≤x≤+¥)=P(x<+¥)=P(-¥≤x≤+¥)=1

0

4. F(b)=P(x<b)=P(x<a+x=a+xÎ(a;b))=P(x<a+x(x=a)+P(xÎ(a;b)))=F(a)+0+ P(xÎ(a;b))=F(b)-F(a)