1.Классическое определение вероятности

Пусть с испытанием связано интересующее нас событие А- случайное, если оно может появиться в результате испытания а может и не появиться. Оно называется достоверным если обязательно появится в результате испытания и невозможным если обязательно не появится в результат испытания. Определение: Пусть испытание имеет n-равновозможных исходов из которых интересующему нас событию А благоприятствуют m исходов. Тогда вероятностью события А при данном испытании называется отношение числа благоприятных исходов к числу всех равновозможных исходов и обозначается: P(A)=m/n

2.Геометрическое определение вероятности

Испытание: равновозможным способом берем точку из области Д; Событие А- попадание в d; Р(А)-? Классическое определение здесь не подходит. Т.к. Р(А)=площадь d / площадь Д = благоприятная площадь / вся возможная площадь. Действия над событиями: пусть с испытанием связано 2 события А,В. Определения: 1)Сумма событий А,В называют событие С, состоящее в появлении хотя бы 1 из событий А или В и обозначаются: С=А+В

2) Произведение событий А,В называют событие С, состоящее в одновременном появлении событий А,В и обознач: С=А*В; 3) Событие В называют противоположным событию А, если оно состоит в не наступлении события А и обознач: В=А (с чертой вверху)

5.Условная вероятность. Теорема умножения вероятностей.

Пусть с испытанием связаны события А,В. Запись Р(В/А) означает: вероятность события В при условии, что событие А наступило. ПРИМЕР: Испытание: берут наугад точку в области Д равновозможным образом. А-попадание в d1,

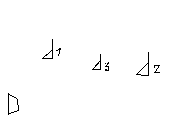В-попадание в d2. тогда имеем Р(В)=пл.d2/ пл.Д , Р(В/А)=благоприятная площадь/вся возможная площадь = пл.d3/пл.d1; Вероятность Р(В/А) называется условной вероятностью. Теорема: Р(А*В)=Р(А)*Р(В/А),т.е. вероятность произведения двух событий = произведению вероятности первого события на вероятность другого при условии, что первое произошло. Доказательство: Испытание: (смотри выше) Р( А*В)=пл.d3/пл.Д = пл.d3*пл.d1/пл.Д*пл.d1=Р(А) *Р(В/А) Замечания:1)События А,В называются независимыми, если Р(В/А)=Р(В),т.е. Р(В) не зависит от того наступило событие А или нет. Для независимых событий Р(А*В)=Р(А)*Р(В),т.е. вероятность произведения независимых событий = произведению вероятностей этих событий.;2) Р(А*В*С*Д)=Р(А)*Р(В/А)*Р(С/А*В)…

10.Случайные величины. Статистически зависимые и независимые с.в.

Пусть с испытанием связано число, зависящее от случая. Будем называть это число случайной величиной:ƺ(сигма) ƞ(ню).Пример С.В:1)Число успехов в серии n независимых испытаний;2)Число знаков поступающих на АТС за определенный промежуток времени;3)Продолжительность телефонного разговора;4)Результат измерения некоторой величины с помощью прибора. СВ называют дискретной если она принимает отдельные изолированные значения и непрерывной если ее значения сплошь заполняют некоторый отрезок или всю числовую ось. В теории вероятности изучается слабая зависимость между величинами, когда значению одной величины отвечает целый разброс значений другой величины. Пусть с испытанием связаны 2 с.в. ƺ и ƞ. Если для любой пары чисел а,в выполняется равенство Р(ƺ<а/ ƞ<в)=Р(ƺ<а);если она не выполняется хотя бы для одной пары чисел, то ƺ статистически зависит от ƞ. Реальный смысл статистической зависимости состоит в следующем: если любая инфо.о значениях 1с.в.не дает возможность высказать какие-либо суждения о значениях др.с.в., то такие с.в. являются статистически независимыми. Р(А/В)=Р(А)- событие А не зависит от Р(В) из этого следует с.в. ƺ не зависит от с.в. ƞ, если для любых а,в выполняется равенство Р(ƺ<а/ ƞ<в)=Р(ƺ<а),т.е. Р(ƺ<а) не зависит от Р(ƞ<в) для любых а,в.