2.2. Измерительные схемы датчиков

.Вариации импеданса Z_д ЧЭ, связанные с изменениями измеряемой величины x, могут быть преобразованы в электрический сигнал путем включения ЧЭ в измерительную схему, питаемую источником напряжения E или тока I. Измерительные схемы, назы­ваемые так­же схемами формирования сигналов, пред­назна­чены для преобразования ин­фор­ма­ции, полученной ЧЭ в процессе измерения в электриче­ский сигнал (в фор­ме ва­риа­ций амплитуды, фазы или частоты).

Наиболее распространены два типа измерительных схем датчиков: параметрические и генераторные.

В первом случае, функция преобразования измерительной схемы описывается вы­ра­жением вида:

U_выx = f(x) = E F (Z_д, Z_с )

Во втором: w_выx (x) = G(Z_д, Z_с),

Здесь Z_с - собственный импеданс измерительной схемы, E - напряжение питания, w_выx - частота выходного сигнала.

Потенциометрическая схема (рис. 2.25) в измерительных цепях датчиков используется наиболее часто. ЧЭ Z_д включается последовательно с дополнительным элементом Z_с, образуя делитель напряжения. Главным достоинством потенциометрической схемы является простота, главным недостатком - чувствительность к паразитным помехам.

В мостовой схеме, являющейся модификацией потенциометрической и содержащей два дифференциально включенных делителя, удается су­щественно снизить вли­я­ние вне­ш­них факторов.

Чувствительность датчика S_д, использующего измерительные схемы этого типа определяется выражением:

S_д = DU_выx/Dx = (DU_выx/DZ_д)´( DZ_д/Dx) = S_с S

где DU_выx/DZ_д = S_с - чувствительность измерительной схемы, DZ_д/Dx = S - чувствительность ЧЭ.

В генераторных схемах (рис. 2.26), вариации импеданса ЧЭ вызывают изменение частоты генерации. В этом случае, выходной сигнал является частотно-моду­лированным. Такая схема обеспечивает хорошую защиту от паразит­ных влияний, особенно в случае использования длинных линий связи. Чувствительность генераторной схемы S_с = Dw_выx/DZ_д и тогда, также как и в предыдущем случае, получим:

S_д = Dw_выx/Dх = S_с S

Функция преобразования датчика будет линейна, если чувствительность измерительной схемы S_с не зависит от х.

2.2.1. Параметрические схемы

В параметрических схемах осуществляется преобразование импеданса ЧЭ или группы ЧЭ в электрический сигнал в форме напряжения или тока. Параметрическая схема может состоять исключительно из ЧЭ или включать наряду с ними и дополнительные элементы, корректирующие ее функцию преобразования. Среди всех параметрических схем наибольшее применение нашли потенциометрические и мостовые измерительные схемы.

Рассмотрим классическую потенциометрическую схему с резистивными эле­ментами. ЧЭ R_д включен последовательно с резистором постоянного сопротивления R₁ (рис. 2.27). Питание осуществляется от источника ЭДС E с внутренним сопротивлением R.

Выходное напряжение схемы U_вых, измеряемое при­бором с собственным сопро­тив­лением R_н (измерительный усилитель, вольтметр) будет равно:

Общепринятым требованием при построении измерительных схем является условие R_н>>R_д. В этом случае, напряжение U_вых не зависит от нагрузки и является нелинейной функцией:

В большинстве случаев требуется, чтобы вариации напряжения U_выx были пропорциональны вариациям сопротивлений ЧЭ R_д. Ли­­неаризация потенциометрических схем дос­тигается двумя основными способами: работой в малой (линейной) зоне и использованием дифференциального включения ЧЭ.

Работа в малой зоне предполагает, что сопротивление ЧЭ меняется от R_д0 до (R_д0 + DR_д) вызывая изменения напряжения U_выx от U_выx0 до (U_выx0 + DU_выx). Опуская промежуточные выкладки, получим:

При условии, что DR_д << R_д0 + R₁ + R с точностью до малых величин второго порядка имеем 

Чувствительность измерительной схемы S_с = DU_выx/DR_д максимальна, если выбрать  R + R₁ = R_д0;  в этом случае функция преобразования будет равна:

Дифференциальное включение образуется заменой постоянного сопротивления R₁  вто­­­­­рым ЧЭ, идентичным первому, но с вариациями номинала обратного знака R₁= R_д0 - DR_д. Тогда при включении этих двух ЧЭ навстречу друг другу получим  так называемую двухтактную схему. (Это могут быть, например, два оди­наковых ТР, подвергаю­щих­ся равным по величине, но противоположным по знаку деформациям).

Тогда 

откуда функция преобразования

Дифференциальное вклю­чение ЧЭ позволяет скомпенсировать влияние многих факторов. Рассмотрим потенциометрическую схему с двумя ЧЭ R_д1 и R_д2, вариации которых вызывают соответствующие приращения DU_выx1 и DU_выx2 измеряемой величины (рис. 2.28). Обозначено g  - вели­чина вли­яющего фактора, а  Dg - ее приращение, одинаковое для двух ЧЭ.

До воздействия измеряемой величины имеем

x₁ = x₂,  g = g₀, R_д1 = R_д2 = R_д0, U_выx = U_выx0 =E/2

После воздействия измеряемой величины

R_д1 = R_д0 +DR_д1, R_д2 = R_д0 +DR_д2,

где DR_д1 = S_g Dg + S Dx₁, DR_д2 = S_g Dg + S Dx₂

Здесь S_g = DR_д/Dg - чувствительность каждого ЧЭ к вли­яющему фактору,  S =DR_д/Dx - их чувстви­тель­ность к измеряемой величине. Выходное напря­жение равно U_выx(x) = U_выx0 +DU_выx. Пола­гая  R << R_д0 получим:

Если первый из ЧЭ не подвергается воздействию измеряемой величины ( Dx₁ = 0), то

при условии, что  S Dx₂ << R_д0

При совместных измерениях, когда   Dx = Dx₂ = - Dx₁, имеем:

Следовательно, при дифференциальном включении влияющие факторы в функции преобразования представлены намного слабее, чем измеряемая величина.

Недостатком потенциометрической схемы является наличие в выходном сигнале постоянной соста­вляющей, не содержащей полезной информации. Для выделения полезной DU_выx составляющей сигнала можно использовать емкостную связь меж­ду схемой и нагрузкой (рис. 2.27). В этом случае, конденсатор C и внутреннее сопротивле­ние R_н образуют фильтр верх­них частот.

Для устранения постоянной составляющей используют также потенциометрическую схему с симметричным питанием или мостовую схему.

Мостовая схема представляет собой двойной потенциометр с дифференциальным включением. Ее основное преимущество заключается в большей точности и меньшей чувствительности к влияющим факторам, чем у потенциомет­ри­ческой схемы.

В зависимости от типа ЧЭ мостовые схемы получили собственные имена: мост Вина, мост Саути, мост Максвелла и др. (Два первых представлены на рис. 2.29). Наиболее известна резистивная мостовая схема Уитстона (рис. 2.30). Нагрузка R_н включается в диагональ моста. Мост находится в равновесии, когда напряжения в точках a и b равны  u_a= u_b, т.е. i_ab = 0. Это условие достигается известным соотношением:

R₁ R₄ = R₂ R₃

Условие равновесия зависит только от сопротивления плеч моста, оно не зависит от внутреннего сопротивления источника питания R и сопротивления нагрузки R_н.

Обычно мост питают источником, внутреннее сопротивление которого мало: R << R₁, R₂, R₃, R₄, R_н. В идеальном случае  R = 0 выражение для  тока i_ab имеет вид [ ]:

Когда нагрузка (осцил­лограф, вольтметр или усилитель) имеет большое входное сопротивление R_н >> R₁, R₂, R₃, R₄, получим:

и

Зависимость U_вых = f(R) описывает функцию преобразования мостовой схемы Уитстона. Чувствительность моста S_и максимальна в положении равновесия, когда  R₁ = R₂ и R₃ =  R₄. Для упрощения процедуры измерений часто выбирают сопротивления плеч моста одинаковыми: R₁ = R₂ = R₃ = R₄ = R₀.

В общем случае, в мосте может быть одно-, два- и четыре рабочих плеча. Для схемы с четырьмя рабочими плечами (т.е. в каждое плечо включен ЧЭ) их вариации равны соответственно:

R₁ = R₀ + DR₁, R₂ = R₀ + DR₂, R₃ = R₀ + DR₃,  R₄ = R₀ + DR₄

Тогда, напряжение разбаланса будет определяться соответствующей подстановкой значений R₁, R₂, R₃, R₄ в выражение для функции преобразования. Существенно, что это напряжение является нелинейной функцией вызвавших его изменений сопротивлений плеч моста. Так, если в схеме используется только один ЧЭ, например, R₂, то

На рис. 2.31 представлена зависимость отно­шения U_вых/E от  изменения одного из плеч DR/R₀ моста, изначально находившегося в равновесии [ ]. Эта зависимость линейна в относительно узком диапазоне из­менения R₀ в обе стороны от положения равновесия. На практике ограничиваются |DR/R₀| £ 0,1. Когда со­­про­тивление источника R того же порядка, что и сопротивления плеч моста, а  R_н намного больше, напряжение разбаланса можно выразить формулой

При прочих равных условиях увеличение чувствительности S_и мостовой схемы требует снижения сопротивления источника R.

Улучшение функции преобразования мостовой схемы заключается в линеаризации характеристики и компенсации влия­ющих факторов. Так же как и в потенциометрических схемах наиболее известны два способа: работа на малом участке характеристики и дифференциальное включение ЧЭ.

В первом случае, мост из четырех одинаковых ЧЭ R₀, вариации которых DR_i малы (DR_i << R₀) с точностью до величины второго  порядка  линеен близ положения равновесия:

Это соотношение отражает очень важное свойство моста, у которого все плечи в положении равновесия одинаковы: идентичные изменения сопротивлений в двух смежных плечах не приводят к разбалансу моста. Данное свой­­ство позволяет компенсировать воздействия вли­яющих факторов, в том числе температурных изменений.

При дифференциальном включении плечи моста образованы из четырех одинаковых ЧЭ, изменения номи­налов ко­торых в смеж­ных плечах попарно противоположны, т. е:

DR₁ = - DR₂ и DR₃ = - DR₄

Тогда, при линейных ЧЭ напряжение разбаланса будет строго линейно зависеть от изменений этих сопротивлений: 

и при  DR₂ = DR₃ = DR получим функцию преобразования в виде:

Если же ЧЭ имеют нелинейные характеристики, то их дифференциальное включение в мостовую схему уже не обеспечит строгой линейности функции преобразования. В этом случае часто говорят о квазилинейности этой функции, что вполне достаточно для инженерных расчетов. Однако такая схема не обеспечит полной компенсации влияющих факторов. Так, для схемы мо­с­­та с четырьмя идентичными ЧЭ имеем

DR₁ = - SDx + S_g Dg,  DR₂ = S Dx + S_gDg, DR₃ = SDx + S_g Dg,  DR₄ = - S Dx + S_gDg

и общее выражение для U_вых  приво­дится к виду

Видно, что напряжение U_вых  пропорционально изменениям только измеряемой величины, но чувствительность схемы  S_д = U_вых/Dx зависит от вли­я­ющей  величины g  из-за  непостоянства чувствительности S_g дат­чика при воз­де­йствии величины  g.

Чаще всего влияющим фактором является температура Т. Ее вариации Dg = DТ =Т - Т₀, где Т₀ - значение температуры при равновесии моста, когда сопротивление каждого ЧЭ равно R₀. Чувствительность S_g = DR/DТ = a_RR₀, a_R - температурный коэффициент сопротивления ЧЭ. В этом случае напряжение разбаланса

Линеаризовать функцию преобразования в этом случае можно, включив последовательно с источником питания температурно-зависимые резисторы с сопротивлением  R/2 (рис. 3.32), вариации которых с тем­пературой из­меняют напряжение питания U  моста таким образом, что чувствительность всей схемы остается постоянной. Так, если в диапазоне температур, в которых используется схема, тепловые вариации вызывают квазилинейные изменения сопротивлений схемы и источника вида: R_д(T) = R_д0 (1 + a_R DT) и S(T) = S₀ (1 + b DT)

то, напряжение  U_вых не зависит от  Т, если для сопротивления источника R справедлива зависимость

здесь a_R и a - температурные коэффициенты сопротивлений (ТКС) ЧЭ и источника, b - температурный коэффициент чувствительности (ТКЧ) ЧЭ.

Номинальные значения ЧЭ во всех плечах моста, так же, как их температурные коэффициенты, никогда не оказываются строго идентичными. Поэтому, даже в отсутствие измеряемой величины, наблюдается отличное от нуля напряжение разбаланса, изменяющееся в фун­кции температуры. Это напряжение называется сдвигом (или дрейфом) нуля. Оно образует ад­дитивную погрешность, входящую в результат измерения.

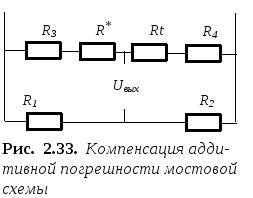
Коррекция дрейфа нуля осуществляется включе­нием в смежные плечи моста двух резисторов: R_t и  R^* (рис. 2.33). Сопротивление первого зависит от температуры, так, что знак изменения сопротивления противоположен знаку ЧЭ. Сопротивление второго не зависит от температуры и служит для начального симметрирования моста.