3.1.3.2. Кодовые оптические датчики положения

Рассмотренные ранее ДПП формируют выходной сигнал либо в аналоговом виде, либо, как ИОДП, в виде последовательности импульсов. Однако в большинстве случаев ДПП являются элементами цифровых систем управления, что требует преобразования выходного сигнала в цифровую форму. Именно такой сигнал формируется в кодовых фотоэлектрических датчиках (КОДП). Оптические системы КОДП и ИОДП построены похожим образом, а кодирующая шкала КОДП пред­ставляет собой стеклянное основание с нанесенной на ней кодовой маской. Маска выполнена в виде нескольких (обычно до 20) дорожек с прозрачными и непрозрачными сегментами (рис. 3.41). Количество дорожек, как правило, определяет разрядность выходного двоичного кода. Осветитель создает лучистый поток, падающий на шкалу. В момент съема информации луч, проходя через прозрачные сегменты кодовых дорожек шкалы и ограничивающую щелевую диафрагму, освещает фо­то­приемники (фотодиодные линейки), усиленные сигналы с которых принимаются за двоичные единицы. Отсутствие сигнала с фотоприемника соответствует двоичному нулю. В результате каждому перемещению соответствует определенная комбинация двоичных единиц и нулей, являющаяся его цифровым кодом.

Как известно, произвольное целое число A можно представить в любой системе счисления с основанием B в виде ряда:

А = а_n Вⁿ + а_n-1 В^n-1 + ... + а₁ В¹ + а₀ В⁰ ,

здесь a_n , ... a₀ - коэффициенты разрядов, они могут принимать значения от 0 до (B-1). Наибольшее распространение в цифровой измерительной технике получила двоичная система счисления, где B = 2, и, следовательно, коэффициенты а_i могут принимать два значения:«0» и «1». В двоичной системе максимальное число А_max, которое мож­­­но закодировать при n разрядах, равно А_max = 2ⁿ - 1. Для КОДП угла разрешение шкалы составит 2p/2ⁿ . Следовательно, разрешающая способность КОДП D_a определяется числом разрядов n его кодовой шкалы. Связь разрешающей способности КОДП с разрядностью кодовой шкалы иллюстрирует табл. 3.13.

Таблица 3.13. Зависимость разрешающей способности от разрядности шкалы КОДП

Число разрядов шкалы, n	2	4	8	10	16
Разрешающая способность, Da	90о	22,5о	1о24’	21’5”	20”

Вид конструктивной схемы КОДП определяется, главным образом, числом раз­рядов шка­лы и способом кодирования и считывания. В КОДП, наи­более часто используются две схемы: КОДП с прямым двоичным кодом и КОДП с кодом Грея.

Шкалы с прямым двоичным кодом представля­ют собой оптические рейки или диски, разделенные на равновеликие площадки - полосы для реек и сектора - для дисков, на которых записаны бинарные слова, соответствующие прямому двоичному коду. Светлый элемент шкалы, пропускающий свет, переводит фотоэлементы в состояние «1». Темные участки шкалы соответствуют «0». Число площадок N определяет разрешающую способность КОДП: D_a = L/N или D_a = 360⁰/N . (Здесь L - длина рейки).

Несмотря на простоту кодирования и считывания шкалам с обычным двоичным кодом присущ крупный недостаток, связанный с появлением ложный кодов. Эта особенность обусловлена невозможностью изготовления идеальных шкал и проявляется во время движения шкалы, в момент изменения «1» на «0» или «0» на «1» одновременно в нескольких разрядах. Так, при изменении кода 15 на 16, т.е. 01111 на 10000 происходит замена значений сразу в пяти разрядах. Если же, случайно (из-за погрешностей шкалы), например, во 2 разряде, не происходит изменение «1» на «0», тогда вместо значения «16» будет считано «18» (10010). Существенно, что величина ошибки превышает цену деления шкалы, равную одному младшему значащему разряду (МЗР). Вероятность возник­новения неоднозначности считывания информации в КОДП особенно велика при высоких скоростях движения шкалы.

Для устранения неоднозначности считывания применяются специальные методы считывания и специальные коды.

Одним из таких методов является V-считы­вание, особен­но распространенное в контактных ДПП (рис. 3.42). Здесь сохраняется обычная двоичная шкала, но на каждой дорожке, кроме младшей используется по два приемника.

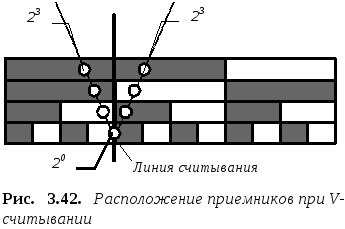Один приемник (условно называемый опережающим) устанавливается относительно опорной линии считывания чуть впереди, а другой (отстающий) - чуть сзади (рис. 3.42). Каждая пара таких фотоприемников подключается к отдельной логической схеме, обеспечивающей идентификацию истинного значения считываемого разряда (рис. 3.43). Считывание в МЗР осуществляется одним фотоприемником. Он установлен точно по опорной линии считывания. Расстояние между приемниками в других парах составляют 1x, 2x, 4x, 8x и т.д., где x - длина элементарного приращения (одного МЗР) в мм. МЗР изменяется на каждом шаге, поэтому сигнал с первой дорожки используется для управления приемниками следующей дорожки. Алгоритм работы логической схемы основан на анализе изменения состояния разрядных дорожек. Если двоичное число увеличивается, то при изменении МЗР от «0» к «1» другие разряды своего состояния не изменяют. Если же состояние МЗР меняется от «1» к «0», то должно изменяться состояние, по крайней мере, еще одного из разрядов. Данный алгоритм реализуется аппаратно с помощью схемы, представленной на рис.

В соответствии с алгоритмом, выходной сигнал для дорожки следующего по старшинству разряда считывается с запаздывающего приемника, если для двух из них на дорожке предыдущего разряда истинный выходной сигнал соответствует «1». Если же для данной дорожки истинным является выходной сигнал «0», то с дорожки следующего по старшинству разряда сигнал будет считываться с опережающего приемника. Синхронизация всех разрядов производится сигналом МЗР. Таким образом, логическая схема определяет, который из двух приемников каждой дорожки имеет истинный выходной сигнал.

Другой путь повышения надежности преобразования основан на применении циклического кода Грея, разработанного в Массачусетском технологическом институте, США в 1953 году. Большинство выпускаемых промышленно КОДП используют именно этот код, при ко­тором ошибка считывания не превышает величины МЗР, независимо от того, в каком из разрядов произошла ошибка. Иллюстрация этого обстоятельства приведена в табл. 3.14.

Недостатком датчиков, использующих шкалы с кодом Грея, является необходимость последующей дешифрации кодов Грея в стандартный двоичный код.

Обозначим некоторое число в двоичном коде как B = b_n b_n-1 ... b₂ b₁ , и его же в коде Грея как G = g_n g_n-1 ... g₂ g₁. Тогда, для преобразования его из двоичного кода в код Грея справедливо выражение:

g_k = b_k+1 Å b_k (mod 2)

Сложение по модулю 2 (нерав­нозначность) реализуется по следующему алгоритму: 1 + 1 = 0, 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1.

Таблица 3.14. Таблица перевода двоичных кодов

Десятичное число		Двоичный код		Код Грея
0 1 2 3 4 5 6 7 8	9 10 11 12 13 14 15 16	00000 00001 00010 00011 00100 00101 00110 00111 01000	01001 01010 01011 01100 01101 01110 01111 10000	00000 00001 00011 00010 00110 00111 00101 00100 01100	01101 01111 01110 01010 01011 01001 01000 11000

Промышленно выпускаются одношкальные и двухшкальные КОДП (с системой ГО и ТО). Самые современные датчики первого типа имеют 12 … 16 разрядную шкалу, двухшкальные КОДП содержат две 7… 9 разрядных шкалы. И та и другая схемы позволяют получить 16 разрядный двоичный код и гарантировать разрешающую способность до 20 ".

Некоторые модели КОДП представлены в табл. 3.15.

Таблица 3.15. Примеры промышленных КОДП

Модель	n, разряд	K , шкал	N, об	Da, ‘	w, об/мин	Æ, мм	l, мм	m, кг
ППК-15	15	2	16	10,5	900	50	160	0,8
ROC 717	17	1		0,2				0,6
TSI-200	20	2		0,5		70	75	0,4

Примечание.

1. Датчики ROC и TSI-200 изготовлены фирмами Heidenhain, Германия и Tama­gawa, Япония.

2. Датчики ROC используются в системах уп­равления солнечными батареями и антен­на­ми радиостанций.

В настоящее время все самые современные системы измерения перемещений строятся на основе КОДП. Их достоинства связаны с возможностью непосредственного получения двоичного кода и высокой точностью измерений. Недостатки этих датчиков обусловлены технологической сложностью и высокой стоимостью, а также значительными габаритами.