6.6.1. Предварительная обработка изображений

Все методы предварительной обработки изображений можно подразделить на пространственные и час­тот­ные.

Пространственные методы обработки являются процедурами, оперирующими непосредственно с пикселями изображения. В общем виде, функции предварительной обработки в пространственной области записываются в виде выражения:

где F (x, y) и G (x, y) - соответственно изображение на входе и выходе преобразователя, H – оператор (функция преобразования). В качестве характеристики изображения используется яркость L(x, y).

Частотные методы обработки связаны с переводом изображения в комплексную плоскость с помощью преобразования Фурье.

Первый этап предварительной обработки представляет собой формирование изображения. Формированием изображения называется процедура непосредственного получения изображения в виде массива дискретных элементов - пикселей, образующих матрицу или контур и расположенного в памяти видеопроцессора. Пример изображения некоторого (тестового) объекта G(x, y) представлен на рис. 6.43.

На этапе формирования изображения в СТЗ производится его фильтрация, т.е. аппаратная или программная компенсация оптических помех и сглаживание дискретного изображения, а также выделение контуров - краев и линий. (Как уже отмечалось во введении, до 90% всей информации об изображении содержится в его контуре).

Основные этапы формирования изображений приведены в табл. 6.18.

Таблица 6.18. Этапы формирования изображений

Формирование изображений
1	Выбор порога яркости (улучшение)
2	Фильтрация	Компенсация помех Сглаживание
3	Выделение контуров
4	Бинаризация

Преобразование цифрового изображения L(m, n) на этапе выделения контуров значительно уменьшает объем визуальной информации - обычно передаются только координаты и яркость элементов, относящихся к границам перепадов яркости. Величина этого перепада задается относительно некоторого значения яркости, называемого порогом.

Рассмотрим некоторые особенностивыбора порога яркости. Качество изображения в СТЗ сильно зависит от освещенности рабочей сцены. Если она занижена, то увеличивается количество помех на изображении (вплоть до потери объекта), при очень сильной освещенности происходит засветка изображения (и опять же потеря объекта). В современных СТЗ предусмотрены средства автоматической адаптации при изменении освещения, получившие название систем автоматической регулировки освещения. Использование этих средств позволяет компенсировать некоторые помехи, в частности, блики и тени.

Наиболее известный способ улучшения изображения пред­полагает программную (покадро­вую) регулировку яркости и контрастности вводимого изображения. Для каждого кадра строится гистограмма распределения яркости изображения L(x, y) (рис. 6.44), и вычис­ляются ее параметры: ма­тематическое ожидание (среднее значение) и ди­с­­персия. На рисунке обозначено n - количество пикселей L(x, y) - яркость.

Каждая точка гистограммы определяет, какое количество пикселей на изображении имеет данное значение яркости. При этом среднее значение гистограммы определяетобщую яркость изображения, а дисперсия (размах гистограммы) - его контрастность. Иногда вместо гистограммы распределения яркости используется функция плотности вероятности P(L_n) нормированного значения яркости L_n [0,1] (рис. 6.45).

Обычно перед началом работы производится настройка уровня освещенности по гистограмме изображения. Данная процедура является рекуррентной. Вычисленные параметры гистограммы распределения яркости текущего кадра сравниваются с оптимальными - определенными заранее экспериментальным путем; после чего соответствующим образом изменяются значения регистров фреймграббера. Затем считывается следующий кадр, снова строится гистограмма, вычисляются ее параметры и т.д. Так продолжается до тех пор, пока отклонение текущего среднего значения и дисперсии от оптимума не становится меньше некоторой заранее заданной величины (например,10 %). В этом случае, наст­ройка заканчивает­ся, и управление передается основной части программы.

Коррекция гистограммы дает общее улучшение качества на всем поле изображения. Для улучшения изображения малых участков указанный подход применяют к некоторой окрестности изображения. Тогда, для каждого пикселя строится гистограмма точек данной окрестности, которая используется для отображения яркости пикселя, расположенного в центре выбранной окрестности. Далее центр перемещается на соседний пик­­сель, и вся процедура повторяется снова.

Процедура бинаризации, т.е. преобразования полутонового изображения в бинарное, может проводиться непосредственно после гистограммного улучшения с помощью гистограммы полутонов. Так, если в изображении представлены светлые объекты на темном фоне гистограмма будет двухмодальной - яркости пикселей объектов и фона образуют две области. Бинаризованное изображение тестового объекта приведено на рис. 6.46. Для отделения объекта от фона выбирается пороговое значение яркости L_пор, которое разделяет эти области. Любая точка изображения с яркостьюL(x, y) > L_пор принадлежит объекту, а в противном случае - фону. Выходное бинаризованное изображение D(x, y) содержит лишь две градации яркости: 0 или 1, причем:

Таким образом, на изображении D(x, y) пиксели со значением 1 принадлежат объектам, а пиксели со значением 0 - фону.

Фильтрация изображения является, пожалуй, наиболее длительной и сложной стадией предобработки. На данный момент, в мире существует огромное количество различных способов фильтрации и у каждого есть свои достоинства и свои недостатки. В общем случае, фильтрация решает следующие основные задачи:

• «сглаживание» или подавление высокочастотной помехи (типа «снег»);

• повышение контрастности;

• выделение контура.

Как известно, на начальных этапах преобразования на изображение действуют аппаратурные помехи, искажающие функцию распределения интенсивности света L(x, y). (Сюда относятся искажения, вносимые оптикой, дискретизацией по полю из-за отдельного расположения ячеек светочувствительной поверхности и неоднородностью их фотоэлектрических характеристик и т.д.). Фильтрация помех - сгла­живание чаще всего проводится после получения цифрового изображения, и смысл ее заключается в усреднении (по определенному правилу) значения функции L(m, n) внутри небольшого анализируемого фрагмента (программ­ного окна), сканирующего изображение.

Обычно спектр визуальных помех содержит более высокие пространственные частоты, чем спектр изображения. Для их устранения используетсяфильтр нижних частот, подавляющий высокие частоты (при этом ухудшается резкость изображения).

В отличие от него, фильтр верхних частот оставляет без из­менения высокие частоты и сглаживает области, содержащие мало деталей. Примеры высоко и низкочастотной фильтраций тестового объекта показаны на рис. 6.47.

В большинстве случаев, сгла­живающие фильтры апроксимируются выраже­ниями вида:

Данная запись означает, что пикселю с номером (m, n) присваивается значение «1», если соседние пиксели, лежащие в некотором программном окне, принадлежат изображению объекта A.

Большинство фильтров используют методы пространственной области, т.к. оперируют с некоторой окрестностью точки. Данная окрестность называется апертурой фильтра и бывает, как правило, квадратной или прямоугольной формы (рис. 6.48). Используются также и другие апертуры, например круг, крест и пр. Однако квадратная апертура является наиболее предпочтительной из-за простоты ее реализации. Размер программного окна, как правило, составляет (33) или (55) пикселей.

Если в функции фильтра значение центрального пикселя апертуры не учитывается, то такая апертура называется выколотой.

Обычно, фильтрация изображения осуществляется путем последовательного (построчного) сканирования апе­ртурой выбранного фильтра. При достижении конца строки центр апертуры перемещается на начало новой, и все повторяется до тех пор, пока не будет достигнут конец массива.

Степень сглаживания изображения целиком определяется апертурой фильтра. Чем больше размер апертуры, тем выше степень сглаживания изображения. Однако с увеличением размерности апертуры N растет и время обработки - пропорционально N².

Среди линейных методов фильтрации наибольшее распространение получили методы порогового сглаживания, анизотропной и рекуррентной фильтрации.

Метод порогового сглаживания является одним из простейших. Он основан на сканирова­нии цифрового изображения программным окном (апертурой) размерностью NN (N = 3, 5 или 7) и вычислении на каждом шаге значения средней яркости L_ср группы элементов:

,

здесь l_ij - элементы функции яркости L(m, n), N - количество пикселей в окрестности точки (m, n).

Далее, значение средней яркости L_ср сравнивается со значением яркости центрального элемента сканирующего окна l_ij, и в случае, если l_ij > L_ср+_L, где _L - заданное пороговое значение, то вместо l_ij анализируемому элементу приписывается значение L_ср.

Так, при сканировании массива изображения квадратной апертурой размерностью 33, яркость центрального пикселя изображения (точку e) можно определить из выражения:

Часто используется выколотая квадратная апе­р­тура размерностью 33 (это связано с тем, что деление на 8 можно осуществить путем сдвига двоичного числа на три позиции, что гораздо быстрее, чем выполнять деление на 9):

Сущность анизотропной фильтрации заключается в свертке исходного массива изображения L(m, n) размерности IJ и сглаживающего массива W(m, n) размерности NN (N < I, J). Как и при пороговом сглаживании N = 3, 5 или 7.

Элементы «сглаженного» массива B(m, n) вычисляются согласно выражению:

При анизотропной фильтрации величина интенсивности каждого пикселя умножается на соответствующий вес этого пикселя. Так, если по каким-либо основаниям полагают, что пиксели, занимающие левое верхнее положение в апертуре фильтра должны иметь наибольший вес, то формула изменится следующим образом:

Для обработки краевых элементов кадра, к нему программно добавляются нулевые строки и столбцы. Сглаживающий массив нормируется, так, чтобы при фильтрации не изменялась средняя яркость изображения.

Наиболее распространены сглаживающие массивы W(m, n) следующих видов:

Аналогичный принцип положен в основу метода рекуррентной фильтрации, однако, здесь исполь­зуются не только элементы исходного массива L(m, n), но и элементы уже «сглаженного» массива B(m, n). Поэлементные операции проводятся согласно выражению

,

здесь элементы l_ij берутся сначала из исходного массива L(m, n), а затем из массива B(m, n).

Особенностью рекуррентной фильтрации является экономия памяти СТЗ, т.к. нет необходимости в сохранении исходного массива. Новые значения яркости пикселей, вычисленные на предыдущем этапе, записываются поверх старого изображения, затирая его. Этот способ значительно экономит память, так как данные о яркости содер­жатся в одном массиве. В то же время, метод обычной (нерекуррентной) анизотропной фильтрации, использующий два массива, является более точным, т.к. при этом не накапливаются ошибки, сделанных на предыдущих этапах вычислений. Сглаживающий мас­сив W (m, n) выбирается из тех же соображений, что и при обычной анизотропной фильтрации.

Существенным недостатком линейных фильтров является размывание кромок и других характерных деталей объекта.

Наиболее известными нелинейными методами фильтрации являются медианный фильтр и метод расширения-сжатия.

Медианная фильтрация очень эффективна при по­дав­лении шумов, особенно импульсного характера; при этом сохраняются резкие перепады - кромки. Медианой последовательности x₁, x₂, ...x_n, где n - нечетное, называется средний по значению член ряда, получающегося при упорядочивании последовательности по возрастанию. Для четного n медианой является среднее арифметическое двух средних членов. Например, mediana (0, 2, 5, 0, 8) = 2, mediana (0, 2, 5, 3, 0, 8) = 3.

Медианный фильтр для некоторой окрестности изображения (x, y) описывается выражением:

L_m(x, y) = mediana L(x, y)

где L_m(x, y) - новое значение интенсивности (яр­кости) текущего пикселя изображения, L(x, y) - интенсивность в некоторой окрестности этого пикселя.

Для квадратной апертуры размерностью 33 данная формула будет выглядеть следующим образом:

причем значение пикселя e будет определяться пятым (по возрастанию) значением яркости пик­селей в этой окрестности. Качество фильтрации изображения, как и для линейных фильтров, растет прямо пропорционально размеру апертуры фильтра.

Данный фильтр, как и линейный, может применяться к изображению как рекуррентным, так и нерекуррентным способом. Недостатком медианного фильтра является его очень низкая скорость, поэтому он применяется, как правило, с малыми апертурами (33, 51), а также с изображениями, которые плохо обрабатываются линейными фильтрами.

Вообще, чем больше апертура фильтра, тем лучше удаляются помехи, имеющие большую площадь. Также, для улучшения качества можно использовать несколько проходов, что позволяет уничтожить те помехи, которые остались после первых итераций.

Фильтр типа «сжатие-расширение» применяется только в бинаризованных изображениях, когда испо­льзуются две градации яркости пикселей: объект-фон. Процедура сжа­­тия заключается в уменьшении размеров объекта и уве­личении размеров отверстий (при этом устраняются мелкие фрагменты). В процессе расширения, наоборот, объект увеличивается в размерах, при­чем его полости заполняются, восстанавливая тем самым целостность. Поскольку обе процедуры быстрые, их часто используют вместе, делая многопроходными. Например, сначала выполняется 15 сжатий изображения, а затем 20 расширений.

В зависимости от формы применяемой апертуры различают три типа процедур сжатия-расширения: 8-ми связное, 4-х связное и диагональное. В каждом случае используют апертуры размерностью 33, однако, при 8-ми связном сжатии-расширении используется квадратная апертура (учитываются все пиксели - соседи центрального), при 4-х связном - крестообразная апертура (на­пра­вления сканирования: вверх, вниз, влево и вправо), а при диагональном сжатии-расширении - Х-образная. Во всех процедурах обрабатываются только пиксели, принадлежащие объекту.

Для фильтрации помех и сглаживания изображений при­меняются также различные интегральные методы. К ним относятся дискретные преобразования Фурье, Уолша, Адамара и др. Подобные преобразования, в целом, осуществляются медленнее, чем рассмотренные выше, т.к. требуют большего объема вычислений.

После фильтрации (сглаживания) изображений проводится выделение краев и линий -границ перепада яркости и для дальнейшей обработки используются только элементы, принадлежащие этим границам. При таком пре­д­ставлении изображений, называемом кон­турным, достигается значительное сжатие визуа­ль­ной информации и повышение скорости ее окончатель­ной обработки.

Алгоритмы выделения контуров разделяются на две группы: операторные и корреляционные.

Алгоритмы этой группы основаны на использовании операторов пространственного дифференцирования, которые выделяют в каждом заданном фрагменте изображения элементы, находящиеся на границе различных по освещенности (яр­кос­ти) областей.

Метод определения краев и линий основан на предположении, что соответствующие им точки изображения вызывают экстремумы функции освещенности L и их можно определить по максимумам нормы градиента. Понятие градиента иллюстрирует рис. 6.49.

Градиент освещенности Г_ij в точке (i, j) определяется как двумерный вектор

Фрагменты, в которых работают дифференциальные операторы, задаются на каждом шаге сканирования изображения программным окном. (В про­граммах обработки изображений такое сканирование организуется с использованием операторов цикла).

Простейшие дифференциальные операторы работают в программном окне размерностью 22, и самый простой из них использует только два элемента окна, кроме анализируемого элемента l_ij.

Норма градиента Г_ij определяется выражением:

или, чтобы избежать операций возведения в степень и извлечения корня и ускорить счет:

Г_ij = l_ij - l_i+1,j + l_ij - l_i,j+1

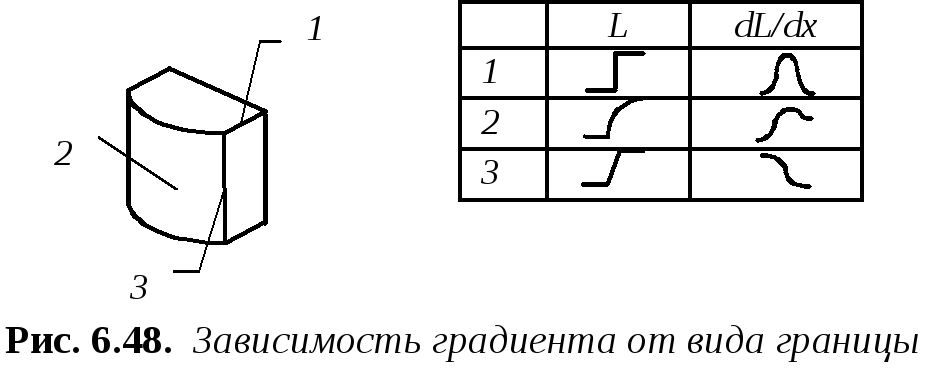
Вид градиента освещенности зависит от формы границы, или, точнее от вида сопрягаемых поверх­ностей, образующих границу (рис. 6.50). Цифрой 1 обозначена граница, образованная двумя плоскостями, цифрой 2 - выпуклая поверхность, цифрой - 3 сопряжение выпуклой поверхности и плоскости.

Самыми популярными дифференциальными операторами являются операторы Робертса и Собеля.

Оператор Робертса (рис. 6.51) позволяет точнее вычислить норму градиента по сравнению с простым дифферен­ци­альным оператором 22, поскольку использует все элементы программного окна. Имеем:

Г_ij = l_ij - l_i+1,j+1 + l_i+1,j - l_i,j+1

Значение Г_ij можно определить с помощью маски, определя­емой выражением:

(В обоих случаях операторы с модулями разности дают большую погрешность определения нормы градиента, чем исходные формулы).

Операторы пространственного дифференцирования, работающие в программном окне размерностью 33, позволяют не только определить норму градиента (т.е. величину перепада яркости), но и проследить линию или контур изображения. Данный оператор обеспечивает одновременно фильтрацию и выделение контура и носит название «око­н­туриваю­щего фильтра».

Оператором Собеля (рис. 6.52) норма градиента Г_ij находится следующим образом:

Г_ij = Гx_ij + Гy_ij,

причем предварительно вычисляются нормы градиента по координатам X и Y кадра:

Гx_ij = (l_i+1,j-1 +2l_i+1,j +l_i+1,j+1) - (l_i-1,j-1 + 2l_i-1,j + l_i-1,j+1),

Гy_ij = (l_i-1,j+1 +2l_i,j+1 +l_i+1,j+1) - (l_i-1,j-1 +2l_i,j-1 + l_i+1,j-1).

Направление контуров и линий оценивается по соотношению значений Гx_ij и Гy_ij.

Используя маски для определения Гx_ij и Гy_ij получим для нормы градиента Г_ij следующее выражение:

После применения данного оператора, на выходе алгоритма образуется массив, каждый элемент которого соответствует величине градиента в данной точке изображения. (На рис. 6.50 и 6.51 для наглядности изображения объекта инвертированы).

Недостатком обоих операторов является их неприемлемость для «толстых» контуров. С этой целью, иногда используются методы «утончения» контура. Известен алгоритм утончения, основанный на раздельном сканировании внешнего и внутреннего контуров и последующем определении тонкого контура, как среднего значения между точками обоих контуров. Такой подход требует применения алгоритмов обхода контура (связанных с процедурами сегментации и кодирования).

Вторая производная изображения определяется с помощью преобразования Лапласа. Оператор Лап­ласа _ij является оператором производных второго порядка. Он представляется в виде процедуры:

; или в виде маски