5.3.1. Звук и его основные характеристики

Распространение звука (в том числе и УЗ) описываетсяволновым уравнением, единым для всех частот:

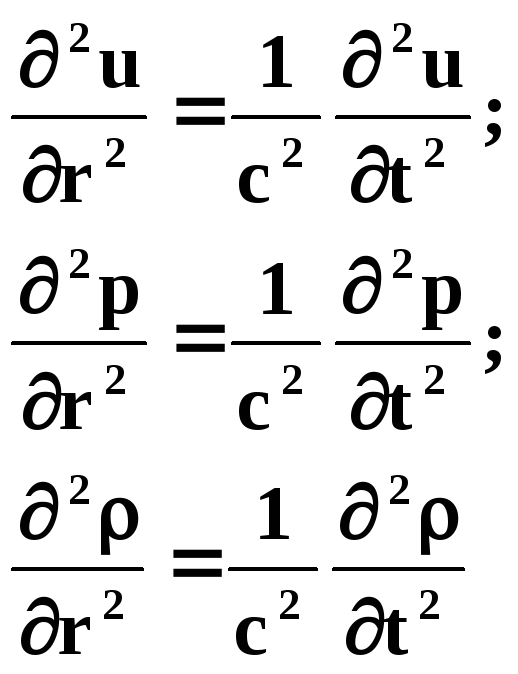
где u,  и p - смещение частиц среды (амплитуда волны), ее плотность и давление, r и c - соответственно дальность распространения и скорость волн.

Частотное уравнение для звука имеет тот же вид, что и для других волн. Оно определяет длину волны гармонического колебания (тона) , распространяющегося со скоростью c:

 = c/f = cT.

Чистые звуки - тона встречаются крайне редко. Обычно звук представляет собой сложное колебание, которое представляют в виде спектра (суммы гармоник) с кратными часто­тами (обертонами) 2f, 3f, и т.д. ... У гармонического колебания спектр состоит из одной частоты. Периодические колебания, состоящие из набора основной частоты и кратных ей, имеют линейчатый спектр (рис. 5.32). Для непериодических колебаний (шумов) характерны сплошные спектры.

Применительно к звукам речи, различают слово - наименьшую смысловую единицу и фонему - наименьшую звуковую единицу данного языка. Например, в русском языке имеется 41 фонема, образующая 6 гласных звуков (а, о, у, э, и, ы) и 35 согласных. Количество фонем превосходит количество букв, т.к. большинству согласных звуков соответствуют две фонемы - мягкая и твердая. Произносимые звуки могут значите­льно отличаться от фонем (также как рукописная буква отличается от типографического курсива: к примеру, в тексте «лоб второго», в речи «лоп фтарова»). Области максимальных уровней спектра называются формантами. Именно представление звуков в виде фонем и формант (т.е. использование лингвистических принципов) позволяет строить системы распознавания речи.

Нижняя граница области УЗ частот, от­де­ля­ющая ее от области слышимого звука, определяется субъективными свойствами че­лове­чес­кого слуха и является условной.

Верхняя граница УЗ обусловлена физической природой упругих волн, которые могут распространяться лишь при условии, что  >> D_экв, где D_экв - длина свободного пробега молекул в газах или межатомные расстояния в жидкостях и твердых телах. Следовательно, верхняя граничная частота УЗ f_в определяется из условия:

f_в = 1/D_экв

Для газов при нормальном давлении f_в  10⁹ Гц, а для жидкостей и твердых тел достигает 10¹² ... 10¹³ Гц.

В зависимости от длины волны УЗ обладает специфическими особенностями передачи и распространения, поэтому область УЗ частот удобно разделить на три диапазона:

• низкие частоты (1,5 10⁴ ... 10⁵ Гц);

• средние (10⁵ ... 10⁷ Гц);

• высокие (10⁷ ... 10⁹ Гц).

• гиперзвук (10⁹ ... 10¹³ Гц).

Для АЛС по сравнению с ЭЛС характерна значительно меньшая (на несколько порядков) скорость распространения сигналов. Она лежит в пределах 2 10² … 1,5 10³ м/c - для газов, 5 10² … 2 10³ м/c - для жидкостей и 2 10³ … 8 10³ м/c - для твердых сред. Такие малые скорости, и, следовательно, малые длины волн намного повышают разрешающую способность УЗ методов по отношению к электромагнитными при равных частотах.

Длина волны УЗ зависит от частоты и среды распространения. Так, для воздуха в самой низкочастотной области  не превышает нескольких сантиметров. В случае высоких УЗ частот значения  составляют 3,4 10^-5 ... 3,4 10^-7 м в воздухе, 1,5 10^-4 ... 1,5 10^-6 м - в воде, 5 10^-4 ... 5 10^-6 м - в стали.

Особенностью УЗ высокочастотного и гиперзвукового диапазонов является возможность применения к нему методов квантовой механики, поскольку длины волн и частоты в этих диапазонах становятся одного порядка с параметрами, характеризующими структуру вещества. Упругой волне данной частоты сопоставляется квазичастица - фонон или квант звуковой энергии. Квантово-механические представления применяют при рассмотрении взаимодействий в твердых телах.

Для оценки амплитуды звуковой волны используются косвенные величины: акустическое давление p = cv, упругое смещение частиц среды u и их колебательная скорость v = du/dt. В свою очередь, характеристикой акустического давления в среде является интенсивность или сила звука, определяемая через энергию звуковой волны.

Интенсивностью звука J называется величина, равная средней по времени энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения в единицу времени (т.е. удельной мощности W_уд). Для плоской синусоидальной бегущей волны:

или J = p v/2

Параметр Z =  c получил название характеристического импеданса среды. (Наряду с Z также используется акустический импеданс Z_а = p/v, зависящий не только от свойств среды, но и от условий отражения, углов падения и других факторов).

В стоячей волне J = 0, т.к. она не переносит энергию. Интенсивность звука измеряется в Вт/м² и лежит в пределах 10^-12 (нижнее пороговое значение) … 10⁶ (значение в фокусе УЗ концентратора). В частности, в задачах акустического контроля применяют АЛС звукового и УЗ диапазонов с частотами 50 Гц ... 50 МГц и интенсивностью  10³ Вт/м².

Интенсивность звука обратно пропорциональна квадрату расстояния r от источника, зависит от Z и возрастает пропорционально квадрату амплитуды p и частоты f сигнала: J  (1/r², Z, р², f²). Следовательно, на высоких УЗ частотах могут быть получены сигналы огромной силы. Так, в мегагерцовом диапазоне в излучателях АЛС легко достигается J  10^-3 Вт/м², что в 1000 раз сильнее звука пушечного выстрела. Зависимость силы звука от Z приводит к тому, что в более плотных средах меньшие звуковые давления вызывают большую интенсивность звука. В частности, для получения больших интенсивностей используется принцип «излучения в воду». В этом случае, та же сила звука будет достигнута при 60-ти кратном запасе по амплитуде звукового давления, величина которой лимитируется прочностью излучателя.

Громкость £слы­шимых звуков при одинаковой интенсивности зависит от его частоты. За единицу громкости принят сон - громкость тона (чистого звука) частотой 1 кГц при интенсивности 40 дБ. (Для примера, шепот человека оценивается в 20 дБ, крик - в 40, болевой порог - в 130 дБ). Часто для определения громкости применяют относительные логарифмические единицы - децибелы, показывающие, насколько звуковое давление p сигнала превосходит порог чувствительности уха. Установлено, что минимальное давление p₀, которое способно воспринять че­ловеческое ухо, составляет  2 10^-5 Н/м². Для сравнения: величина давления, при котором разрушается барабанная перепонка равна 2 10³ Н/м². Следовательно, £ = 20lg (p/p₀). Вообще говоря, логарифмическая единица измерения отношений мощностей W или энергий называется бел. £^* = lg W₁/W₂. (Обычно употребляется 1/10 доля бела, или децибел).

Громкости некоторых источников звука приведены в табл. 5.3.

Таблица 5.3. Громкости различных источников звука

Источник звука	Громкость £, дБ
Тихая комната	30
Шум оживленной улицы	60
Шум самолета на расстоянии 1 м	115
Болевой порог	130

К основным законам распространения звука относятся:

• законы отражения и преломления звука на границах сред (рис. 5.33);

• законы дифракции и рассеяния звука при наличии препятствий и неоднородностей на границах;

• законы волноводного распространения в ограниченных участках среды.

В большинстве случаев построения АЛС для задач локации и связи ограничиваются моделью геометрической или линейной акустики, в которой рассматриваются только первый и третий законы распространения. Эта модель соответствует зоне упругих деформации среды распространения УЗ. Характер распространения УЗ волн зависит от соотношения между  звука и характерным (для условий его распространения) геометрическим па­ра­мет­­ром d_хар (размером источника звука или пре­пятствия на пути волны, размером неоднородностей среды, поперечного сечения волновода и т. п.). В рамках линейной модели принимается d_хар >> .

Второй закон учитывается в задачах акустической диагностики и звуковидения. Степень отклонения от геометрической картины распространения и необходимость учета дифракционных явлений определяется параметром гдеr - расстояние от точки наблюдения до объекта, вызывающего дифракцию.

Третий закон распространения имеет очень большую роль в задачах гидроакустической связи, описывая явление «под­водного звукового канала». Этот канал, образуется на некоторых глубинах моря вследствие стратификации - неравномерного распределения температуры и плотности воды с глубиной. Указанная неравномерность приводит к тому, что характеристический импеданс среды на некоторой глубине локально уменьшается. Образующийся волновод достигает сотен километров длины и может использоваться для передачи сигналов с малым затуханием.

Отражение звука от объектов приводит к появлению эха и реверберации.

Область применения линейной акустической модели УЗ определяется двумя основными факторами - интенсивностью звуковых волн и их частотой. Так, при увеличении интенсивности J волн в их поле проявляются многочисленные нелинейные эффекты (нарушается принцип суперпозиции, изменяется форма волны, а ее спектр обогащается высшими гармониками и т.д.). Критерием применимости аппарата линейной акустики служит выражение вида:

М = v/c << 1,

где М - число Маха. Данное неравенство означает, что колебательная скорость частиц среды v должна быть много меньше скорости распространения звука в этой среде. Это выражение выполняется довольно часто. Так, для звука в воздухе, интенсивность которого соответствует громкому разговору М  10^-6. Даже вблизи мотора реактивного самолета v  250 см/с, и, следовательно, при скорости звука в воздухе с = 342 м/с, М < 0,01.

Роль нелинейных эффектов в звуковом поле возрастает и с частотой. Действительно, для гармонической волны частотой f колебательная скорость определяется формулой: v = 2 f u и тогда M = 2 f u/c.