7.5. Организация управления роботом с силомоментным очувствлением

К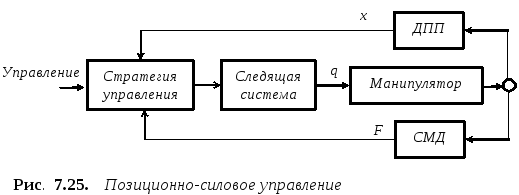ак уже отмечалось, характеристики ССО роботов должны выбираться исходя из параметров конкретного робота и особенностей технологической операции. Так, например, для большинства контактных задач свойственно временное за­мыкание и размыкание кинематической цепи. В этом случае, использование только позиционного или только силового управления недостаточно. Традиционным подходом является построение нескольких контуров регулирования. Если система управления является позиционной, то сигналами от СМД производится модификация номинальной траектории или скорости командами от СМД [ ]. Общая схема позиционно-силовой системы управления робота приведен на рис. 7.25.

Теперь рассмотрим влияние жесткости СМД С на динамику антропомо­рфного ма­нипулято­­ра с позиционно-си­ло­вой си­стемой уп­ра­вле­ния. Управление приводами в режиме замкнутой кинематической цепи производится по сигналам СМД, причем на каждом шаге движения выполняется решение прямой кинема­тической задачи - определение по обо­бщенным координатам q положения концевой точки манипулятора R. Если ССО построена в соответствии с концепцией «очу­­вствленно­го запястья», то возникает необхо­димость проведения вы­чис­лений в трех ко­орди­натных си­с­­темах: системе ко­ординат СМД (здесь находится «центр измерений»), абсолютной системе координат робота OXYZ и системе обобщенных координат q. Запишем: R = J (q₀) q. [ ], где матрица Якоби J(q₀) размера (n6) определена для конфигурации манипулятора q₀ и n - количес­тво его степеней подвижности. Приведем вектор усилий F из центра измерений датчика в систему обоб­щенных координат. Сделаем допущение, что точка приложения вектора F приблизительно совпадает с центром измерений. Тогда, в соответствии с [ ] получим:

F_q(q₀) = J^Т (q₀) F,

где F_q - вектор внешних сил, приведенный к обобщенным координатам исполнительного механизма. Принимая для простоты расчета, что жесткость собственно манипулятора С_м намного больше жесткости датчика C, т.е. уподобляя датчик некоторому упругому шестикомпонентному упору, получим:

F_q(q₀) = C_q(q₀) q,

Здесь параметр C_q(q₀) можно назвать матрицей обобщенной жесткости СМД.

Поскольку для «упругого упора» справедливо равенство F = C R, то обобщенная жесткость СМД в точке q₀ определится зависимостью:

C_q(q₀) = J^T (q₀) C J(q₀).

Следовательно, уравнение динамики манипулятора с запястным СМД в окрестности точки контакта запишется следующим образом:

A(q₀) q + (dF_к/dq) q = Q(q₀) + J^T (q₀)CJ(q₀) q,

где A(q₀) - матрица инерции механической системы робота, F_к(q, dq/dt) - вектор центробежных и кориолисовых сил, Q(q₀) - вектор активных обобщенных сил манипулятора (например, вектор моментов, развиваемых приводами).

Таким образом, сигнал управления исполнительным механизмом Q*(t) должен формиро­ваться в виде:

Q*(t) = Q [R, A, C, J(q₀), t]

Данное выражение показывает, что для обеспечения заданного качества управления необходимо учитывать, наряду с другими факторами, жесткость СМД и конфигурацию исполнительного механизма робота. Другими словами, система, устойчивая при одной кон­фигурации манипулятора может потерять устойчивость при ее изменении. В частности, это характерно при работе манипулятора в большой зоне обслуживания, например, для технологических операций, подобных абразивной зачистке.