1.3. Способы компенсации и учета погрешностей

Во всех случаях погрешность датчика стремятся уменьшить. В некоторых случаях ее удается полностью или частично скомпенсировать. В других, когда компенсация невозможна, погрешности учитываются и вводятся в паспорт датчика.

Источники систематических погрешно­стей могут быть очевидными, непосредст­венно вызываемыми условиями работы (например, вибрациями), а могут быть «скрытыми» от прямой регистрации. Для этого случая, необходимо, чтобы влияющая функция изменялась со временем, тогда систематическую погреш­ность можно об­наружить и компенсировать. В противном случае, ее очень сло­­ж­но за­метить. Единст­вен­ным способом обнару­жения является пери­оди­ческая поверка нуля и чувствитель­ности по образцовым мерам.

Для компенсации систематической погрешности на практике используются три основных способа - аналитический, методический и схемотехнический.

Аналитический способ основан на введении в исходную формулу известных аналитиче­ских выражений. Например, для датчиков на основе металлических ЧЭ, функция преобразования зави­сит от температуры:

y = f(x, T^о),

В общем случае y = S x или в производных:

При x ¹ f (T^o) имеем

Пусть известна относительная мульти­пли­ка­тив­ная температурная чувствитель­ность S_k^T = S/T, то

 y+dy = [S+S_k^T dT] x

Тогда, зная реальную температуру датчика определяют DT = T-T_ном , и за­ме­няя dT на DT получают окончательно

 y^T= S_ном x + S_k^T DT x

Второе слагаемое в правой части этого выражения представляет собой поправку в результат измерения.

Характерным примером применения методического способа является компенсация погрешности, вызванной магнитным полем Земли. Измерения проводят дважды: первый раз - при любом положении датчика, а при повторном его ори­ентацию меняют на 180^о.

Схемотехнический способ предполагает такое построение датчика, при котором отдельные составляющие погрешности взаимно компенсируются. Для этого могут использова­ться, например, сим­метричные мостовые схемы, частично ком­пенсирующие температурную погрешность.

Функция преобразования симметричного моста Уитстона (рис. 1.17) определяется выражением:

U  = E S_r (r₁ + r₄ - r₂ - r₃),

где E - напряжение питания, S_r - чувствительность пле­­­ча. Стрелками показаны условные направления деформаций под действием влияющих факторов.

Изменение температуры вызывает вариации номиналов плеч моста Dr. Тогда получим

U_D  = E S_r [(r₁+Dr₁) + (r₄+Dr₄) – (r₂+Dr₂) – (r₃+Dr₃)].

Если значения Dr для всех плеч одинаковы, то U_D= U.  

Случайные погрешности приводят к разбросу результатов при повторных измерениях. В большинстве случаев их компенсация представляет собой сложную задачу, однако, иногда их можно устранить защитой измерительного канала от вызывающей причины. С этой целью используют температурную и вибрационную стабилизацию, электромагнитное экранирование и пр. Существует ряд схемотехнических решений - симметричные дифференциальные схемы, применение корреляционных методов и т.д. Примером дифференциальной схемы является измерительный мост, позволяющий компенсировать синфазные случайные погрешности (если источник этих погрешностей действует одновременно на все 4 плеча моста).

Если же случайные погрешности устранить не удается, используют статистическую обработку результатов измерения с целью определения наиболее вероятного значения измеренной величины и пределов погрешности. Результаты измерения и их расхождение характеризуются следующими показателями:

• мате­­ма­­­ти­­­че­ским ожиданием (средним значением по множеству) , где N - количество измерений;

• средней квадратичной погрешностью s_у 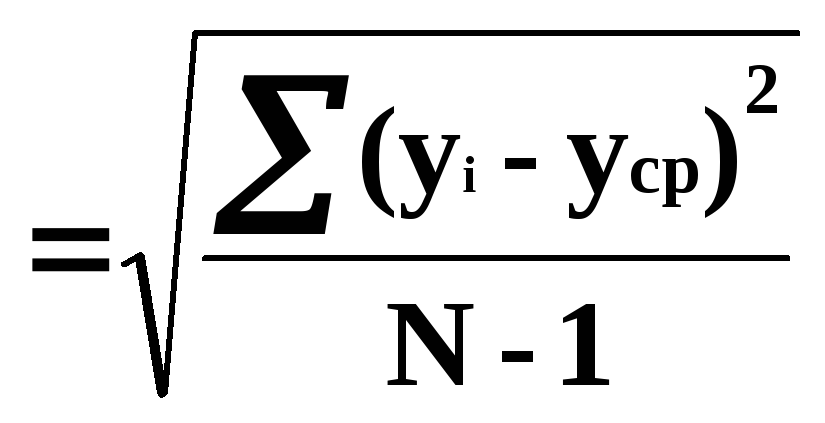и дисперсией . Если погрешности, сопровождающие различные измерения взаимно независимы, то вероятность их появления описывается нормальным (Гауссовым) распределением Р(у).

В этом случае, наиболее вероятное значение равно у_ср, а вероятность появления результатов измерения в указанных пределах равна:

Р(у_ср ±s) = 68,27%, Р(у_ср ±2s) = 95,45%, Р(у_ср ±3s) = 99,73%.

Случайные погрешности также бывают абсолютными, относительными и приведенными. В частности, относительная среднеквадратичная погрешность e_у = s_у/у_ном (в расчетах у_ном приравнивают математическому ожиданию, т.е. принимают у_ном = у_ср).

Использование дисперсионных оценок позволяет суммировать статистически независимые погрешности для любых законов распределения.

Для определения случайных погрешностей иногда применяют квантильные оценки (рис. 1.18). Квантильная оценка - это указание максималь­ного значения случайной погрешности (e_у)_max с заданной доверительной вероятностью P(у).

Общепринятые оценки доверительных вероятностей:

• P(у) = 0,80 - в стандартах надежности средств электроники, автоматики и из­мерительной техники;

• P(У) = 0,9 ... 0,95 - предпочтительные значе­ния при нормировании случайных по­грешностей средств измерения.

Основной недостаток оценки погрешности доверительными вероятностями - это невозможность суммирования значений погрешностей несколь­ких датчиков.

В соответствии с ГОСТ 8.011-72 при проведении метрологической поверки датчика необходимо указывать закон распределения погрешностей. В ряде случаев близкие по форме законы приводятся к одному виду.

Законы распределения классифицируются по трем основным при­знакам:

1. По форме: симметричные (нормальный, треуголь­ный и пр.) и скошенные.

2. По числу максимумов в кривой распределения: безмодальные, од­­номодальные и двухмодальные.

3. По способу аналитического описания: экстремальные (в частности, дискретное двузначное рас­­пределение), симметричные экспоненциаль­ные, композиционные и частные (напри­мер, арксинусоидальный).

Приедем некоторые примеры законов распределения типовых погрешностей (рис. 1.19).

• погрешность от зазора в кинематической цепи рас­пределена по дискрет­ному двузначному за­кону, т.к. прини­мает только два значения:  +a,  -a (рис. 1.19 а);

• погрешность от гистерезиса имеет композиционное распределение - в виде суммы дискрет­ного двузначного и экс­по­ненци­ального за­конов и имеет размытость около точек  +a,  -a (рис. 1.19 б);

• погрешность от квантования распреде­лена по рав­номерному закону, т.к. зна­чений больших +b, и меньших -b не встречается, а внутри этого интервала они равновероятны (рис. 1.19 г);

• погрешность от синусоидальной наводки рас­пре­делена по арксинусоидальному закону;

• погрешность градуировки имеет вид композиции равномерного и экспоненциального распределений;

• темпе­ратурная погрешность имеет вид компози­ции треугольного асимметрич­ного и дискретного двузначного рас­пределе­ний; погрешность от колебаний на­пря­же­ния питания распределена по треугольному закону.

Закон распределения погрешностей для электронных систем общепромышленного назначения обычно известен. Например, шумы радиоаппаратуры подчинены нормальному закону распределения (рис 1.19 в).

Применение рассмотренных выше характеристик для оценки точности датчика, предполагает составление соответствующего паспорта. Иногда же для этих целей удобно использовать следующие интегральные оценки: постоянство, правильность, точность.

Постоянство датчика - это такое его свойство, для которого характерны малые случайные погрешности (рис. 1.20). В этом случае, обе­спечивается высокая сходимость результатов измерений.

Правильностью (рис. 1.21) называется способ­ность датчика выдавать резуль­тат с малой систематической погрешно­стью. (Наиболее ве­роят­ное зна­чение изме­ряемой величины близко к истинному).

Точность обозначает свойство датчика давать результаты, индивидуально близкие к ис­тинному значению измеряемой величины. Од­но­­временно обес­печиваются высокие постоян­ство и правильность (рис. 1.22). Численно точность выражается через суммарную погрешность, учи­тыва­ю­щую как случайную, так и систематическую состав­ляющую, которая определяет доверительный интервал вокруг измеренного значения, вну­три которого с задан­ной вероятностью находится истинное значение измеряемой величины.

Подводя итоги данной главы отметим основные требования, которые следует соблюдать при разработке датчиков робототехнических и мехатронных систем.

1. Необходимо выделить измеряемый параметр и выбрать методику измерения.

2. Разработать структуру информационных модулей, максимально используя симметричные и дифференциальные схемы.

3. Определить влияющие факторы и сформировать рабочие условия функционирования датчика.

4. Провести градуировку датчика и определить его функцию преобразования.

5. Вычислить значение относительной систематической погрешности.

6. Провести серию испытаний и определить закон распределения случайных погрешностей, а затем вычислить математическое ожидание и дисперсию случайных погрешностей датчика и определить значение относительной случайной погрешности.

7. Провести расчет суммарной погрешности и указать значение доверительного интервала.

8. Составить итоговый паспорт на датчик.