Общие сведения о датчиках информационно-измерительных систем

Глава 1. Общие сведения о датчиках информационно-измерительных систем

Практика измерений в России имеет тысячелетнюю историю. Еще во времена Киевской Руси, в ходу были «антропо­метрические» единицы - вершок, пядь, локоть. Первая попытка стандартизации измерений датируется 1070 г., когда великий князь Святослав Ярославович ввел в качестве меры длины свой «золотой пояс». Весовые меры (осьмины) появи­лись во времена Ивана Грозного и были узаконены Двин­ской гра­мо­той. Петр I допустил к хожде­нию в России английские меры (футы, дюй­мы). В XIX веке Россия делала попытки ввести единые стандарты на все основные физические величины. По инициативе Петербургской академии Наук в 1875 г. была собрана Парижская конференция, на которой было учреждено Международное бюро мер и ве­сов. Эта организация оказалась не слишком эффективной. Только через 85 лет, в начале 60-х годов ХХ века под руководством профессора Г.Д. Бурбона создается международная комиссия по разработке единой системы проведения измерений. С 1963 года существует меж­дуна­род­ное соглашение по предпочтитель­ной системе метрологических единиц (SI).

1.1. Датчики и их характеристики

Датчик (измерительный преобразователь) - это устройство, обеспечивающее функциональное преобразование изменения одной величины в изменение другой величины, участвующей в некотором информационном процессе.

Рассматривая физические процессы во всех преобразователях, можно в каждом случае устано­вить связь между выходнойy и входной х величинами (рис.1.1), изменяющимися во времени:

y = f (x);

здесь  x - измеряемая величина, а y - результат измерений.

Математическое (или графическое) описание этой связи называется функцией пре­образования датчика (рис. 1.2).

В большинстве случаев при рассмотре­нии структуры датчиков абстрагируются от достаточно сложного представления о преобразо­ва­нии информации в пользу процесса преобразования величин, сигналов и т.д. В этом случае, информационные характери­стики датчиков, в том числе его функция преобразования, определяются на основании анализа преобразования сигна­лов в системе.

Для датчиков с линейной функцией преобразования используется понятие коэффициента преобразования K:

,

где x_i , y_i - текущие значения   x, y.

В зависимости от количества измеряемых параметров датчик может описываться одномерной или векторной функцией преобразования (примерами являются однокомпонентный датчик силы и силомоментный датчик). Датчик, имеющий векторную функцию преобразования Y = F(X) является многокомпонентным.

Вообще говоря, любой датчик можно считать многокомпонентным, поскольку на него кроме измеряемой величины действуют влияющие факторы, обусловленные внешними причинами. Тем не менее, мы под многокомпонентным датчиком будем понимать такой преобразователь, который конструктивно предназначен для измерения нескольких параметров. Особенностью многокомпонентного датчика является взаимное влияние каналов измерений (рис. 1.3) Для оценки этого свойства измерителя используется понятие избирательности каналов.

Избирательностью k-ого канала изме­ритель­ной системы называется выражение вида:

; k ¹ j,

где y_k - номинальное значение измеряемой вели­чины (компоненты).

Для линейных систем избирательность характе­ри­­зуется коэффициентом влияния каналов lⁱ½_j:

;

здесь  y_i, y_j - сигналы на выходах  i-ого и j-ого  каналов; x_j - входное воздействие на  j-ый канал.

В частном случае,  при отсутствии влияния каналов - y_j = 0, т.е. на выходе канала образуется сигнал пропорциональный только измеряемой величине.

Если функции изменения сигналов дифференцируемы, то под чувствительностью датчика будем понимать величину S, равную:

Чувствительность - важнейшая характеристика дат­чика, позволяющая оценить выходной сигнал по пределам изменения измеряемой величины и выбрать датчик, отвечающей требованиям измерения. Для линейных преобразователей  S = K, и  y = Kx = Sx, причем размерности  K и S одинаковы, например [В/н].

Чувствительность, в общем случае, зависит от внешних факторов: напряжения питания, температуры, а также спектра и частоты измеряемого воздействия. Например, в паспорте на диф­фе­ренциаль­ный трансформатор T1ON фирмы Ifelec, Франция указывается его чувствительность S₁ = 1,5 мВ/мм/В при частоте напряжения питания 50 Гц и S₂ = 17 мВ/мм/В при 400 Гц.

Чувствительность датчиков определяется в статическом и динамическом режимах работы.

Статическая чувствительность дат­чика S_c измеряется на основании его статической функции преобразования, причем  S_c = K и совпадает с  S в том случае, если статическая характеристика является пря­мой, проходящей через начало координат.

Динамическая чувствительность S_д, строго опреде­ляется лишь для случая, когда измеряемая фу­н­кция x является периодической функцией времени. В этом случае, выходной сигнал y имеет ту же периодичность, что и  x. Например, если x(t) = x₀ + x₁ cos wt, то y(t) = y₀ + y₁ cos (wt +y), где w - круговая частота, w = 2pf, f - частота входного сигнала (в Гц).

Обычно изменения измеряемой величины не являются гармоническими функциями, они могут сложным образом зависеть от времени. Если функцию x(t) разложить в ряд Фурье, то выходной сигнал y(t) будет представлять собой суперпозицию различных соста­в­ля­ю­щих y_n(t):

Здесь координаты x₀, y₀  - определяют рабо­чую точ­ку Q₀ на статической градуиро­вочной харак­теристике, y - сдвиг фазы между вариациями сигналов на входе и выходе.

Зависимость чувствительности  S_д от частоты в динамическом режиме определяет час­тот­ную характеристику дат­чика. Изменения  S_д в функции частоты зависят от механической, тепловой и электрической инер­ции преобразователя, т.е. его массы m, электрического сопротивления R, индуктивности L и емкости C.

Частотные характеристики датчика связаны с порядком дифференциального урав­нения, опи­­­сывающего его конструктивную схему. В соответствии с этим выделяют датчики первого и второго порядка.

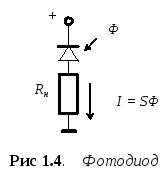
Датчики первого порядка в своей структуре не содер­­жат колеблющихся частей. К ним относятся, например, оп­тические преобразователи - свето- и фотодиоды. На рис. 1.4 представлена схема фотодиода. Обозначено: Ф - све­товой поток, I - ток, R_н - сопротивление нагрузки.

Функция преобразования датчика первого порядка описывается дифференциальным уравнением первого порядка:

,

где  A и B - константы.

В комплексной форме соответствующие переменные будут равны:

где  x₁, y₁ - действительные величины.

Уравнение датчика первого порядка в комплексной форме примет следующий вид:

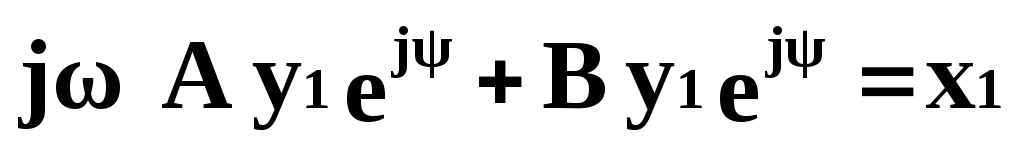
Подставляя значение граничной частоты  f_г= B/2pA, получим

y = -arctg (f/f_г).

Таким образом, частотная характеристика датчика 1-го порядка определится зависимостью:

,  или

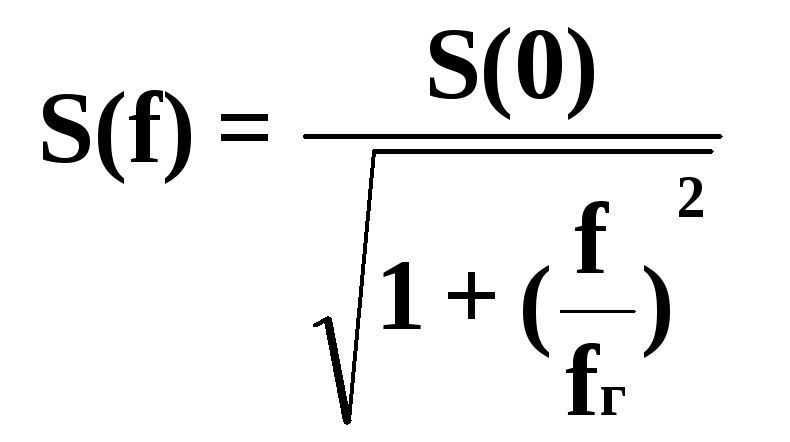
Например, для фотодиода (рис. 1.4) получим:

В частном случае, при  f << f_г,  S(f) = S(0) . Вид амплитудно- и фазочастотных характеристик (АЧХ и ФЧХ) представлен на рис. 1.5.

Датчики второго порядка (напри­мер, акселерометры) содержат в своей структуре колеблющиеся элементы и характеризуются значениями собственной частоты  f₀ и затуханием z. Они описываются дифферен­циаль­ным уравнением вида:

где  f₀ = (1/2p) ÖC/A,  z= B/(2ÖCA).

Частотная характеристика датчика 2-го порядка определяется за­висимостью:

Принято считать, что оптимальное значение коэффициента затухания z лежит в пределах 0,6 … 0,7. Частотные характеристики датчика второго прядка представлены на рис. 1.6.

Полоса пропускания датчика  B - это диапазон частот, в котором ординаты амплитудной частотной характеристики уменьшаются относительно их максимального значения не более чем на 3 дБ (рис. 1.7). В расчетах можно считать, что полоса пропускания соответствует горизонтальному участку АЧХ.

Для датчиков 1-го порядка имеем, 20 lg S(f_г)/S(0) = 3 дБ, т.е. B = f_г. Ширина полосы пропускания датчиков 2-го порядка зависит от z. При z = 0,6 … 0,7, B » f₀.

Датчик называется линейным в некотором диапазоне измеряемых величин, если его чувствительность не зависит от значения измеряемой величины. В диапазоне линейности выходной сигнал пропорционален измеряемому параметру.

• в статическом режиме:  S = K = S(0),

• в динамическом:

- для датчика 1-го порядка и - для датчика 2-го порядка.

Итак, линейность в динамическом режиме зависит от чувствительности статического режима S(0) и параметров частотной характеристики (f_г, f₀, z). В частном случае, когда датчик работает только в динамическом режиме (это характерно, например, для акустического дальномера) S(0) = 0.

На практике линейность датчика определяется по его градуировочной харак­теристике. При ее построении распределе­ние экспериментальных данных аппрокси­мируют уравнением некоторой прямой, используя метод наименьших квадратов. Напомним, что в этом случае сумма квадратов отклонений e_у эксперимен­таль­ных точек от полученной прямой минимальна.

Установлено, что приближение к прямой вида  y = a x + b,

достигается при и, где N - число точек аппроксимации.

Поведение датчика в установившемся режиме описывается его АЧХ. Поведение же в переходных режимах зависит от его инерционных свойств. Характер переходного режима не зависит от закона изменения измеряемой величины, а только от свойств элементов собственно датчика. Быстродействия - это параметр датчика, поз­воля­ющий оценить, как выходной сигнал следует во времени за изменением измеряемой величины. Быстродействие, таким образом, характеризует время, необходимое для того, чтобы вклад переходного режима в выходную величину стал пренебрежимо мал в условиях заданной точности. Параметр, ис­поль­зуемый для количественного описания быстродействия, называется временем установления. Время установления t_уст - это интервал времени, который дол­жен пройти после ступенчатого изменения измеряемой величины, чтобы сигнал на выходе достиг уровня, отличающегося от входного не более чем на e %.

Различают четыре составляющих времени установления t_уст (рис. 1.8): вре­мя задержки  на­растания t_зн, - время, соответствующее увеличению сигнала на выходе датчика на 10% от начального; время нарастания t_н - время, необходимое для изменения выходного сигнала от 10% до 90%; вре­мя задержки спада t_зс - время, соответствующее уменьшению сигнала на выходе датчика на 10% от установившегося значения (до 90%) и вре­мя  спада t_с - время, требуемое для уменьшения выходного сигнала от 90% до 10% установившегося значения.

Поскольку динамика датчиков 1-го порядка в переход­ном режиме описывается уравнением вида:

A dy/dt +By = x₀

То решением этого уравнения при начальных условиях y = 0, t = 0 будет

где у₀ = х₀/B и t =A/B = 1/2pf_г - установившееся значение и постоянная времени датчика соответственно.

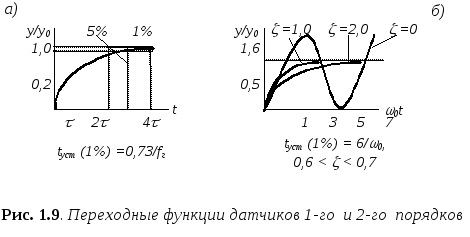
Время установления t_уст можно определить по графику переходного процесса (рис. 1.9а). Так, время установления t_уст (1%) = 4,6 t = 0,73/f_г. Для t_уст (10%) справедливо: t_уст (10%) = t_н = t_с = 2,2t. Следовательно, чем выше граничная частота, тем выше быстродействие датчика.

Уравнение датчика 2-го порядка в переходном режиме имеет вид:

A d²y/dt² +Bdy/dt + Cy = x₀

При тех же начальных условиях решение будет зависеть от коэффициента затухания z = B/2ÖCA. Время установления будет минимальным при z = 0,6 ... 0,7 (рис. 1.9б). В этом случае t_уст (1%) = 6/w₀. t_уст (10%) = t_н = t_с = 2,4/w₀, причем w₀ = 2pf₀ = ÖC/A.

Часто, при оценке переходных процессов наряду с коэффициентом затухания z используется понятие декремента затухания d. Декремент затухания - это величина, обратная числу колебаний, по истечению которых максимальное значение амплитуды убывает в е раз.

d =ln y₀/y₁.

где е - основание натуральных логарифмов, е » 2,718.

От быстродействия следует отличать произво­ди­тель­ность устройства (обычно характерную для цифро­вых систем). Она определяется количеством операций в секунду.

На быстродействие влияют в том числе, факторы не связанные непосредственно с датчиком, например, среда. Так, для резистивного термометрического зонда t_уст (10%) составляет 2,6 с в воде, текущей со скоростью 0,2 м/c и 40 с в воздухе, движущемся со скоростью 1 м/c.

Требования чувствительности и быстродействия противоречивы, что необходимо учитывать при расчетах.