
- •Физические основы классической механики
- •I. Механика. Общие понятия
- •2. Кинематика точки
- •3. Скорость
- •4. Ускорение
- •5. Примеры
- •I. Основные понятия
- •2. Законы механики
- •3. Инерциальные системы отсчёта (и.С.О.)
- •4. Принципы относительности Галилея
- •5. Закон сохранения импульса
- •6. Реактивное движение
- •7. Центр инерции
- •I. Работа
- •2. Энергия
- •3. Кинетическая и потенциальная энергии
- •4. Закон сохранения механической энергии
- •5. Удар абсолютно упругих и неупругих тел
- •I. Кинематика вращательного движения
- •2. Кинетическая энергия вращательного движения. Момент инерции.
- •3. Основное уравнение динамики вращательного движения
- •4. Момент импульса. Закон сохранения момента импульса
- •I. Принцип относительности
- •2. Постулаты Эйнштейна
- •3. Преобразования Лоренца
- •4. Замедление времени
- •5. Сокращение длин
- •6. Сложение скоростей в теории относительности.
- •7. Изменение массы со скоростью
- •8. Движение релятивистской частицы
- •9. Связь между массой и энергией
- •10. Кинетическая энергия. Энергия и импульс
- •Колебания и волны
- •1. Общие сведения о колебаниях
- •2. Механические колебания
- •3. Энергия гармонических колебаний
- •1. Предмет молекулярной физики
- •2. Термодинамические параметры.
- •3. Идеальный газ
- •4. Основное уравнение мкт газов для давления.
- •5. Газовые законы как следствие молекулярно-кинетической теории.
- •1. Скорости теплового движения молекул
- •2. Распределение молекул по скоростям (Закон Максвелла)
- •3. Закон распределения Больцмана
- •4. Число столкновений и средняя длина свободного пробега молекул
- •1. Внутренняя энергия идеального газа
- •2. Первое начало термодинамики
- •3. Работа при расширении газа
- •4. Теплоемкость идеальных газов
- •5. Адиабатический процесс
- •1. Характеристика тепловых процессов.
- •2. Принцип действия тепловой машины
- •3. Второе начало термодинамики
- •1. Энтропия
- •1. Отклонение свойств газов от идеальных.
- •2. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)
- •1. Критическое состояние вещества
- •1. Внутренняя энергия реального газа
- •1. Жидкости.
- •2. Поверхностное натяжение.
- •3. Явление смачивания.
- •4. Формула Лапласа.
- •5. Капиллярность.
3. Явление смачивания.
С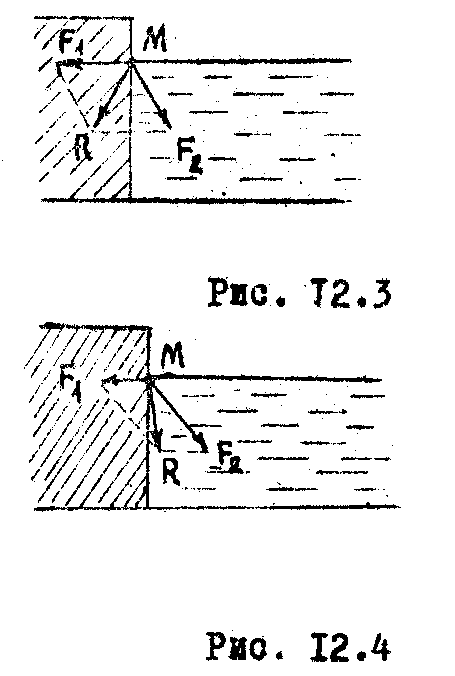 мачивание
- поверхностное явление, возникающее
при соприкосновении жидкости и твердого
тела. Оно проявляется в растекании
жидкости по твердой поверхности,
пропитывании пористых тел, образовании
мениска - искривленная поверхность
жидкости внутри узкой (капиллярной)
трубки.
мачивание
- поверхностное явление, возникающее
при соприкосновении жидкости и твердого
тела. Оно проявляется в растекании
жидкости по твердой поверхности,
пропитывании пористых тел, образовании
мениска - искривленная поверхность
жидкости внутри узкой (капиллярной)
трубки.
Н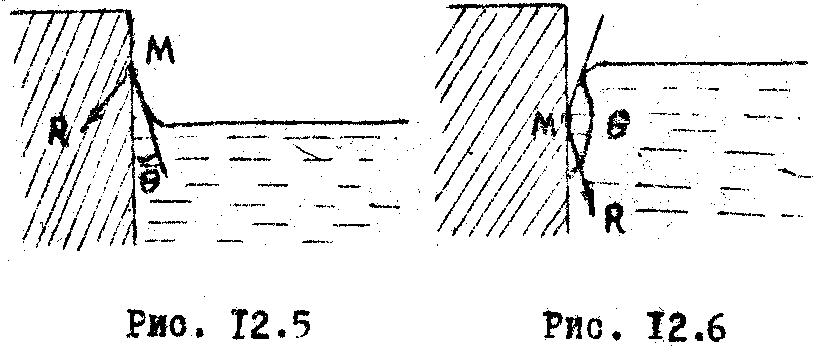 а
молекулу
,
находящуюся на поверхности жидкости,
соприкасающейся о твердым телом,
действуют молекулярные силы со стороны
твердого тела
а
молекулу
,
находящуюся на поверхности жидкости,
соприкасающейся о твердым телом,
действуют молекулярные силы со стороны
твердого тела
![]() ,
молекул жидкости
,
молекул жидкости
![]() и газа, взаимодействием с молекулами
которого можно пренебречь. В зависимости
от соотношения сил
и
их равнодействующая может быть направлена
либо в сторону твердого тела (Рис.12.3),
либо в сторону жидкости (Рис. 12.4). В первом
случае говорят, что жидкость
смачивает твердое тело.
Во втором случае жидкость не смачивает
твердое тело. При равновесии жидкости
с твердым телом ее поверхность, если
она смачивает твердое тело, несколько
приподымается, образуя вогнутый
мениск.
В другом случае поверхность жидкости
несколько опускается, образуя выпуклый
мениск (Рис.12.5,12.6). Количественной мерой
смачиваемости жидкости служит краевой
угол
и газа, взаимодействием с молекулами
которого можно пренебречь. В зависимости
от соотношения сил
и
их равнодействующая может быть направлена
либо в сторону твердого тела (Рис.12.3),
либо в сторону жидкости (Рис. 12.4). В первом
случае говорят, что жидкость
смачивает твердое тело.
Во втором случае жидкость не смачивает
твердое тело. При равновесии жидкости
с твердым телом ее поверхность, если
она смачивает твердое тело, несколько
приподымается, образуя вогнутый
мениск.
В другом случае поверхность жидкости
несколько опускается, образуя выпуклый
мениск (Рис.12.5,12.6). Количественной мерой
смачиваемости жидкости служит краевой
угол
![]() .
.
Краевым
углом
называется
угол между касательной поверхностью
жидкости и поверхностью твердого тела.
Он отсчитывается внутрь поверхности
жидкости. Если жидкость смачивает
поверхность, то
![]() ,
если же жидкость не смачивает поверхность,
то
,
если же жидкость не смачивает поверхность,
то
![]() .
.
4. Формула Лапласа.
Поверхность жидкости представляет собой как бы натянутую резиновую пленку, которая благодаря силам поверхностного натяжения стремится сократиться. Поэтому под ее искривленной поверхностью возникает добавочное давление, точно так же, как внутри резинового шара или мыльного пузыря давление на определенную величину больше давления наружного воздуха.
Для вычисления этого давления рассмотрим
шарообразную каплю жидкости радиуса
![]() .
Для изменения объема капли на
.
Для изменения объема капли на
![]() необходимо затратить работу
необходимо затратить работу
![]() ,
которая идет на изменение поверхностной
энергии
,
которая идет на изменение поверхностной
энергии
![]() .
Таким образом,
.
Таким образом,
![]() (12.5)
(12.5)
Так как для шара
![]() ,
то:
,
то:
![]()
Подставляя это в (12.5), получим:
![]() (12.6)
(12.6)
Это выражение называют формулой Лапласа, которая определяет избыточное (капиллярное) давление - положительное под выпуклой поверхностью и отрицательнее - под вогнутой.
5. Капиллярность.
Смачивание жидкостью поверхности твердого тела проявляется при движении жидкости в узких трубках - капиллярах. Если жидкость смачивает капилляр, то вследствие вогнутого мениска капиллярное давление будет приподымать уровень жидкости, и, наоборот, если жидкость не смачивает капилляр, то уровень жидкости будет опускаться. Определим высоту поднятия (опускания) жидкости. Пусть жидкость смачивает капилляр (Рис.12.7). В этом случае мениск вогнутый и капиллярное давление отрицательно. Жидкость будет подыматься, пока его давление уравновесится давлением столба жидкости:
![]()

Если
-
радиус капилляра, то радиус мениска
![]() и
и
![]() (12.7)
(12.7)
Эта формула называется законом Пюрена.
Капиллярные явления широко проявляются в природе, смачивание используется при флотации, облегчает механическую обработку металлов, влияет на моющее действие мыл.
