
- •Физические основы классической механики
- •I. Механика. Общие понятия
- •2. Кинематика точки
- •3. Скорость
- •4. Ускорение
- •5. Примеры
- •I. Основные понятия
- •2. Законы механики
- •3. Инерциальные системы отсчёта (и.С.О.)
- •4. Принципы относительности Галилея
- •5. Закон сохранения импульса
- •6. Реактивное движение
- •7. Центр инерции
- •I. Работа
- •2. Энергия
- •3. Кинетическая и потенциальная энергии
- •4. Закон сохранения механической энергии
- •5. Удар абсолютно упругих и неупругих тел
- •I. Кинематика вращательного движения
- •2. Кинетическая энергия вращательного движения. Момент инерции.
- •3. Основное уравнение динамики вращательного движения
- •4. Момент импульса. Закон сохранения момента импульса
- •I. Принцип относительности
- •2. Постулаты Эйнштейна
- •3. Преобразования Лоренца
- •4. Замедление времени
- •5. Сокращение длин
- •6. Сложение скоростей в теории относительности.
- •7. Изменение массы со скоростью
- •8. Движение релятивистской частицы
- •9. Связь между массой и энергией
- •10. Кинетическая энергия. Энергия и импульс
- •Колебания и волны
- •1. Общие сведения о колебаниях
- •2. Механические колебания
- •3. Энергия гармонических колебаний
- •1. Предмет молекулярной физики
- •2. Термодинамические параметры.
- •3. Идеальный газ
- •4. Основное уравнение мкт газов для давления.
- •5. Газовые законы как следствие молекулярно-кинетической теории.
- •1. Скорости теплового движения молекул
- •2. Распределение молекул по скоростям (Закон Максвелла)
- •3. Закон распределения Больцмана
- •4. Число столкновений и средняя длина свободного пробега молекул
- •1. Внутренняя энергия идеального газа
- •2. Первое начало термодинамики
- •3. Работа при расширении газа
- •4. Теплоемкость идеальных газов
- •5. Адиабатический процесс
- •1. Характеристика тепловых процессов.
- •2. Принцип действия тепловой машины
- •3. Второе начало термодинамики
- •1. Энтропия
- •1. Отклонение свойств газов от идеальных.
- •2. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)
- •1. Критическое состояние вещества
- •1. Внутренняя энергия реального газа
- •1. Жидкости.
- •2. Поверхностное натяжение.
- •3. Явление смачивания.
- •4. Формула Лапласа.
- •5. Капиллярность.
1. Отклонение свойств газов от идеальных.
Уравнение состояния идеального газа
(Менделеева-Клапейрона) является
приближенным. Оно выполняется при
достаточно малых плотностях и давлениях
(до 100 атм). Так, например, для одного моля
азота при
![]() С
и
С
и
![]() атм
атм
![]() отличается от теоретического более чем
на
отличается от теоретического более чем
на
![]() ,
а при
,
а при
![]() атм - на
атм - на
![]() .
При дальнейшем увеличении давления это
отклонение еще больше.
.
При дальнейшем увеличении давления это
отклонение еще больше.
Т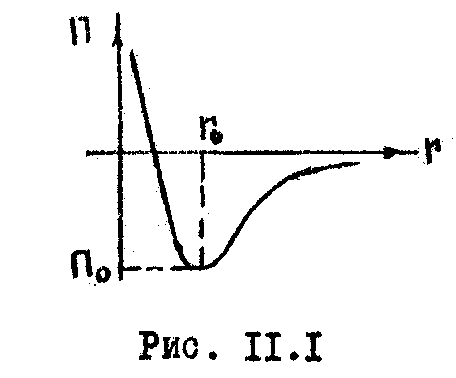 аким
образом, опыт показывает, что реальные
газы значительно отличаются по своим
свойствам от идеальных. Такие отклонения
связаны с межмолекулярным взаимодействием
и размерами самих молекул, чем нельзя
пренебрегать при больших плотностях
газа. Между молекулами действую силы
электрического происхождения -
притягивания и отталкивания. Характер
этих сил показан на рис. 11.1, где приведена
зависимость потенциальной энергии
взаимодействия от расстояния. На
расстоянии
аким
образом, опыт показывает, что реальные
газы значительно отличаются по своим
свойствам от идеальных. Такие отклонения
связаны с межмолекулярным взаимодействием
и размерами самих молекул, чем нельзя
пренебрегать при больших плотностях
газа. Между молекулами действую силы
электрического происхождения -
притягивания и отталкивания. Характер
этих сил показан на рис. 11.1, где приведена
зависимость потенциальной энергии
взаимодействия от расстояния. На
расстоянии
![]() силы притяжения уравновешиваются
силами отталкивания. Действие сил
притяжения приводит к тому, что молекулы
газа занимают определенный объем, дальше
которого газ не может быть сжат.
силы притяжения уравновешиваются
силами отталкивания. Действие сил
притяжения приводит к тому, что молекулы
газа занимают определенный объем, дальше
которого газ не может быть сжат.
Поэтому уравнение Менделеева-Клапейрона, справедливое для идеальных газов, необходимо уточнить с учетом размера молекул и сил взаимодействия между ними.
2. Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)
Для 1 моля идеального газа уравнение
состояния имеет вид
,
где
![]() -
объем, предоставленный молекулам газа.
Для реальных газов некоторая его часть
-
объем, предоставленный молекулам газа.
Для реальных газов некоторая его часть
![]() занята самими молекулами. Поэтому
объем
надо заменить разностью
занята самими молекулами. Поэтому
объем
надо заменить разностью
![]() .
.
Учтем теперь взаимодействие молекул.
Силы притяжения, действующие между
молекулами, приводят, к уменьшению
давления газа на стенки сосуда на
некоторую величину
![]() ,
так что:
,
так что:
![]() или
или![]() (11.1)
(11.1)
где
- дополнительное давление, обусловленное
силами притяжения. Его называют также
внутренним или молекулярным давлением.
Это давление пропорционально концентрации
молекул и силе, действующей на данную
молекулу со стороны остальных, которая
в свою очередь, также пропорциональна
концентрации молекул. Таким образом,
![]() или
или
![]() ,
где
- постоянная, характеризующая
силы молекулярного притяжения и
зависящая от природы газа. Таким
образом, получаем для 1 моля уравнение:
,
где
- постоянная, характеризующая
силы молекулярного притяжения и
зависящая от природы газа. Таким
образом, получаем для 1 моля уравнение:
![]() (11.2)
(11.2)
Это уравнение состояния реального газа или уравнение Ван-дер-Ваальса; и - константы, определяемые экспериментально. Исследуем уравнений (11.2), для чего перепишем его в виде:
![]() (11.3)
(11.3)
С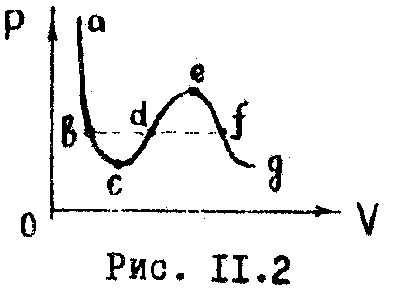 его помощью можно построить теоретические
изотермы реального газа - зависимость
его помощью можно построить теоретические
изотермы реального газа - зависимость
![]() от
при
заданных значениях
.
от
при
заданных значениях
.
У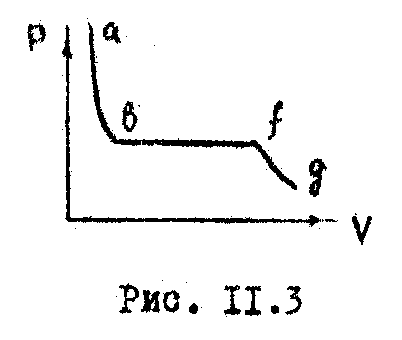 равнение
(11.3) - уравнение третьей степени
относительно
.
Поэтому оно может иметь либо три
действительных корня, либо один. Одна
из таких изотерм изображена на рис.
11.2. На участках
равнение
(11.3) - уравнение третьей степени
относительно
.
Поэтому оно может иметь либо три
действительных корня, либо один. Одна
из таких изотерм изображена на рис.
11.2. На участках
![]() ,
,![]() ,
т.е. с увеличением давления объем
уменьшается, на участке же
,
т.е. с увеличением давления объем
уменьшается, на участке же
![]() ,
что соответствует неестественному
состоянию вещества, когда сжатие приводит
к увеличению объема. Поэтому на опыта
изотерма пожег быть лишь вида
,
что соответствует неестественному
состоянию вещества, когда сжатие приводит
к увеличению объема. Поэтому на опыта
изотерма пожег быть лишь вида
![]() (Рис. 11.3). Такая изотерма действительно
была получена Т. Эндрьюсом с углекислотой.
Наличии горизонтального участка связано
с тем, что при изменении объема вещество
не может все время оставаться в однофазном
состоянии. В некоторый момент
происходит скачкообразной изменение
состояния вещества и его распадение на
две фазы: жидкую (
(Рис. 11.3). Такая изотерма действительно
была получена Т. Эндрьюсом с углекислотой.
Наличии горизонтального участка связано
с тем, что при изменении объема вещество
не может все время оставаться в однофазном
состоянии. В некоторый момент
происходит скачкообразной изменение
состояния вещества и его распадение на
две фазы: жидкую (![]() )
и газообразную (
)
и газообразную (![]() ).
Горизонтальный участок (
).
Горизонтальный участок (![]() )
соответствует двухфазному состоянию
вещества - переходу газа в жидкость
при заданных температуре и давлении.
Эта область насыщенного пара.
)
соответствует двухфазному состоянию
вещества - переходу газа в жидкость
при заданных температуре и давлении.
Эта область насыщенного пара.
Лекция 17 |
Изотермы реальных газов. Сравнение уравнения Ван-дер-Ваальса с экспериментальными данными. |
|
Фазовые переходы 1-го и 2-го рода. Критическое состояние. |
