1. Скорости теплового движения молекул

Средняя скорость молекул в газе обычно характеризуется среднеквадратичной или тепловой скоростью . Из (7.2) следует, что

(8.1)

так как ,а m - масса молекулы. Из (8.1) мож­но подсчитать, что для водорода при для кислорода и т.д.

Однако молекулы даже одного сорта газа при одних и тех те условиях имеют неодинаковые скорости. Это связано с тем, что для молекул, совершавших беспорядочное движение, все нап­равления равноправными абсолютные значения скоростей, поэтому не могут быть одинаковыми. Даже если они случайно в какой-то момент времени скорости и оказались бы одинаковыми, то в даль­нейшем такое состояние быстро бы нарушилось из-за столкновений между собой.

Благодаря беспорядочному движению и взаимным столкновени­ям молекулы газа распределяются по скоростям так, что среди них имеются как очень быстрые, так и очень медленные молекулы ( ). Такое распределение, как показывает опыт, является не случайным, а вполне определенным. На его характер не влияют ни столкновения молекул, ни внешние воздействия.

Таким образом, скорости молекул неодинаковы и подчиняются определённым закономерностям имеющим статистический характер.

2. Распределение молекул по скоростям (Закон Максвелла)

Поскольку значение скоростей молекул может быть бесконеч­но большое, а само число молекул ограниченно, то находят не число молекул, обладающих той или иной скоростью, а число молекул или их часть, обладающих скоростями, лежащими в некотором интервале вблизи заданной скорости . Например, число молекул, скорости которых лежат в пределах от 500 до 510 м/с ( ).

Относительное число молекул , скорости которых лежат в интервале , зависит од скорости V и тем больше, чем больше и , т.е.

(8.2)

ф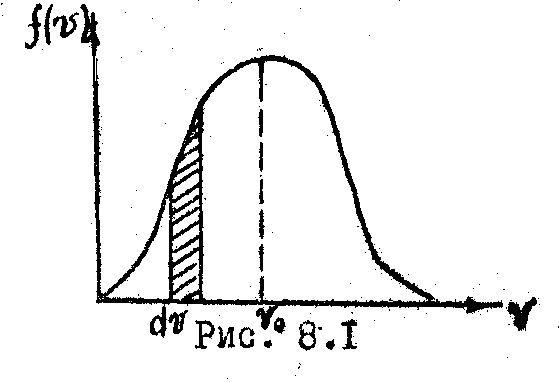 ункция называется функцией распределения. При , т.е. равна доле молекул, скорости которых заключены в единичном интервале скоростей. Так, как имеет смысл вероятности, то - вероятность того, что молекула газа имеет скорость, заключенную в единичном интервале вблизи . Можно графически представить зависимость от скорости . Число молекул , имеющих скорости , равны нулю.

Поэтому искомая зависимость, как следует из математики, должна иметь максимум при и асимптотически приближаться к оси абсцисс при (рис. 8.1). Аналитический вид ее для одинаковых молекул был рассчитан Максвеллом и. носит название закона распределения скоростей Максвелла:

(8.3)

М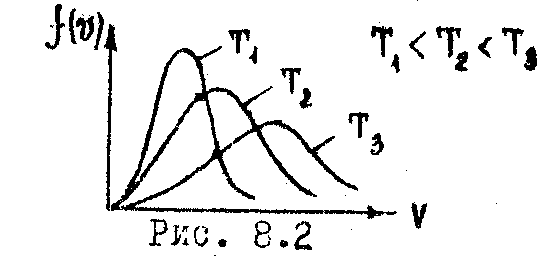 аксимум этой функции при означает, что наибольшая доля всех молекул движется со скоростями, близкими к . Эту скорость поэтому называют наивероятной скоростью. Пользуясь кривой распределения, модно найти долю молекул , имеющих скорость в заданной интервале .Она равна площади заштрихованной полосы. Вся же площадь под кривой дает полное число молекул я данном объёме. С повышением температуры скорости молекул возрастают, и кривая смещается в сторону больших скоростей (Рис. 8.2). Пользуясь (8.3) можно вычислить среднюю арифме­тическую и наивароятную ско­рость . Вычисления дают:

(8.4); (8.5)

Для решения практических задач удобно закон Максвелла (8.3) записывать через относительную скорость . Из (8.5) и (8.3) можно получить:

(8.6)

В таком виде обычно пользуются законом Максвелла для решения задач, связанных с распределением молекул по скоростям. Экспериментальная проверка формулы распределения Максвелла впервые была проведена О. Штерном в 1920 г.